Как на рисунках изображается вектор (4 видео)

Вектор: определение и основные понятия

Содержание

Определение вектора
Обозначение вектора
Длина вектора
Нулевой вектор
Коллинеарные вектора
Сонаправленные вектора
Противоположно направленные вектора
Компланарные вектора
Равные вектора
Единичный вектор
Что такое вектор: определение, обозначение, виды
Определение вектора
Виды векторов
Векторы
🔥 Видео

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Определение вектора

рис. 1

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Обозначение вектора

Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Длина вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Видео:Действия с векторами. Вектора в картинкахСкачать

Нулевой вектор

Нулевой вектор обычно обозначается как 0 .

Длина нулевого вектора равна нулю.

Видео:Трассировка. Как сделать изображение векторным? Какие картинки подойдут оптимально? Corel DrawСкачать

Коллинеарные вектора

рис. 2

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Сонаправленные вектора

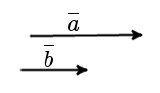рис. 3

Видео:№918. Разложите векторы а , b , с , d , е и f , изображенные на рисунке 276, а, б, вСкачать

Противоположно направленные вектора

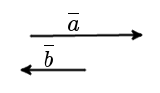рис. 4

Видео:Построение проекции вектора на осьСкачать

Компланарные вектора

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Равные вектора

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Видео:№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

Единичный вектор

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Вычитание векторов. 9 класс.Скачать

Что такое вектор: определение, обозначение, виды

В данной публикации мы рассмотрим, что такое вектор, как он обозначается, а также какие виды бывают. Теоретическую информацию сопроводим рисунками для лучшего восприятия.

Видео:№766. На рисунке 259 изображены векторы а, b , с , d , XY. Представьте вектор XYСкачать

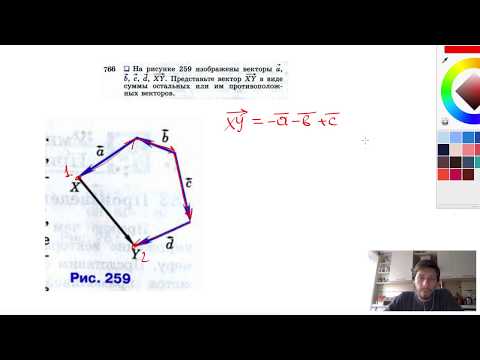
Определение вектора

Вектор – это направленный отрезок. Другими словами, это отрезок определенной длины, который направлен в конкретную сторону.

У вектора есть начало и конец. На рисунке ниже – это точки A и B, соответственно. Направление вектора показывается соответствующей стрелкой.

Обозначается вектор путем записи его точек (начало, потом – конец) с вертикальной черточкой сверху, т.е. в нашем случае – AB .

Альтернативный вариант обозначения – малеьнкая латинская буква, например, a .

Примечание: нахождение длины вектора (| AB | или | a |) мы подробно рассмотрели в отдельной публикации.

Видео:Перевод рисунка в вектор за 10 минут!Скачать

Виды векторов

1. Нулевой – начало и конец вектора совпадают. Обычно обозначается как 0 . Длина нулевого вектора равняется нулю.

2. Единичный – вектор, длина которого равна единице. Также называется ортом.

3. Коллинеарные – векторы лежат на одной и той же или на параллельных прямых.

4. Сонаправленные – коллинеарные векторы, направления которых совпадает. Например, на рисунке ниже a и b являются сонаправленными.

5. Противоположно направленные – коллинеарные векторы, направления которых противоположны.

6. Компланарные – векторы, параллельные одной плоскости или лежащие на одной плоскости.

Примечание: любые два вектора компланарны, так как всегда найдется плоскость, параллельная им обоим.

7. Равные – векторы, имеющие одинаковую длину и направление, а также лежащие на одной или параллельных прямых.

Примечание: для вектора AB в произвольной точке C пространства удастся построить только один единственный вектор (например, CD ) той же длины.

Видео:Как перевести фотографию в вектор в Adobe illustrator | Трассировка изображения в иллюстратореСкачать

Векторы

Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.

Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.

Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть (читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют равные веторы; то есть,

В контексте векторов мы применяем = чтобы обозначить их равность.

Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.

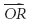
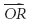
Пример 1 Векторы u, , w показаны на рисунке внизу. Докажите, что u = = w.

Решение Сначала мы находим длину каждого вектора с использованием формулы расстояния:
|u| = √ [2 — (-1)] 2 + (4 — 3) 2 = √ 9 + 1 = √ 10 ,
|| = √ [0 — (-3)] 2 + [0 — (-1)] 2 = √ 9 + 1 = √ 10 ,
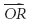
|w| = √ (4 — 1) 2 + [-1 — (-2)] 2 = √ 9 + 1 = √ 10 .
Отсюда
|u| = | 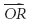= |w|.
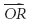
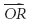
Векторы u, , и w, как видно из рисунка, вроде бы имеют одно и то же направление, но мы проверим их наклон. Если прямые, на которых они находятся, имеют одинаковые наклоны, то векторы имеют одно и то же направление. Рассчитываем наклоны:
Так как u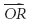, , и w имеют равные величины и одно и то же напраывление,
u = = w.

Имейте в виду, что равность векторов требует только одинаковой величины и одинакового направления, а не расположения в одном месте. На самом верхнем рисунке — пример равности векторов.

Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север. Сумма двух этих векторов есть вектор 5-ти шагов величины и в показанном направлении. Сумма также называется результирующим двух векторов.

В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.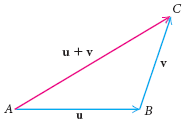

Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v. Таким образом, если u = и v = , тогда
u + v = + =

Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.

Если две силы F₁ и F₂ действуют на один объект, результирующая сила есть сумма F₁ + F₂ этих двух отдельных сил.

Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.

Решение Нарисуем условие задачи, в этом случае — прямоугольник, используя v или для представления результирующей. Чтобы найти ее величину, используем теорему Пифагора:
|v| 2 = 15 2 + 25 2 Здесь |v| обозначает длину или величину v.
|v| = √ 15 2 + 25 2
|v| ≈ 29,2.
Чтобы найти направление, отметим, что так как OAB есть прямым углом,
tanθ = 15/25 = 0,6.
Используя калькулятор, мы находим θ, угол, который большая сила образует с результирующей силой:
θ = tan — 1 (0,6) ≈ 31°
Результирующая имеет величину 29,2 и угол 31° с большей силой.

Пилоты могут корректировать направление их полёта, если есть боковой ветер. Ветер и скорость самолёта могут быть изображены как веторы.

Пример 3. Скорость самолёта и направление. Самолёт движется по азимуту 100° со скоростью 190 км/час, в то время как скорость ветра 48 км/ч, а его азимут — 220°. Найдите абсолютную скорость самолета и направление его движения с учетом ветра.

Решение Сначала сделаем рисунок. Ветер представлен и вектор скорости самолета есть . Результирующий вектор скорости есть v, сумма двух векторов. Угол θ между v и называется угол сноса.

Обратите внимание, что величина COA = 100° — 40° = 60°. Тогда величина CBA также равна 60° (противоположные углы параллклограмма равны). Так как сумма всех углов параллелограмма равна 360° и COB и OAB имеют одну и ту же величину, каждый должен быть 120°. По правилу косинусов в OAB, мы имеем
|v| 2 = 48 2 + 190 2 — 2.48.190.cos120°
|v| 2 = 47,524
|v| = 218
Тогда, |v| равно 218 км/ч. Согласно правилу синусов, в том же самом треуголнике,
48/sinθ = 218/sin120°,
или
sinθ = 48.sin120°/218 ≈ 0,1907
θ ≈ 11°
Тогда, θ = 11°, к ближайшему целому углу. Абсолютная скорость равна 218 км/ч, и направление его движения с учетом ветра: 100° — 11°, или 89°.

Если нам задан вектор w, мы можем найти два других вектора u и v, сумма которых есть w. Векторы u и v называются компонентами w и процесс их нахождения называется разложением, или представлением вектора его векторными компонентами.

Когда мы раскладываем вектор, обычно мы ищем перпендикулярные компоненты. Очень часто, однако, одна компонента будет параллельной оси x, и другая будет параллельна оси y. Поэтому, они часто называются горизонтальными и вертикальными компонентами вектора. На рисунке внизу вектор w = разложен как сумма u = и v = .

Горизонтальная компонента w есть u и вертикальная компонента — v.

Пример 4 Вектор w имеет величину 130 и наклон 40° относительно горизонтали. Разложите вектор на горизонтальные и вертикальные компоненты.

Решение Сначала мы нарисуем рисунок с горизонтальными и вертикальными векторами u и v, чья сумма есть w.

Из ABC, мы находим |u| и |v|, используя определения косинуса и синуса:
cos40° = |u|/130, или |u| = 130.cos40° ≈ 100,
sin40° = |v|/130, или |v| = 130.sin40° ≈ 84.
Тогда, горизонтальная компонента w есть 100 направо и вертикальная компонента w есть 84 вверх.