 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
- Линейная функция
- График линейной функции
- Прямые, параллельные оси ординат
- Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
- График линейной функции, его свойства и формулы
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- Докажите, что график данной функции принадлежит прямой, параллельной оси абсцисс ; найдите область определения этой функции : В)У = 3х + 4 / 5x — 10 — x — 4 / 3x — 6?
- На графике функции найти точки, в которых касательная параллельна оси абсцисс?
- Найдите абсциссу точки графика функции в которой касательная к этому графику функции параллельна прямой ( во вложении №7)?
- Докажите что график данной функции принадлежит прямой параллельной оси абсцисс найдите область определения данной фунции y = (4x — 5) / (7x — 21) — (x — 1) / (2x — 6)?
- График линейной функции — прямая, параллельная оси абсцисс и проходящая через точку M (5 ; 8)?
- Дана функция графиком которой является прямая параллельная оси абсцисс и проходящая через точку b (3 ; — 2)?
- Сделайте пожалуйста срочно ?
- Постройки график функции у = х ^ 2 — 4|х| + 3 Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
- Дана функция, графиком которой является прямая, параллельная оси абсцисс и проходящая через точку (5 ; 7)?
- Постройте график функции у = |х ^ 2 — 3х — 4| Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
- Постройке график функции у = х ^ 2 — 6|х| + 5?
Видео:Дан график производной Найти абсциссу точки в которой касательная к графику функции парал-на оси ХСкачать

Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

График линейной функции
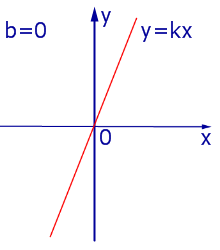
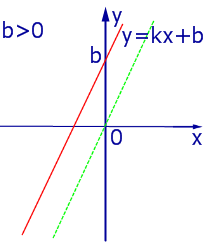
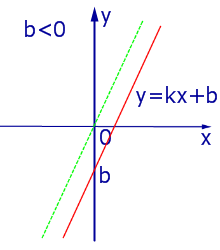
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
 |
| Рис.1 |
 |
| Рис.2 |
 |
| Рис.3 |
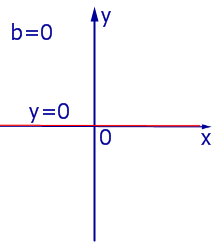
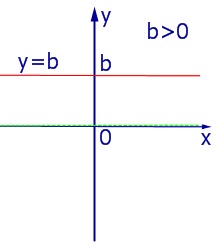
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
 |
| Рис.4 |
 |
| Рис.5 |
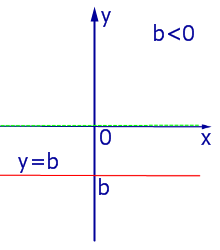 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Видео:ГРАФИК ФУНКЦИЙ — Сдвиги Графика Функции, Как строить Графики Функции // Алгебра 8 классСкачать  Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать  Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Видео:Преобразование графиков функций. y= f(x + n). Сдвиг по оси OX. 10 класс.Скачать  График линейной функции, его свойства и формулыО чем эта статья: Статья находится на проверке у методистов Skysmart. Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать  Понятие функцииФункция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции. Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек. Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать  Понятие линейной функцииЛинейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат. Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки. Если известно конкретное значение х, можно вычислить соответствующее значение у. Нам дана функция: у = 0,5х — 2. Значит:
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции. Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат. Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби. Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b». Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart! Видео:7 класс. Задайте формулой линейную функцию, параллельную данной и проходящую через точку NСкачать  Свойства линейной функции
Видео:Касательная к графику функции в точке. 10 класс.Скачать  Построение линейной функцииВ геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y. Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график: В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая. В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3). Теперь рассмотрим графики функций y = -2x + 3, y = — 1 /2x + 3, y = -x + 3. В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая. Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3). Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2. Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые. При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты. Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b. Если k 0, то график функции y = kx + b выглядит так: 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»> Если k > 0 и b > 0, то график функции y = kx + b выглядит так: 0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»> Точки пересечения графика функции y = kx + b с осями координат:
Видео:Преобразование графиков функций. Сжатие и растяжение. 10 класс.Скачать  Решение задач на линейную функциюЧтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся! Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Видео:Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать  Докажите, что график данной функции принадлежит прямой, параллельной оси абсцисс ; найдите область определения этой функции : В)У = 3х + 4 / 5x — 10 — x — 4 / 3x — 6?Алгебра | 10 — 11 классы Докажите, что график данной функции принадлежит прямой, параллельной оси абсцисс ; найдите область определения этой функции : В)У = 3х + 4 / 5x — 10 — x — 4 / 3x — 6. ОДЗфункции : взаписифункцииприсутствуютдроби, значитихзнаменателиНЕдолжныбытьравными0 : Функция Y определенанавсейчисловойпрямой, крометочких = 2. Видео:Преобразование графиков функций. y= f(x) + n. Сдвиг по оси OY. 10 класс.Скачать  На графике функции найти точки, в которых касательная параллельна оси абсцисс?На графике функции найти точки, в которых касательная параллельна оси абсцисс. Видео:Занятие 1. График линейной функции y=kx+bСкачать  Найдите абсциссу точки графика функции в которой касательная к этому графику функции параллельна прямой ( во вложении №7)?Найдите абсциссу точки графика функции в которой касательная к этому графику функции параллельна прямой ( во вложении №7). Видео:9 класс, 7 урок, Уравнение прямойСкачать  Докажите что график данной функции принадлежит прямой параллельной оси абсцисс найдите область определения данной фунции y = (4x — 5) / (7x — 21) — (x — 1) / (2x — 6)?Докажите что график данной функции принадлежит прямой параллельной оси абсцисс найдите область определения данной фунции y = (4x — 5) / (7x — 21) — (x — 1) / (2x — 6). Видео:Как построить график линейной функции.Скачать  График линейной функции — прямая, параллельная оси абсцисс и проходящая через точку M (5 ; 8)?График линейной функции — прямая, параллельная оси абсцисс и проходящая через точку M (5 ; 8). Задайте эту функцию формулой. Видео:Как построить график функции без таблицыСкачать  Дана функция графиком которой является прямая параллельная оси абсцисс и проходящая через точку b (3 ; — 2)?Дана функция графиком которой является прямая параллельная оси абсцисс и проходящая через точку b (3 ; — 2). Задайте эту функцию формулой. Видео:Формула линейной функции по ее графикуСкачать  Сделайте пожалуйста срочно ?Сделайте пожалуйста срочно ! Я вас прошу , а то у меня засада и я вообще не понимаю : ((( Докажите , что график данной функции принадлежит прямой параллельной оси абсцисс ; найдите область определения этой функции. Умоляю сделайте пожалуйста ! Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать  Постройки график функции у = х ^ 2 — 4|х| + 3 Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?Постройки график функции у = х ^ 2 — 4|х| + 3 Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс? Видео:Задание №23 ОГЭ математика 2018Скачать  Дана функция, графиком которой является прямая, параллельная оси абсцисс и проходящая через точку (5 ; 7)?Дана функция, графиком которой является прямая, параллельная оси абсцисс и проходящая через точку (5 ; 7). Задайте эту функцию формулой. Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать  Постройте график функции у = |х ^ 2 — 3х — 4| Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?Постройте график функции у = |х ^ 2 — 3х — 4| Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс? Постройке график функции у = х ^ 2 — 6|х| + 5?Постройке график функции у = х ^ 2 — 6|х| + 5. Число общих точек график данной функции может иметь с прямой , параллельной оси абсцисс? С черчежом , если можно). На этой странице вы найдете ответ на вопрос Докажите, что график данной функции принадлежит прямой, параллельной оси абсцисс ; найдите область определения этой функции : В)У = 3х + 4 / 5x — 10 — x — 4 / 3x — 6?. Вопрос соответствует категории Алгебра и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы. = 0, 25 * sin²2α вариант условия 2. Знак умножения : (1 — cos²α) * (1 + tg²α) = sin²α * (1 / cos²α) = sin²α / cos²α = (sinα / cosα)² = tg²α. Х + у = 9, у = — х + 9 2х — у = 6 у = — х + 9 2х — ( — х + 9) = 6 у = — х + 9 2х + х — 9 = 6 у = — х + 9 3х = 9 + 6 у = — х + 9 3х = 15 у = — х + 9 х = 5 у = — 5 + 9 х = 5 у = 4 х = 5 Ответ : (5 ; 4) поставь спасибо и сделай ответ лучшим. Что же вы не учите ничего? X° = — b / 2a = — 5 / ( — 4) = 1, 25 Y° = — D / 4a = — (25 + 24) / ( — 8) = 49 / 8 = 6, 125 (1, 25 ; 6, 125). . я шале плвщнавещанщавщ. 3. 83 Вот , пожалуйста тебе ответ. Рассмотрим ф — ю х² она достигает наибольшего значения при х = — 4 А = ( — 4)² = 16 у = 4х ф — я возрастающая — наименьшее ее значение при х = — 1 В = — 4 А>B. Пусть х км / ч скорость автомобиля, тогда 80 / x время затраченное им на весь путь. Оно на 20 мин = 1 / 3 часа больше времени мотоцикла. Мотоцикл проехал 3 / 2 расстояния АС. X / 3 — расстояние, на которое уехал автомобиль прежде чем выехал мотоци.. Cos 5 + cos 85 + sin 75 + sin 15 = 2, 3080953122309927549517167106643. 1 / а = 1 / b + 1 / c 1 / a = (c + b) / bc bc = a(c + b) a = bc / (c + b) Ответ : bc / (c + b). 1)m ^ — 6 * m ^ 5 = m ^ ( — 6 + 5) = m ^ — 1 / m ^ — 5 = m ^ ( — 1 — — 5) = m ^ 4 2)8a в минус 8 b8 * 7a в седьмой b в — 6 = 56a ^ — 1 b ^ 2. |

 , параллельны .
, параллельны . , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.



 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле



 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

 получаем:
получаем:

 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.




















