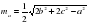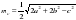Как делятся чевианы в треугольнике (4 видео)

Свойства конкурентных Чевиан треугольника

В школьном курсе геометрии я изучал только три вида отрезков в треугольнике, это медианы биссектрисы и высоты. При изучении данной проблемы я узнал, что существуют другие отрезки в треугольники — чевианы. Сразу скажем, что такое чевиана. Чевиана – это произвольный отрезок в треугольнике, исходящий из вершины к любой точке на противоположной стороне. К ним также относятся и медианы, и биссектрисы, и высоты. В свою очередь, чевианы делятся на два вида – конкурентные и неконкурентные, Конкурентные чевианы – это чевианы имеющие общую точку пересечения, а неконкурентные – это не имеющие общую точку. Нас интересуют, только конкурентные.

Каждому школьнику известно, что медиана треугольника делит его на два равновеликих треугольника, три медианы треугольника делят его на шесть равновеликих треугольников. Я заинтересовался: а будет ли это свойство выполняться для любых трех конкурентных чевиан.

1. Если чевианами являются медианы, то ответ очевиден, так как два равновеликих треугольника с общей высотой имеют равные стороны, к которым эта сторона проведена.

Правда в этом утверждении участвует много треугольников, площади которых нужно сравнивать, и возникает желание уменьшить их число. Этого можно добиться, если сначала установить следующий критерий: точка G внутри треугольника ABC принадлежит медиане AD тогда и только тогда, когда [ABG] = [CAG], где [Ф] здесь и далее обозначает площадь фигуры Ф.

Чтобы доказать это утверждение, опустим из вершин B и C треугольников ABG и CAG высоты BK и CL на прямую AD, содержащую их общую сторону AD. Нам нужно установить, что точка G принадлежит медиане AD тогда и только тогда, когда равны треугольники DBK и CLD (а они подобны при любом выборе точки G, так как прямые CL и BK перпендикулярны прямой AM и, следовательно, параллельны).

Доказанный критерий «о мотыльке с равновеликими крыльями» позволяет нам доказать, что, точка G внутри треугольника ABC является точкой пересечения медиан тогда и только тогда, когда равновеликими являются треугольники ABG. BCG и CAG.

Ясно, что если с тремя конкурентными чевианами четыре каких-то маленьких треугольника равновелики, то эти чевианы являются медианами треугольника. Достаточно ли равенства площадей трех любых таких треугольников для того, чтобы точка G оказалась точкой пересечения медиан треугольника?

Рассмотрим три случая.

1. Если три равновеликих треугольника являются соседними и, например, u = z = v, то AD – медиана треугольника ABC, так как GD медиана треугольника BGC. Но треугольник BCE составлен из трех равновеликих треугольников, и поэтому [CBG] = 2[CGE]. Но эта пара треугольников имеет общую вершину и, тем самым, одинаковые высоты. Поэтому BG = 2GE. По теореме о медианах отсюда заключаем, что G – точка пересечения медиан треугольника ABC.

2. Если только два равновеликих треугольника являются соседними (например, u = z = y), то GD – медиана треугольника GBC, то есть D – середина BC. Так как u = y, то y = w = x = u = w = x, то есть [DAB] = [EAB]. Но эта пара треугольников имеет общую сторону AB и поэтому высоты этих треугольников, к ней проведенные, равны. Таким образом, DE║AB, то есть DE – средняя линия треугольника ABC, и поэтому DE – медиана.

3. Пусть теперь у одного из «трилистников» на рис. 3 три «лопасти» равновелики: u = w = v = a. Заметим, что

[GBD]:[GDC] = BD:DC = [ABD]:[ADC], то есть

Аналогично, рассуждая, заключаем, что числа x, y, z, u, v, w удовлетворяют системе уравнений

(*) которая в рассматриваемом случае выглядит так:

Перемножая эти уравнения, имеем: xyz = a3. Сравнивая эти три пары дробей, из системы заключаем, что az + a2 = xy + ax, ax + a2 = yz + ay, ay + a2 = xz + az.

Сложим эти равенства и получим xy + xz + yz = 3a2

Умножая первое уравнение на z, второе на – x, а третье – на y, а затем, складывая полученные равенства, найдем, что a(x2 + y2 + z2) + a2(x + y + z) =

= 3xyz + a(xy + xz + yz).

Используя алгебраическое тождество x2 + y2 + z2 = (x + y+ z)2 – 2(xy +xz + yz), из последнего равенства, с учетом полученного выше равенства, заключаем, что x + y + z = 3a и тем самым числа x, y, z удовлетворяют системе уравнений x + y + z = 3a, xy + xz + yz = 3a2. xyz = a3.

Следовательно, по теореме Виета числа x, y, z являются корнями уравнения третьей степени t3 – 3at2 + 3a2t – a3 = 0, то есть уравнения (t – a)3 = 0. Отсюда уже следует, что x = y = z = a.

Что же можно утверждать, если известно, что только два из шести «маленьких треугольников» равновелики?

Решение. Рассмотрим несколько случаев.

Если u = z, то доказывать нечего, так как GD — медиана GBC.

Если u = y, то четырехугольник BDEA, как мы убедились выше, является трапецией, и поэтому прямые AC и DE параллельны. Отсюда заключаем, что CF – медиана треугольника ABC. Это следует из того, что отрезок, параллельный основаниям трапеции и проходящий через точку пересечения ее диагоналей, делится этой точкой пополам.

Наконец, если u = x, то из системы (*) легко следует, что одновременно выполняются равенства x + y + z = u + v + w, xy + yz + xz = uv + vw + uw, xyz = uvw.

Поэтому две тройки чисел (x, y, z) и (u, v, w) являются корнями одного и того же уравнения третьей степени с общим корнем x = u. Следовательно, пары чисел y, z и v, w являются корнями одного и того же квадратного уравнения.

Итак, в рассматриваемом случае возможны два варианта: x = u, y = v, z = w и x = u, y = w, z = v. Если y = v, то BE – медиана треугольника AGC и, следовательно, треугольника ABC. Если y = w и z = v, то из первых двух уравнений системы (*) получаем, что x = y = z, и тем самым, все шесть «маленьких треугольников» равновелики. Таким образом, G – точка пересечения медиан треугольника ABC, и если два равновеликих треугольника принадлежат разным «трилистникам», то одна из чевиан (по крайней мере) является медианой треугольника.

Большой интерес вызвала у меня теорема о площади треугольника, образованного тремя неконкурентными чевианами.

Теорема. Точки D, E, F делят стороны треугольника ABC так, что а чевианы AD, BE, CF пересекаются попарно в точках G, H, K

Для доказательства заметим, что для сравнения [GHK] с [ABC] достаточно сравнить каждую из площадей [AGB], [BCH], [CAK] с площадью треугольника ABC. Так как

[GHK] = [ABC] – [AGB] – [BCH] – [CAK]

Рассмотрим треугольник ABG. В четырехугольнике ABDE он является одним из четырех треугольников, на которые разбивают четырехугольник две диагонали. Для площадей таких треугольников имеет место теорема о бабочках, которая утверждает, что

1) Таким образом, все, что рассмотрено и доказано в научных трудах относится к одному виду чевиан – медианам.

2) Мне интересно найти множество точек G для трех произвольных конкурентных чевиан треугольника, для каждой точки которого площади «трилистников» равны. Для этого я провел следующие исследования:

1. Взял произвольный треугольник и провел в нем три медианы. Этот случай не требует особых измерений, так как по теореме известно, что все шесть треугольников равновелики, а значит и площади «трилистников» одинаковы.

2. Взял тот же произвольный треугольник и провел в нем высоты. В этом случае мне пришлось проводить измерения. Я измерил линейкой длины всех отрезков и вычислил площади треугольник по формуле для прямоугольных треугольников, так как чевианы являются высотами. Пришел к выводу, что площади «трилистников» не равны.

3. Вновь беру тот же произвольный треугольник и провожу в нем биссектрисы, так же измеряю длины сторон линейкой и вычисляю площади треугольников по формуле Герона , где a, b, c – стороны треугольника, а — полупериметр треугольника. И вновь прихожу к выводу, что и в этом случае площади «трилистников» не равны.

4. Беру вновь тот же треугольник и провожу в нем произвольные чевианы, вновь провожу необходимые измерения, вычисляю площади треугольников по формуле Герона. Прихожу к выводу, что и здесь площади «трилистников» не равны. Еще несколько опытов с конкурентными чевианами не изменили моего вывода.

Эти исследования убеждают меня в том, что площади «трилистников» будут равны только в том случае, когда чевианами являются медианы.

Чтобы увидеть, чем же будет являться все множество точек пересечения конкурентных чевиан, я провел следующий эксперимент: все треугольники, а во всех опытах я брал их равными и налаживал их друг на друга. Беспорядочное расположение точек пересечения конкурентных чевиан позволило мне выдвинуть гипотезу, что если построить достаточно много этих точек, то они заполнят все внутреннее пространство треугольника.

После проведенных опытов я пришел к следующим выводам:

1) Множество точек для трех произвольных конкурентных чевиан является сам треугольник, но без границ.

2) Равенство x + y + z = u + y + z имеет место только для одного вида чевиан – медиан.

В дальнейшем я хочу найти и изучить компьютерную программу, с помощью которой можно провести большое количество опытов для произвольных конкурентных чевиан.

Содержание

Длина чевианы в треугольнике
Теоремы Чевы и Менелая на ЕГЭ
Чевианы треугольника
Просмотр содержимого документа «Чевианы треугольника»
Просмотр содержимого презентации «Чевианы треугольника»
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
💥 Видео

Видео:Теорема Менелая | Математика | TutorOnlineСкачать

Длина чевианы в треугольнике

Видео:Теорема ЧевыСкачать

Теоремы Чевы и Менелая на ЕГЭ

Теоремы Чевы и Менелая на ЕГЭ

Подробная статья «Вокруг теорем Чевы и Менелая» опубликована на нашем сайте в разделе СТАТЬИ. Она адресована учителям математики и учащимся старших классов, мотивированным на хорошее знание математики. К ней можно вернуться, если появится желание подробнее разобраться в вопросе. В этой заметке мы приведем краткие сведения из упомянутой статьи и разберём решения задач из сборника для подготовки к ЕГЭ-2016.

Пусть дан треугольник ABC и на его сторонах AB, BC и AC отмечены точки C1, A1 и B1 соответственно (рис. 1).

а) Если отрезки AА1, BB1 и CС1 пересекаются в одной точке, то

. (1)

б) Если верно равенство (1), то отрезки AА1, BB1 и CС1 пересекаются в одной точке.

На рисунке 1 изображен случай, когда отрезки AА1, BB1 и CС1 пересекаются в одной точке внутри треугольника. Это так называемый случай внутренней точки. Теорема Чевы справедлива и в случае внешней точки, когда одна из точек А1, B1 или С1 принадлежит стороне треугольника, а две другие — продолжениям сторон треугольника. В этом случае точка пересечения отрезков AА1, BB1 и CС1 лежит вне треугольника (рис. 2).

Как запомнить равенство Чевы?

Обратим внимание на прием запоминания равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC, начиная с точки A. От точки A идем к точке B, встречаем точку С1, записываем дробь . Далее от точки В идем к точке С, встречаем точку А1, записываем дробь . Наконец, от точки С идем к точке А, встречаем точку В1, записываем дробь . В случае внешней точки порядок записи дробей сохраняется, хотя две «точки деления» отрезка оказываются вне своих отрезков. В таких случаях говорят, что точка делит отрезок внешним образом.

Отметим, что любой отрезок, соединяющий вершину треугольника с любой точкой прямой, содержащей противоположную сторону треугольника, называют чевианой.

Рассмотрим несколько способов доказательства утверждения а) теоремы Чевы для случая внутренней точки. Чтобы доказать теорему Чевы, надо доказать утверждение а) любым из предложенных ниже способов, а также доказать утверждение б). Доказательство утверждения б) приведено после первого способа доказательства утверждения а). Доказательства теоремы Чевы для случая внешней точки проводятся аналогично.

Доказательство утверждения а) теоремы Чевы с помощью теоремы о пропорциональных отрезках

Пусть три чевианы AA1, BB1 и CC1 пересекаются в точке Z внутри треугольника ABC.

Идея доказательства заключается в том, чтобы отношения отрезков из равенства (1) заменить отношениями отрезков, лежащих на одной прямой.

Через точку В проведем прямую, параллельную чевиане СС1. Прямая АА1 пересекает построенную прямую в точке М, а прямая, проходящая через точку C и параллельная АА1, — в точке Т. Через точки А и С проведем прямые, параллельные чевиане ВВ1. Они пересекут прямую ВМ в точках N и R соответственно (рис. 3).

По теореме о пропорциональных отрезках имеем:

, и .

Тогда справедливы равенства

В параллелограммах ZСTM и ZСRВ отрезки TM, СZ и ВR равны как противоположные стороны параллелограмма. Следовательно, и верно равенство

Утверждение а) теоремы Чевы доказано.

При доказательстве утверждения б) используем следующее утверждение. Рис. 3

Лемма 1. Если точки С1 и С2 делят отрезок AB внутренним (или внешним) образом в одном и том же отношении, считая от одной и той же точки, то эти точки совпадают.

Докажем лемму для случая, когда точки С1 и С2 делят отрезок AB внутренним образом в одном и том же отношении: .

Доказательство. Из равенства следуют равенства и . Последнее из них выполняется лишь при условии, что С1B и С2B равны, т. е. при условии, что точки С1 и С2 совпадают.

Доказательство леммы для случая, когда точки С1 и С2 делят отрезок AB внешним образом проводится аналогично.

Доказательство утверждения б) теоремы Чевы

Пусть теперь верно равенство (1). Докажем, что отрезки AА1, BB1 и CС1 пересекаются в одной точке.

Пусть чевианы АА1 и ВВ1 пересекаются в точке Z, проведем через эту точку отрезок CС2 (С2 лежит на отрезке AB). Тогда на основании утверждения а) получаем верное равенство

. (2)

Из сравнения равенств (1) и (2) заключаем, что , т. е. точки С1 и С2 делят отрезок AB в одном и том же отношении, считая от одной и той же точки. Из леммы 1 следует, что точки С1 и С2 совпадают. Это означает, что отрезки AА1, BB1 и CС1 пересекаются в одной точке, что и требовалось доказать.

Можно доказать, что процедура записи равенства (1) не зависит, от того, от какой точки и в каком направлении совершается обход вершин треугольника.

Задание 1. Найдите длину отрезка АN на рисунке 4, на котором указаны длины других отрезков.

Задание 2. Чевианы AM, BN, CK пересекаются в одной точке внутри треугольника ABC. Найдите отношение , если , . Рис. 4

Ответ. .

Доказательство утверждения а) с помощью подобия треугольников

Приведем доказательство теоремы Чевы из статьи [1]. Идея доказательства заключается в том, чтобы заменить отношения отрезков из равенства (1) отношениями отрезков, лежащих на параллельных прямых.

Пусть прямые AA1, BB1, CC1 пересекаются в точке O внутри треугольника АВС (рис. 5). Через вершину С треугольника АВС проведем прямую, параллельную AB, и ее точки пересечения с прямыми AA1, BB1 обозначим соответственно A2, B2.

Из подобия двух пар треугольников CB2B1 и ABB1, BAA1 и CA2A1, Рис. 5

, . (3)

Из подобия треугольников BС1O и B2CO, AС1O и A2CO имеем равенства , из которых следует, что

. (4)

Перемножив равенства (3) и (4), получим равенство (1).

Утверждение а) теоремы Чевы доказано.

Рассмотрим доказательства утверждения а) теоремы Чевы с помощью площадей для внутренней точки. Оно изложено в книге [2] и опирается на утверждения, которые мы сформулируем в виде заданий 3 и 4.

Задание 3. Отношение площадей двух треугольников с общей вершиной и основаниями, лежащими на одной прямой, равно отношению длин этих оснований. Докажите это утверждение.

Задание 4. Докажите, что если , то и . Рис. 6

Доказательство утверждения а) с помощью площадей

Пусть отрезки AА1, BB1 и CС1 пересекаются в точке Z (рис. 6), тогда

, . (5)

Из равенств (5) и второго утверждения задания 4 следует, что или . Аналогично получим, что и . Перемножив три последние равенства, получим:

т. е. верно равенство (1), что и требовалось доказать.

Утверждение а) теоремы Чевы доказано.

Задание 15. Пусть чевианы пересекаются в одной точке внутри треугольника и разбивают его на 6 треугольников, площади которых равны S1, S2, S3, S4, S5, S6 (рис. 7). Докажите, что . Рис. 7

Задание 6. Найдите площадь S треугольника CNZ (площади других треугольников указаны на рисунке 8).

Задание 7. Найдите площадь S треугольника CNO, если площадь треугольника АNO равна 10 и , (рис. 9).

Задание 8. Найдите площадь S треугольника CNO, если площадь треугольника АBC равна 88 и , (рис. 9).

Решение. Так как , то обозначим, . Так как , то обозначим , . Из теоремы Чевы следует, что , и тогда . Если , то (рис. 10). У нас три неизвестные величины (x, y и S), поэтому для нахождения S составим три уравнения.

Так как , то = 88. Так как , то , откуда . Так как , то .

Итак, , откуда . Рис. 10

Задание 9. В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и BC. , . P — точка пересечения отрезков AL и CK. Площадь треугольника PBC равна 1. Найдите площадь треугольника ABC.

Теорема Менелая

Пусть дан треугольник ABC и на его сторонах AC и CВ отмечены точки B1 и A1 соответственно, а на продолжении стороны AB отмечена точка C1 (рис. 11).

а) Если точки А1, B1 и С1 лежат на одной прямой, то

. (6)

б) Если верно равенство (7), то точки А1, B1 и С1 лежат на одной прямой. Рис. 11

Как запомнить равенство Менелая?

Прием запоминания равенства (6) тот же, что и для равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC — от вершины к вершине, проходя через точки деления (внутренние или внешние).

Задание 10. Докажите, что при записи равенства (6) от любой вершины треугольника в любом направлении получается один и тот же результат.

Чтобы доказать теорему Менелая, надо доказать утверждение а) любым из предложенных ниже способов, а также доказать утверждение б). Доказательство утверждения б) приведено после первого способа доказательства утверждения а).

Доказательство утверждения а) с помощью теоремы о пропорциональных отрезках

I способ. а) Идея доказательства заключается в замене отношений длин отрезков в равенстве (6) отношениями длин отрезков, лежащих на одной прямой.

Пусть точки А1, B1 и С1 лежат на одной прямой. Через точку C проведем прямую l, параллельную прямой А1B1, она пересекает прямую АB в точке M (рис. 12).

По теореме о пропорциональных отрезках имеем: и .

Тогда верны равенства .

Утверждение а) теоремы Менелая доказано.

Доказательство утверждения б) теоремы Менелая

Пусть теперь верно равенство (6), докажем, что точки А1, B1 и С1 лежат на одной прямой. Пусть прямые АB и А1B1 пересекаются в точке С2 (рис. 13).

Так как точки А1 B1 и С2 лежат на одной прямой, то по утверждению а) теоремы Менелая

. (7)

Из сравнения равенств (6) и (7) имеем , откуда следует, что верны равенства

, , .

Последнее равенство верно лишь при условии , т. е. если точки С1 и С2 совпадают.

Утверждение б) теоремы Менелая доказано. Рис. 13

Доказательство утверждения а) с помощью подобия треугольников

Идея доказательства заключается в том, чтобы заменить отношения длин отрезков из равенства (6) отношениями длин отрезков, лежащих на параллельных прямых.

Пусть точки А1, B1 и С1 лежат на одной прямой. Из точек A, B и C проведем перпендикуляры АА0, BB0 и СС0 к этой прямой (рис. 14).

Из подобия трех пар треугольников AA0B1 и CC0B1, CC0A1 и BB0A1, C1B0B и C1A0A (по двум углам) имеем верные равенства

, , ,

перемножив их, получим:

Утверждение а) теоремы Менелая доказано.

Доказательство утверждения а) с помощью площадей

Идея доказательства заключается в замене отношения длин отрезков из равенства (7) отношениями площадей треугольников.

Пусть точки А1, B1 и С1 лежат на одной прямой. Соединим точки C и C1. Обозначим площади треугольников S1, S2, S3, S4, S5 (рис. 15).

Тогда справедливы равенства

, , . (8)

Перемножив равенства (8), получим:

Утверждение а) теоремы Менелая доказано.

Подобно тому, как теорема Чевы остается справедливой и в том случае, если точка пересечения чевиан находится вне треугольника, теорема Менелая остается справедливой и в том случае, если секущая пересекает только продолжения сторон треугольника. В этом случае можно говорить о пересечении сторон треугольника во внешних точках.

Доказательство утверждения а) для случая внешних точек

Пусть секущая пересекает стороны треугольника ABC во внешних точках, т. е. пересекает продолжения сторон AB, BC и AC в точках C1, A1 и B1 соответственно и эти точки лежат на одной прямой (рис. 16).

По теореме о пропорциональных отрезках имеем:

и .

Тогда верны равенства

Утверждение а) теоремы Менелая доказано. Рис. 16

Заметим, что приведенное доказательство совпадает с доказательством теоремы Менелая для случая, когда секущая пересекает две стороны треугольника во внутренних точках и одну во внешней.

Доказательство утверждения б) теоремы Менелая для случая внешних точек аналогично доказательству, приведенному выше.

Задание 11. В треугольнике АВС точки А1, В1 лежат соответственно на сторонах ВС и AС. P — точка пересечения отрезков АА1 и ВВ1. , . Найдите отношение .

Решение. Обозначим , , , (рис. 17). По теореме Менелая для треугольника BCВ1 и секущей PA1 запишем верное равенство:

откуда следует, что

. Рис. 17

Ответ. .

Задание 12 (МГУ, заочные подготовительные курсы). В треугольнике АВС, площадь которого равна 6, на стороне АВ взята точка К, делящая эту сторону в отношении , а на стороне АС — точка L, делящая АС в отношении . Точка P пересечения прямых СК и ВL удалена от прямой АВ на расстояние 1,5. Найдите длину стороны АВ.

Решение. Из точек Р и С опустим перпендикуляры PR и СМ на прямую АВ. Обозначим , , , (рис. 18). По теореме Менелая для треугольника AKC и секущей PL запишем верное равенство: , откуда получим, что , . Рис. 18

Из подобия треугольников КMC и КRP (по двум углам) получим, что , откуда следует, что .

Теперь, зная длину высоты, проведенной к стороне AB треугольника ABС, и площадь этого треугольника, вычислим длину стороны: .

Задание 13. Три окружности с центрами А, В, С, радиусы которых относятся как , касаются друг друга внешним образом в точках X, Y, Z как показано на рисунке 19. Отрезки AX и BY пересекаются в точке O. В каком отношении, считая от точки B, отрезок CZ делит отрезок BY?

Решение. Обозначим , , (рис. 19). Так как , то по утверждению б) теоремы Чевы отрезки АX, BY и СZ пересекаются в одной точке — точке O. Тогда отрезок CZ делит отрезок BY в отношении . Найдем это отношение. Рис. 19

По теореме Менелая для треугольника BCY и секущей OX имеем: , откуда следует, что .

Ответ. .

Задание 14 (ЕГЭ-2016).

Точки В1 и С1 лежат на сторонах соответственно АС и АВ треугольника ABC, причём АВ1:B1С =
= АС1:С1B. Прямые ВВ1 и СС1 пересекаются в точке О.

а) Докажите, что прямая АО делит пополам сторону ВС.

б) Найдите отношение площади четырёхугольника AB1OC1 к площади треугольника ABC, если известно, что АВ1:B1С = 1:4. [8]

Решение. а) Пусть прямая AO пересекает сторону BC в точке A1 (рис. 20). По теореме Чевы имеем:

. (9)

Так как АВ1:B1С = АС1:С1B, то из равенства (9) следует, что , то есть CA1 = А1B, что и требовалось доказать. Рис. 20

б) Пусть площадь треугольника AB1O равна S. Так как АВ1:B1С = 1:4, то площадь треугольника CB1O равна 4S, а площадь треугольника AOC равна 5S. Тогда площадь треугольника AOB тоже равна 5S, так как треугольники AOB и AOC имеют общее основание AO, а их вершины B и C равноудалены от прямой AO. Причём площадь треугольника AOC1 равна S, так как АС1:С1B = 1:4. Тогда площадь треугольника ABB1 равна 6S. Так как АВ1:B1С = 1:4, то площадь треугольника CB1O равна 24S, а площадь треугольника ABC равна 30S. Теперь найдём отношение площади четырёхугольника AB1OC1 (2S) к площади треугольника ABC (30S), оно равно 1:15.

Задание 15 (ЕГЭ-2016).

а) Докажите, что прямая АО делит пополам сторону ВС.

б) Найдите отношение площади четырёхугольника AB1OC1 к площади треугольника ABC, если известно, что АВ1:B1С = 1:3. [8]

Задание 16 (ЕГЭ-2016). На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием ВС является боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что cosABC = . В каком отношении прямая DL делит сторону АВ? [8]

Решение. а) Пусть углы при основании BC равнобедренного треугольника ABC (рис. 21) равны , так как BL биссектриса ABC, то LBC = . Он равен углу LDB при основании BD равнобедренного треугольника BLD. Тогда внешний угол LCB треугольника DCL равен , а внутренний угол LDC, не смежный с ним, равен . Из свойства внешнего угла треугольника следует, что другой внутренний угол треугольника DCL равен – = , то есть треугольник DCL равнобедренный (DC = CL), что и требовалось доказать. Рис. 21

б) Пусть AK — медиана, проведённая к основанию BC равнобедренного треугольника ABC, она является высотой, поэтому BK:BA = cosABC = . Обозначим BK = x, тогда BC = 2x, BA = BС = 6x. Биссектриса BL делит сторону BС в отношении CL:LA = BC:BA = 1:3. Тогда CL = CD = = 1,5x.

По теореме Менелая , откуда, учитывая, что CL = CD, имеем: = .

Задание 17 (ЕГЭ-2016). На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием ВС является боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что cosABC = . В каком отношении прямая DL делит сторону АВ? [8]

1. , Смирнов точки и линии треугольника. М.: Математика, 2006, № 17.

2. Мякишев геометрии треугольника. (Серия «Библиотека «Математическое просвещение»»). М.: МЦНМО, 2002. — 32 с.

3. Геометрия. Дополнительные главы к учебнику 8 класса: Учебное пособие для учащихся школ и классов с углубленным изучением / , , и др. — М.: Вита-Пресс, 2005. — 208 с.

4. Теоремы Чевы и Менелая. М.: Квант, 1990, № 3, С. 56–59.

5. Шарыгин Чевы и Менелая. М.: Квант, 1976, № 11, С. 22–30.

6. Вавилов и средние линии треугольника. М.: Математика, 2006, № 1.

7. Ефремов Дм. Новая геометрия треугольника. Одесса, 1902. — 334 с.

8. Математика. 50 вариантов типовых тестовых заданий / , , и др.; под ред. . – М.: Издательство «Экзамен», 2016. — 247 с.

Видео:✓ Теорема Чевы | Осторожно, спойлер! | Борис ТрушинСкачать

Чевианы треугольника

Данная разработка — конспект факультативного занятия по теме «Чевианы треугольника» с презентацией. Цель занятия — систематизация знаний и введение дополнительных сведений о медианах, высотах и биссектрисах треугольника, применение полученных знаний для решения задач повышенной сложности, предлагаемых на ГИА и ЕГЭ.

Просмотр содержимого документа
«Чевианы треугольника»

Внеклассное мероприятие для учащихся 9-10 классов в рамках подготовки к ГИА и ЕГЭ

Софронова Н.А., учитель математики МОУ «Упшинская ООШ» Оршанского района РМЭ

Форма проведения – факультативное занятие

Обучающая: Систематизация знаний и введение дополнительных сведений о медианах, высотах и биссектрисах треугольника.

Развивающая: Применение полученных знаний для решения задач повышенной сложности.

Воспитательная: Формирование культуры умственного труда и интереса к предмету, установки на самообразование, коммуникабельности.

Презентация к уроку

Раздаточный материал: тексты задач, справочная информация

Комментарии к слайду

1. Организационный момент

Меня зовут Н.А. Я – учитель математики УООШ.

Сегодня, в рамках подготовки к ЕГЭ, мы поговорим о самой замечательной, на мой взгляд, геометрической фигуре – треугольнике.

Тема нашего занятия – ЧЕВИАНЫ ТРЕУГОЛЬНИКА. Я не буду объяснять вам значение слова ЧЕВИАНА. Я предполагаю, что к концу этого урока вы сами дадите ему толкование.

Эпиграф к уроку: «Три пути ведут к знанию: путь размышлений – самый благодарный, путь подражания – самый легкий и путь опыта – это путь самый горький.» (Конфуций)

Пусть этот час будет для вас дорогой размышления, приобретения нового опыта и использования старого с новых позиций.

Работа с презентацией.

2. Актуализация знаний

Итак – главный герой нашего занятия – треугольник. А что это такое? Перед вами несколько высказываний о треугольнике. Какое из них можно считать определением треугольника?

Треугольник – это фигура, состоящая из трех точек

Треугольник – это фигура, состоящая из трех отрезков

Треугольник – это фигура, состоящая из трех углов

Треугольник – это фигура, состоящая из трех точек и трех отрезков, соединяющих эти точки.

Работа с презентацией.

Каков правильный ответ?

На слайде нет верного определения треугольника.

Треугольник – это фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.

Для понимания материала сегодняшнего занятия повторим метрические соотношения в треугольнике. А чтобы процесс повторения не был скучным, проведем его в виде игры «Банкиры».

В ходе игры участвуют две команды, каждая из которых представляет правление банка. Игроки выбирают президента банка. Президент от имени правления отвечает на предложенные в ходе игры задания различной стоимости (либо посоветовавшись с правлением, либо самостоятельно), тем самым увеличивая активы своего банка.

Банки – конкурирующие организации. У банков общая денежная единица — 1 «ум». У каждого банка – начальный стартовый капитал – 5 «умов».

Командам предлагаются по очереди задания различной стоимости. Если команда дает правильный ответ, то ее стартовый капитал увеличивается на стоимость задания. В противном случае – капитал уменьшается на стоимость задания, если на предложенный вопрос ответила другая команда и на половину стоимости задания, если на предложенный вопрос никто не ответил.

А сейчас проведем отборочный тур с целью выяснить, какая из команд начнет игру первой.

Работа с презентацией.

Раздать листочек со словами: ВД – это ….

Допустимы сокращения слова вплоть до одной буквы. Скорость и правильность .

Задание отборочного тура

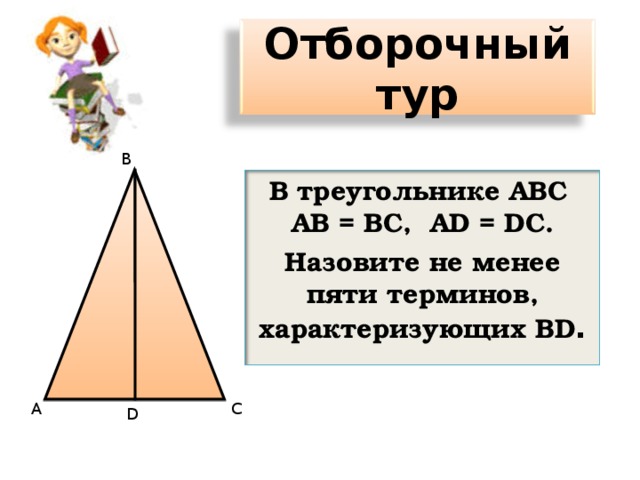
Напишите не менее пяти терминов, характеризующих В D .

Работа с презентацией.

P . S . Если количество ответов совпадает – жеребьевка (орел, решка)

высота, ось симметрии, ГМТ, равноудал. от А и С,

сер перпендикуляр к АС, чевиана, недиана,

Задание 1 стоимостью в 1 ум

Исключи лишнее слово в классификации треугольников

А. Остроугольные Б. Равнобедренные

В. Прямоугольные Г. Тупоугольные

Работа с презентацией.

Задание 2 стоимостью в 1 ум

Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны —

А. высота Б. би ссектриса В. ср. линия Г. медиана

Работа с презентацией.

У вас есть возможность заработать еще по 1 «уму», если вы ответите на вопросы: что такое высота, медиана, биссектриса треугольн.

Б. – это отрезок биссектрисы угла тр-ка, соединяющий вершину с точкой противоположной стороны.

В. – перпендикуляр, проведенный из вершины к прямой, содерж, прот. стор.

Задание 3 стоимостью в 2 ума

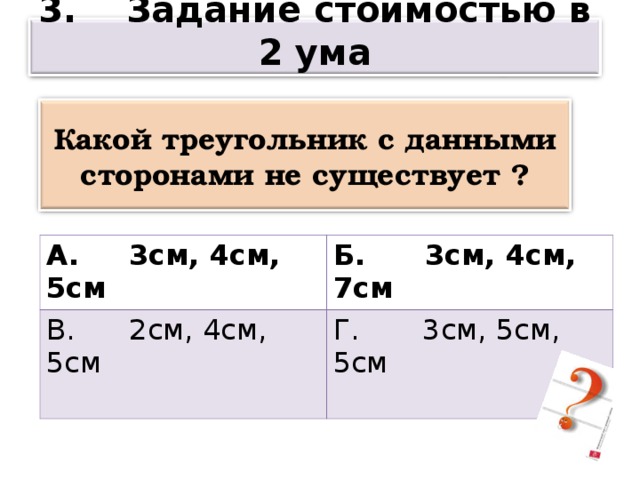
Какой треугольник с данными сторонами не существует ?

Работа с презентацией.

Напомнить неравенство треугольника

Задание 4 стоимостью в 2 ума

Какие числа соответствуют сторонам египетского треугольника?

А. 10, 15, 20 Б. 7, 8, 11

Работа с презентацией.

Уточнить, как по длинам сторон определить вид треугольника

Задание 5 стоимостью в 3 ума

Для треугольника АВС справедливо равенство:

Теорема косинусов для ВС

Работа с презентацией.

Дополнительный вопрос на 1 «ум» о нахождении углов по теореме косинусов.

Задание 6 стоимостью в 3 ума

По теореме синусов

А. стороны треугольника обр. пропор синусам противолеж углов

Б. стороны треугольника пропорцион синусам прилежащих углов

В. стороны треугольника пропорцион синусам противол. углов

Г. стороны треугольника обр. пропорц. синусам прилежащ углов

Работа с презенацией.

Задание 7 стоимостью в 3 ума

Какая из приведенных ниже формул не является формулой для нахождения площади треугольника?

Работа с презентацией.

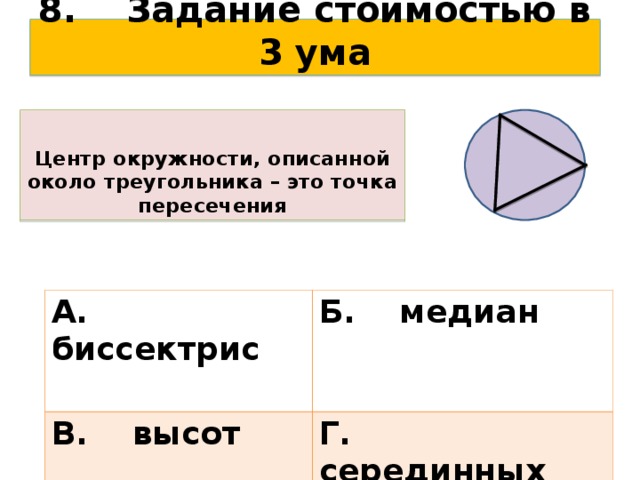
Задание 8 стоимостью в 3 ума

Центр окружности, описанной около треугольника – это точка пересечения

Г. серединных перпендикуляров

Работа с презентацией.

Уточнить: точка пересечения биссектрис – центр вписанной окр.

Дополнительные вопросы на 1 «ум»

Какими свойствами обладают медианы и биссектрисы треугольника?

Задание 9 стоимостью в 4 ума

Кто открыл формулу Герона?

«Метрика» ( Μετρική ) Герона — справочник по прикладной математике. Среди содержащихся в «Метрике» сведений: Формула Герона для расчёта площади треугольника по длинам его сторон, открытая Архимедом

Работа с презентацией.

Ответ: Б (Архимед)

Задание 10 стоимостью в 4 ума

Кто автор изречения: «Природа говорит языком математики, буквы этого языка – круги, треугольники и иные математические фигуры» ?

Работа с презентацией.

3. Постановка целей урока

Итак, в ходе игры мы повторили материал, относящийся к решению треугольников.

Однако при решении многих задач на «треугольник» этих знаний бывает недостаточно. Полезно взять на вооружение еще несколько формул на количественные соотношения в треугольнике, связанные с медианами, высотами и биссектрисами треугольника, а также формулы для вычисления их длин высот, медиан и биссектрис.

Раздать справочный материал по треугольнику

4.1. Свойства медианы треугольника

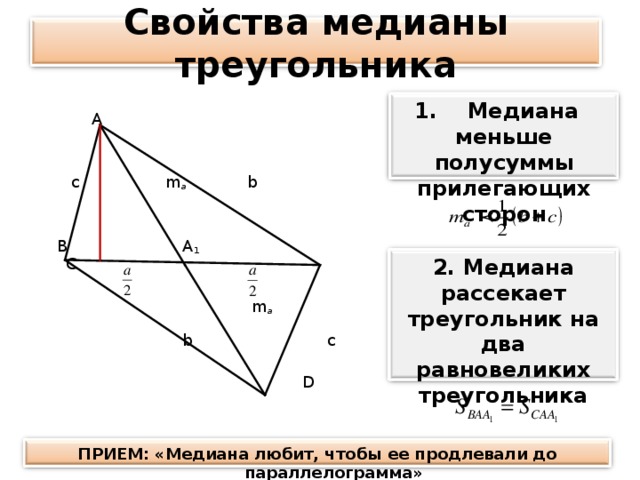
Свойства медианы треугольника

Медиана меньше полусуммы прилегающих сторон.

Медиана рассекает треугольник на два равновеликих треугольника

Работа с презентацией.

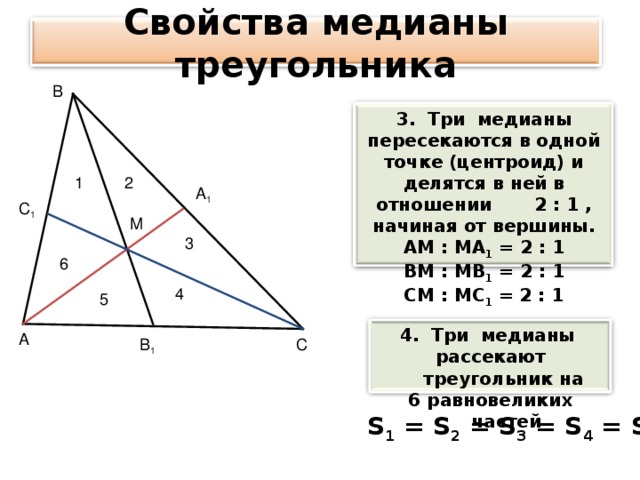
Три медианы пересекаются в одной точке и делятся в ней в отношении 2 : 1 , начиная от вершины.

Три медианы рассекают треугольник на

6 равновеликих частей

Работа с презентацией.

Задача: Медианы треугольника равны 9 см, 12 см и 15 см.

Найти отрезки, на которые они делятся точкой пересечения

2ч + 1 ч = 9 6 см и 3 см

2ч + 1 ч = 9 8 см и 4 см

2ч + 1 ч = 9 10 см и 5 см

Решение задач на свойства медианы

Дан треугольник АВ C со сторонами ВС = а, АС = b , АВ = c . Найти медиану, проведенную к стороне ВС

Работа с презентацией.

Совместный вывод формулы

У учеников РАЗДАТОЧНЫЙ МАТЕРИАЛ:

Записывают вывод формулы длины медианы

Дан треугольник АВ C со сторонами ВС = 9, АС = 7, АВ = 8. Найти медиану, проведенную к стороне АВ

АВ = с Найти m _c

Работа с презентацией.

Решают предложенные задачи: Задача 2.

АВ = с Найти m _c

Записывают формулу для m _c

Медианы треугольника равны 9, 12 и 15. Найдите площадь треугольника.

Основание треугольника равно 20 см, медианы боковых сторон равны 24 и 18 см. Найти площадь треугольника

Порекомендовать самостоятельно решить задачу 4 (д/з)

Реш.ение задачи 3.

Прием – до парал.ВАСД

Стороны тр. ВМД – 6,8 и 10 , он прямоугольн., Его площадь 24 см 2

Площадь тр. ВМА₁ — 12

Площадь тр.АВС — 72

Свойства биссектрисы треугольника

Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам.

ВЕ – биссектриса. АЕ:ЕС = ВА : ВС

Найти отрезки, на которые биссектриса угла В треугольника АВС делит сторону АС, если а = 6,

Ответ: 4 см и 3 см

Работа с презентацией.

Вспоминаем еще раз свойства биссектрис треугольника

Три биссектрисы треугольника пересекаются в одной точке, называемой инцентром.

Точка пересечения биссектрис является центром вписанной в треугольник окружности.

ВЕ – биссектриса. АЕ:ЕС = ВА : ВС

Записывают реш. зад 5

Вывод формулы длины биссектрисы

Вывод формулы длины биссектрисы (план)

Работа с презентацией.

Составить формулы для двух других биссектрис

Работа с презентацией.

Вернуться к слайду 19

Проверить формулу для задачи 5

В треугольнике PQR длина биссектрисы РО равна 6, отношение длин отрезков QO и OR равно 3:4, периметр треугольника PQR равен 21. Чему равен косинус угла QPR ?

Работа с презентацией.

В треугольнике АВС длина стороны АВ равна 18, длина биссектрисы АЕ равна 4√15, а длина отрезка ЕС равна 5.

Определите периметр треугольника АВС.

предложить решить самостоятельно

Итоги соревнований банков

И еще мне хочется вернуться к словам великого Конфуция относительно дорог к знаниям и услышать от вас

Каков был ваш путь к знаниям на сегодняшнем занятии: подражания, опята или размышления?

Работа с презентацией.

Весь урок говорили о медианах, биссектрисах. К сожалению, время не позволило нам поговорить о высотах треугольника.

Почему же тема нашего мероприятия — ЧЕВИАНЫ ТРЕУГОЛЬНИКА?

Чевиана – это отрезок, соединяющий вершину и точку на противоположной стороне.

Просмотр содержимого презентации
«Чевианы треугольника»

Три пути ведут к знанию:

путь подражания – самый легкий

и путь опыта – это путь самый горький.

Треугольник – это фигура, состоящая из трех точек.
Треугольник – это фигура, состоящая из трех отрезков.
Треугольник – это фигура, состоящая из трех углов.
Треугольник – это фигура, состоящая из трех точек и трех отрезков, соединяющих эти точки.
Треугольник – это фигура, состоящая из трех точек,не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.

В ходе игры участвуют две команды, каждая из которых представляет правление банка. Игроки выбирают президента банка. Президент от имени правления отвечает на предложенные в ходе игры задания (либо посоветовавшись с правлением, либо самостоятельно).
Банки – конкурирующие организации. У банков общая денежная единица — 1 «ум». У каждого банка – начальный стартовый капитал – 5 «умов».
Командам предлагаются по очереди задания различной стоимости. Если команда дает правильный ответ, то ее стартовый капитал увеличивается на стоимость задания . В противном случае – капитал уменьшается на стоимость задания, если на предложенный вопрос ответила другая команда и на половину стоимости задания, если на предложенный вопрос никто не ответил.

Назовите не менее пяти терминов, характеризующих В D .

1. Задание стоимостью в 1 ум

Исключи лишнее слово в классификации треугольников

2. Задание стоимостью в 1 ум

Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны —

3. Задание стоимостью в 2 ума

Какой треугольник с данными сторонами не существует ?

4. Задание стоимостью в 2 ума

Какие числа соответствуют сторонам египетского треугольника?

5. Задание стоимостью в 3 ума

Для треугольника АВС справедливо равенство:

6. Задание стоимостью в 3 ума

По теореме синусов

А. стороны треугольника обратно пропорциональны синусам противолежащих углов

Б. стороны треугольника пропорциональны синусам прилежащих углов

В. стороны треугольника пропорциональны синусам противолежащих углов

Г. стороны треугольника обратно пропорциональны синусам прилежащих углов

7. Задание стоимостью в 3 ума

Какая из приведенных ниже формул не является формулой для нахождения площади треугольника?

8. Задание стоимостью в 3 ума

Центр окружности, описанной около треугольника – это точка пересечения

Г. серединных перпендикуляров

9. Задание стоимостью в 4 ума

Кто открыл формулу Герона?

8. Задание стоимостью в 3 ума

10. Задание стоимостью в 4 ума

Свойства медианы треугольника

меньше полусуммы прилегающих сторон

2. Медиана рассекает треугольник на два равновеликих треугольника

ПРИЕМ: «Медиана любит, чтобы ее продлевали до параллелограмма»

Свойства медианы треугольника

3. Три медианы пересекаются в одной точке (центроид) и делятся в ней в отношении 2 : 1 , начиная от вершины.

Видео:Чевианы треугольника и поиск площадейСкачать

Please wait.

Видео:Теорема ЧевыСкачать

We are checking your browser. mathvox.ru

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d8901e02c0116c7 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Please wait.

Видео:Олимпиадная задача за 2 минуты ➜ Найдите уголСкачать

We are checking your browser. mathvox.ru

Видео:Вписанная окружность делит чевиану пополам. ЗАДАЧА - БЛЕСК!Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Формулы для медианы треугольникаСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6dbdcf85b9413a83 • Your IP : 85.95.188.35 • Performance & security by Cloudflare