Сумма углов треугольника римана (5 видео)

Геометрия Римана

В 1846 году Риман Георг Фридрих Бернхард поступил в Гёттингенский университет. Юный студент слушал лекции выдающегося немецкого математика Карла Гаусса. В Берлинском университете Бернхард Риман посещает лекции К. Якоби по механике и П. Дирихле по теории чисел. Знания полученных от этих гениальных ученых впоследствии будут развиты Риманом. В Гёттингенском университете Риман сотрудничал с талантливым физиком В. Вебером. Благодаря Веберу Риман заинтересовался проблемами математического естествознания. В 1851 Риман защитил докторскую диссертацию «Основы общей теории функций одной комплексной переменной». В 1857 становится профессором Гёттингенского университета. Лекции профессора Римана легли в основу ряда новых курсов таких, как математической физики, теории тяготения, электричества и магнетизма, эллиптических функций.

Научно-исследовательские труды Бернхард Римана оказали огромное влияние на развитие математики в конце XIX и начале XX веков.

Уже в докторской диссертации Риманом были заложены основы геометрического направления теории аналитических функций. Выдающийся математик и геометр Риман ввел так называемые римановы поверхности, которые сыграли важную роль при исследовании многозначных функций. Более того, им была разработана теория конформных отображений, а также представлены основные идеи топологии, изучены условия существования аналитических функций внутри областей различного вида и многое другое.

Методы, разработанные Риманом нашли широкое применение в теории алгебраических функций и интегралов, по аналитической теории дифференциальных уравнений, в частности, уравнений, определяющих гипергеометрические функции, по аналитической теории чисел. К примеру, Риманом была указана связь распределения простых чисел со свойствами дзета-функции, а именно: с распределением её нулей в комплексной области — так называемая гипотеза Римана, однако ее справедливость ещё не доказана

В 1854 году в своей знаменитой лекции «О гипотезах, лежащих в основании геометрии» Риман дал общую идею математического пространства или «многообразия», включая функциональные и топологические пространства. Здесь Риман рассматривал геометрию как учение о непрерывных n-мерных многообразиях, то есть совокупностях любых однородных объектов. Обобщив результаты К. Гаусса по внутренней геометрии поверхностей, Риман сформулировал понятие линейного элемента, так называемого дифференциала расстояния между точками многообразия. Главным достижением ученого Римана стало создание новой геометрии.

Риманова геометрия — это раздел дифференциальной геометрии, объектом изучения которой, главным образом, являются римановы многообразия . Римановы многообразия — это гладкие многообразия с дополнительной структурой, римановой метрикой, то есть с выбором евклидовой метрики на каждом касательном пространстве, которая гладко меняется от точки к точке.

Подразделом римановой геометрии является геометрия в целом, которая выявляет связь глобальных свойств риманова многообразия (к примеру, топология или диаметр) и его локальных свойств (к примеру, ограничений на кривизну).

Основными элементами трехмерной римановой геометрии являются точки, прямые и плоскости.

В римановой геометрии имеют место такие предложения: через каждые две точки проходит одна прямая, каждые две плоскости пересекаются по одной прямой, каждые две прямые, лежащие в одной плоскости, пересекаются (в одной точке), точки на прямой расположены в циклическом порядке (как и прямые, лежащие в одной плоскости и проходящие через одну точку). Таким образом, требования аксиом римановой геометрии, относящиеся конгруэнтности, обеспечивают свободные движения фигур по плоскости и в пространстве Римана, как на плоскости, так и в пространстве Евклида.

Метрические свойства плоскости Римана «в малом» совпадают с метрическими свойствами обыкновенной сферы, а именно: для любой точки плоскости Римана существует содержащая эту точку часть плоскости, изометричная некоторой части сферы; радиус R этой сферы — один и тот же для всех плоскостей данного пространства Римана. Число К = 1/R 2 называется кривизной пространства Римана. Следует отметить, что, чем меньше К , тем ближе свойства фигур этого пространства к евклидовым.

«В целом» свойства плоскости Римана отличаются от свойств целой сферы в следующем: на плоскости Римана две прямые пересекаются в одной точке, а на сфере два больших круга, которые выступают как прямые в сферической геометрии, пересекаются в двух точках; прямая, лежащая на плоскости, не разделяет эту плоскость, таким образом, если прямая а лежит в плоскости a, то любые две точки плоскости a, не лежащие на прямой а , возможно соединить отрезком, не пересекая прямой а .

Таким образом, Риман построил вторую разновидность неевклидовой геометрии в противоположность геометрии Лобачевского.

Уникальные идеи и методы, предложенные Риманом открыли новые пути для развития математики и нашли применение в механике и физике. Развитию римановой геометрии послужило создание итальянскими учеными Риччи-Курбастро и Леви-Чивита тензорного исчисления.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Сумма углов треугольника римана

Во всей истории науки нет ничего более революционного, чем развитие неевклидовых геометрий, которое до основания потрясло веру в то, что теория Евклида является вечной истиной.

Эдвард Каснер и Джеймс Ньюмен («Математика и воображение», 1941)

Все мы знаем множество геометрических понятий, потому что постоянно используем этот раздел математики в нашей повседневной жизни. Но эти понятия относятся к так называемой «классической», или «евклидовой», геометрии. Однако существуют другие геометрии, которые устроены совсем не так, как нас учили в школе. Эта книга не сделает вас специалистом в нетрадиционных геометриях, зато покажет, что реальность гораздо богаче, чем кажется на первый взгляд.

В этой книге описаны другие способы мышления и отношения к геометрии, способы, отличающиеся от тех, которые прочно укоренились в нашей повседневной жизни, и которые определяют наши действия в соответствии с евклидовой геометрией. Можно подумать, что новые геометрии понятны лишь великим ученым, но мы постараемся в последующих главах в наиболее ясной и понятной форме изложить их основы.

Возможно, самым простым способом открытия новых миров является попытка увидеть их проявления в более понятных и очевидных сферах нашей повседневной жизни. Таким образом, наше изложение начнется с короткого путешествия в «геометрию такси», которая основана на так называемом «расстоянии Минковского», отличающемся от расстояния в обычном понимании. Как бы мы ни хотели улететь в дальние экзотические страны, для начала мы должны не терять землю под ногами. Нам придется обратиться к Евклиду, чтобы понять, как основные элементы геометрии используются в повседневной жизни. Лишь тогда мы сможем перейти к обсуждению таких понятий, как «пятый постулат» и «проблема параллелей», из которых рождаются интересующие нас новые геометрии.

Лишь владея лучшими инструментами математической теории, мы можем вступить в мир новых геометрий. Сначала проведем разведку, чтобы узнать, как обстоят дела. Мы рассмотрим различные попытки доказательства пятого постулата. Ведь только в XVIII в. непоколебимое на протяжении столетий учение Евклида было наконец поставлено под сомнение самыми выдающимися математиками того времени.

Неудачные попытки доказать пятый постулат поставили под сомнение, казалось бы, неоспоримые основы традиционной геометрии. В это время и проявили себя одни из самых замечательных ученых в области математики. История альтернативных интерпретаций пятого постулата является в равной мере историей неудач и гениальных открытий. С ней связаны самые известные в истории математики имена: Лобачевский, Бойяи, Гаусс, Риман… Мы более подробно рассмотрим удивительные результаты первой из новых геометрий — гиперболической геометрии Лобачевского и Бойяи. Мы увидим, как она кардинально изменила наше понимание физической реальности и как она повлияла на исследования Альберта Эйнштейна и открытие им теории относительности.

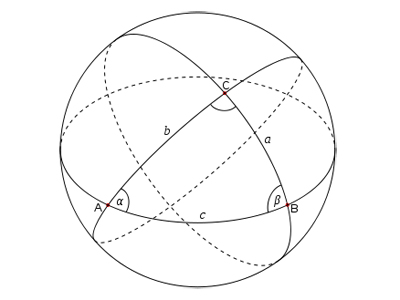
Эллиптическая геометрия Римана перенесет нас в удивительный мир сфер, где у треугольников сумма внутренних углов больше 180°. Мы воспользуемся сферической геометрией, чтобы ответить на многие вопросы. Что является кратчайшим расстоянием между двумя городами на поверхности Земли? Можно ли измерить внутренние углы треугольника, вершинами которого являются Париж, Лондон и Мадрид? Решения этих геометрических задач оказываются весьма полезными в нашем глобализованном мире, где GPS позволяет определить координаты любой точки нашей планеты.

Словно река, прорвавшая древнюю плотину, новые идеи смели традиционные научные понятия и породили сотни новых. Мы коснемся также геометрии XXI в. — интегральной и вычислительной геометрии, являющейся основой новых технологий.

Читатели, желающие поглубже изучить эти вопросы, найдут в конце книги список литературы. Алфавитный указатель позволит легко ориентироваться в тексте книги.

Поездка на такси

Нам часто приходится в повседневной жизни измерять предметы. Математическую дисциплину, изучающую такие задачи, древние греки называли геометрией. Это слово происходит от греческого geometrein, где geo означает «земля», a metrein — «измерять». Когда мы говорим о геометрии, мы всегда используем единственное число.

Казалось бы, множественное число — геометрии — подразумевает существование целого ряда возможных дисциплин на выбор. Такой подход звучит слишком заумно, эта идея находится за пределами понимания обычных людей. Тем не менее, так оно и есть: другие геометрии существуют.

Разве ученые абсолютно точно знают, что такое на самом деле точка в пространстве или прямая линия, проходящая через нее? Может ли круг иметь форму прямоугольника? Знаем ли мы, что означает «параллельность»?

Ответы на эти вопросы не являются вечными истинами, а меняются на протяжении времени. Евклид с полной убежденностью утверждал, что «через точку вне прямой можно провести только одну прямую, параллельную данной», но Лобачевский показал, что можно провести много параллельных прямых, практически бесконечное число. Риман был не согласен с обоими и считал, что параллельные прямые не существуют. Кто же из этих великих математиков прав? Может, все они правы?

Или они все ошибаются?

В данной главе мы как раз и разрешим все эти неопределенности, но, пожалуй, нам лучше начать с простого примера, который наглядно демонстрирует, почему возникает путаница относительно самой природы физической реальности.

Отправляясь из дома на работу или в другое место, мы вычисляем время, которое потребуется на дорогу, исходя из расстояния. Но часто оказывается, что расчеты не соответствуют реальному времени. Пробки, светофоры, дорожные работы — список таких задержек можно продолжать бесконечно. Все это, казалось бы, идет наперекор нашим тщательным планам.

Проблема заключается в том, что мысленно мы моделируем наше путешествие геометрически идеальным образом, представляя наш путь в виде почти прямой линии. Однако реальность вовсе не является геометрически идеальной. Наши расчеты нарушают не только неисправные светофоры или разгружающие товары грузовики. Дело еще и в том, что блоки городских зданий не образуют идеальных квадратов, а улицы не пересекаются под идеально прямыми углами… Означает ли это, что невозможно найти оптимальную дорогу, чтобы утром добраться до работы?

ИЛЬДЕФОНСО СЕРДА (1815–1876)

Известный главным образом как инженер и архитектор, Ильдефонсо Серда обладал многими талантами, занимаясь также экономикой, правом и политикой. Его реформа городского планирования в Барселоне в XIX в., получившая название «План Серда», изменила лицо города, в результате чего появился один из самых впечатляющих районов — Эшампле. По-каталонски (I’Eixample) или по-испански (el Ensanche) это означает «расширение». Улицы Эшампле образуют прямоугольные кварталы, пересекаясь на равных расстояниях друг от друга.

Вид с воздуха на район Эшампле в Барселоне.

Как и следовало ожидать, реальность никогда не бывает геометрически идеальной, иначе бы мир был очень скучным, представляя из себя утомительные повторения упорядоченных форм. Однако рациональность и упорядоченность являются важными критериями, которые необходимо учитывать на практике, например, в городском планировании. По вполне разумным причинам улицы многих современных городов образуют квадратные блоки. Одним из первых примеров такого городского планирования был район Эшампле в испанском городе Барселоне, детище архитектора Ильдефонсо Серда. Этот район послужит идеальным вводным примером к нашей теме.

Видео:Сумма углов треугольникаСкачать

РИ́МАНОВА ГЕОМЕ́ТРИЯ

В книжной версии

Том 28. Москва, 2015, стр. 518-519

Скопировать библиографическую ссылку:

РИ́МАНОВА ГЕОМЕ́ТРИЯ, многомерное обобщение геометрии на поверхности, представляющее собой теорию римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка по сравнению с размером области). Р. г. получила своё назв. по имени Б. Римана , заложившего её основы в 1854.