Найти площадь заштрихованного треугольника

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Видео:Задача на 5 секунд. Найти площадь заштрихованной фигурыСкачать

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Видео:Найти площадь заштрихованной фигуры.Скачать

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Видео:Найдите площадь закрашенной фигуры ★ 2 способа решения ★ Задание 3 ЕГЭ профильСкачать

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Видео:Как найти площадь закрашенной фигуры? Несложная геометрическая задачаСкачать

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Если известна сторона и высота

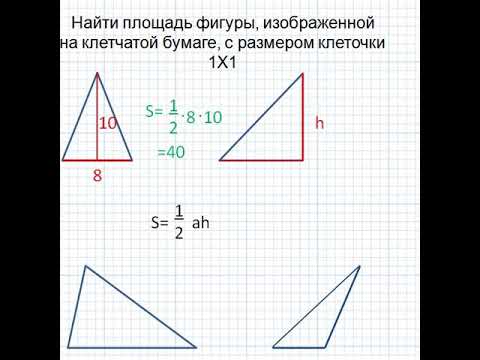
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Видео:Найти площадь заштрихованной областиСкачать

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Видео:Задача Свободы Найти площадь заштрихованной фигурыСкачать

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Видео:Как найти площадь фигуры?Скачать

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Видео:Найдите площадь заштрихованного треугольника. DTM тесты.Скачать

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

Видео:Площадь фигурыСкачать

Круг на клетчатой бумаге

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Так как центральный угол, соответствующий данному сектору, равен 90º, то

2) На клетчатой бумаге изображён круг.

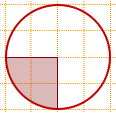
Какова площадь круга, если площадь заштрихованного сектора равна 17?

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

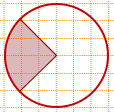
Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

5) На клетчатой бумаге изображен круг площадью 96.

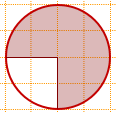
Найдите площадь заштрихованного сектора.

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

Рассмотрим треугольник ABC.

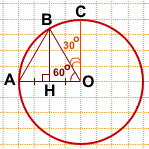
Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

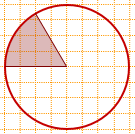
Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

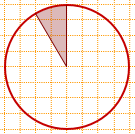
Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

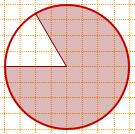
Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) Центральный угол равен 30+45=75°,

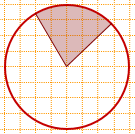
площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

10) Центральный угол равен 180-30=150°,

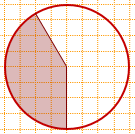
площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

11) Центральный угол равен 60-45=15°,

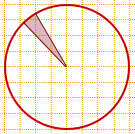
площадь заштрихованного сектора составляет 1/24 площади круга

12) Центральный угол равен 15+90=105°

📺 Видео

@Площадь заштрихованного треугольника найти #геометрияСкачать

Как найти площадь треугольника без формулы?Скачать

Как найти площадь закрашенного треугольника?Скачать

№1128. Сторона квадрата на рисунке 317 равна а. Вычислите площадь закрашенной фигуры.Скачать

Площади треугольникаСкачать

На клетчатой бумаге изображены два круга. Найдите площадь заштрихованной фигуры.Скачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Как найти площадь этого треугольника, не зная формулы?Скачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

Хитрая олимпиадная задача про полосатый треугольникСкачать