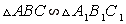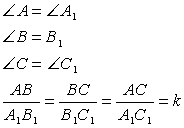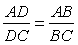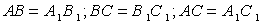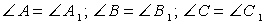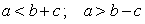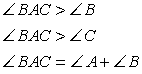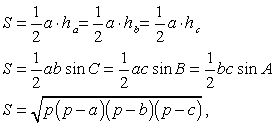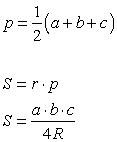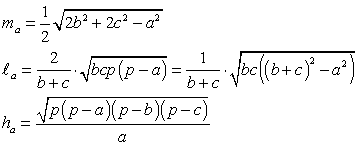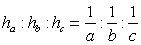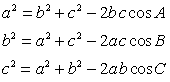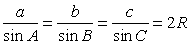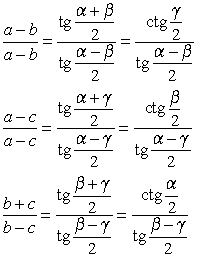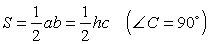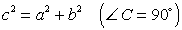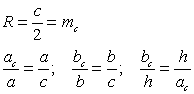Что значит треугольники пропорциональны

Видео:8 класс, 19 урок, Пропорциональные отрезкиСкачать

Определение

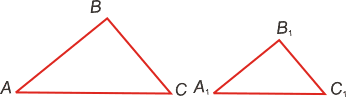
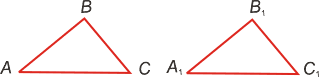
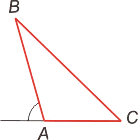
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Свойства подобных треугольников

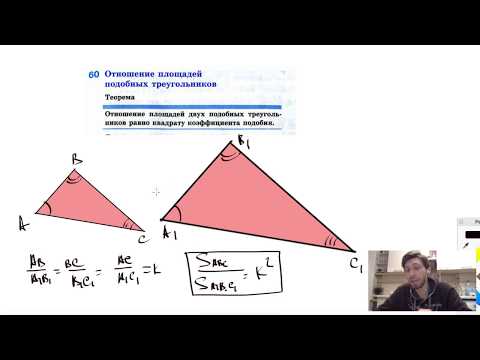
• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
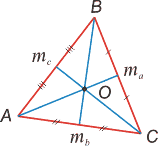
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Геометрия

План урока:

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Пропорциональные отрезки

Если известна длина двух отрезков, то можно узнать, во сколько раз один из них больше другого. Например, если некоторый отрезок NM = 24 см, а другой отрезок KP = 4 см, то можно утверждать, что NM в 6 раз длиннее, так как

Величину NM/KP именуют отношением отрезков NM и KP. Надо заметить, что в ряде случаев отношение отрезков можно найти, не зная их длины. Пусть в ∆МКР проведена медиана МН. Очевидно, что отрезок КР будет вдвое длиннее КН, ведь Н – середина КР:

Другой пример – это отношение между диагональю квадрата и его стороной.

Используя теорему Пифагора, несложно показать, что в любом квадрате АВСD

Наконец, в прямоугольном треуг-ке, один из углов которого равен 30°, гипотенуза всегда вдвое длиннее меньшего из катетов:

Если отношение отрезка AB к А₁В₁ равно отношению отрезка СD к С₁D₁, то говорят, что отрезки AB и CD пропорциональны отрезкам А₁В₁ и С₁D₁. Например, пусть

Получается, AВ и CD пропорциональны А₁В₁ и С₁D₁. Важно отметить, что пропорциональны могут быть также сразу три и более отрезка.

Видео:Прямо пропорциональная и обратно пропорциональная зависимость. 6 класс.Скачать

Определение подобных треугольников

В жизни нередко можно наблюдать объекты, у которых совпадает форма, но отличаются размеры. В качестве примера можно привести мяч для настольного тенниса и баскетбольный мяч. Оба этих предмета имеют форму шара, на баскетбольный мяч значительно больше. Другой пример – настоящий танк и игрушка, изображающая его. Часто подобны друг другу матрешки, которые вкладываются друг в друга – все они выглядят одинаково, а отличаются только общим размером. Наконец, подобны и знаменитые египетские пирамиды:

Такие объекты в геометрии именуют подобными. Подобны друг другу любые две окружности и любые два квадрата. Но особо важную роль в геометрии играют подобные треугольники. Рассмотрим это понятие подробнее.

Пусть есть два треуг-ка, ∆AВС и ∆А₁В₁С₁, у которых соответственно равны углы:

Стороны, которые лежат против одинаковых углов в таких треуг-ках, именуют сходственными. Ими являются стороны AВ и А₁В₁, ВС и В₁С₁, АС и А₁С₁.

Можно дать такое определение подобных треугольников:

Таким образом, подобие треугольников (оно обозначается символом ∾) обозначает выполнение сразу нескольких равенств:

Отношение между сходственными сторонами подобных треуг-ков именуется коэффициентом подобия и обозначается буквой k:

Грубо говоря, подобие треуг-ков означает, что их форма одинакова, но один из них в несколько раз больше или меньше другого. Чтобы получить, из одного треуг-ка другой, равный ему по размерам, его надо просто «масштабировать». Например, на этом рисунке все стороны исходного треуг-ка просто увеличили в три раза:

Это значит, что коэффициент подобия в данном случае равен 3. Однако важно понимать, что в различных геометрических задачах подобные треуг-ки также могут быть повернуты друг относительно друга:

Задание. ∆AВС подобен ∆DEF. Известно, что

Найдите длину ЕF.

Решение. Как только в задаче появляются подобные треуг-ки, стоит сразу же определить их коэффициент подобия, а для этого надо разобраться, какие стороны будут сходственными. Так как∠А = ∠Е, то лежащие против них стороны DF и ВС– сходственные. Их отношение и будет равно коэффициенту подобия:

Получили, что стороны ∆DEF вдвое длиннее сходственных им сторон ∆AВС. У подобных треуг-ков углы одинаковы, поэтому∠С = ∠D. Отсюда следует, что стороны AВ и ЕF сходственны, а потому ЕF вдвое больше:

Задание. ∆AВС и∆DEF – подобные. Известно, что

Найдите длину ЕF.

Решение. По сравнению с предыдущей задачей изменилось только одно условие, теперь∠А = ∠D. Однако это меняет сходственные стороны. Из подобия треуг-ков следует, что∠С = ∠Е. Тогда сходственными оказываются уже стороны AВ и DF. Найдем коэффициент подобия треугольников:

Сходственными являются также стороны ВС и ЕF (ведь∠А = ∠D), поэтому ЕF в 1,25 раза длиннее:

Эти две задачи показывают, как важно правильно определять сходственные стороны подобных треугольников.

Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице.

Задание. Докажите, что у подобных треуг-ков отношение их периметров равно коэффициенту подобия.

Решение. Пусть подобны ∆ AВС и ∆А₁В₁С₁, причем

Периметр ∆AВС можно вычислить так:

Мы доказали утверждение, сформулированное в условии.

Видео:ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Первый признак подобия треугольников

Оказывается, для того, чтобы доказать подобие треуг-ков, не требуется сравнивать все их углы и находить соотношение всех сторон. Существуют три простых признака подобия треугольников.

Однако прежде, чем сформулировать их, нам придется доказать отдельное утверждение, которое известно как обобщенная теорема Фалеса («обычную», не обобщенную теорему мы уже изучали ранее).

Если прямые ВВ₁ и СС₁ (показаны красным цветом)параллельны, то отрезки AВ и АС пропорциональны отрезкам AВ₁ и АС₁, то есть справедливо соотношение:

Доказывать будем от противного. Пусть отрезки AВ и АС непропорциональны AВ₁ и АС₁. Тогда отметим наАС такую точку Н, которая разобьет АС на пропорциональные отрезки, то есть

Естественно, эта точка не будет совпадать с С₁. Рассмотрим случай, когда она окажется правее, чем С₁:

Теперь поступим следующим образом. Проведем через стороны угла большое число прямых, параллельных ВС, которые будут разбивать АС на одинаковые отрезки. По теореме Фалеса эти же прямые отсекут одинаковые отрезки и на AВ. При этом мы проведем настолько много параллельных прямых, что хотя бы одна из них пересечет отрезок С₁Н:

Пусть эта прямая пересечет отрезок С₁Н в некоторой точке С₂, а сторону AВ в точке В₂. Ясно, что отрезки AВ и АВ₂ пропорциональны отрезкам АС и АС₂, так как они состоят из одинакового количества одинаковых отрезков. Например, на построенном рисунке отношение AB₂ к AB равно 5/8, так как AB₂ состоит из 5 отрезков, отсеченных зелеными параллельными прямыми, а AB состоит из 8 таких отрезков. Аналогично и отношение АС₂ к АС также равно 5 к 8. Таким образом, можно записать:

Здесь мы рассмотрели случай, когда точка Н лежит правее С₁, то есть АН >C₁. Случай, когда АН 2 раз. Докажем это.

Пусть ∆AВС и ∆А₁В₁С₁ подобны с коэффициентом подобия k. Снова проведем в них высоты СН и СН₁:

Запишем очевидные равенства:

В итоге получили, что площади подобных треугольников отличаются в k 2 раз.

Задание. Известно, у ∆AВС площадь составляет 10, а отрезок AВ имеет длину 5. ∆DEF подобен ∆AВС, причем сторона DE, сходственная AВ, равна 15. Вычислите площадь ∆DEF.

Решение. По условию задачи легко найти коэффициент подобия ∆AВС и ∆DEF, надо лишь поделить одну сходственную сторону на другую:

Задание. Площади двух подобных треуг-ков составляют 75 м 2 и 300 м 2 . Одна из сторон второго треуг-ка равна 9 м. Вычислите сходственную ей сторону первого треуг-ка.

Решение. Зная площади треуг-ков, легко найдем коэффициент их подобия:

Если коэффициент равен 2, то стороны первого многоугольника вдвое меньше сторон второго, поэтому интересующая нас сторона равна

Видео:60. Отношение площадей подобных треугольниковСкачать

Что значит треугольники пропорциональны

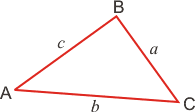
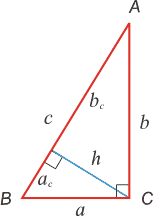
Обозначения:

А, В, С — вершины, а также углы при этих вершинах;

а, b, с — стороны, противолежащие углам
А, В, С соответственно;

h_a , h_b , h_c — высоты, опущенные на стороны

а, b, с соответственно;

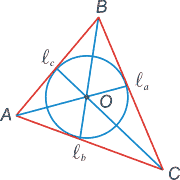
R — радиус описанной окружности;

r — радиус вписанной окружности.

Подобие треугольников

Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого треугольника.

Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого и углы, образованные этими сторонами в этих треугольниках, равны.

Два треугольника подобны, если три стороны одного треугольника пропорциональны сторонам другого треугольника.

Прямоугольные треугольники подобны,
если гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.

Если треугольники подобны, то

Пропорциональные отрезки в треугольнике

Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника:

Высотой треугольника
называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение.

Высоты треугольника пересекаются в одной точке О, называемой ортоцентром.

В тупоугольном треугольнике ортоцентр лежит вне треугольника.
В прямоугольном он совпадает с вершиной прямого угла.

Медианой треугольника
называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны.

Медианы треугольника пересекаются в одной точке О, являющейся центром тяжести треугольника.

Точкой О медианы делятся на отрезки в отношении 2: 1 (считая от вершины).

Биссектрисой треугольника
называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной.

Биссектрисой угла называется луч, делящий угол пополам.

Биссектрисы треугольника пересекаются в одной точке, являющейся центром впмсанной окружности.

Признак 1

Признак 2

Признак 3

Равенство треугольников Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны. Два треугольника называются равными, если при наложении друг на друга они совместятся. Неавенства треугольника Всякая сторона треугольника меньше суммы и больше разности двух сторон Внешний угол треугольника больше любого внутреннего угла, не смежного с ним. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Площадь треугольника где р — полупериметр треугольника (формула Герона). Прямоугольный треугольник Теорема Пифагора Равносторонний треугольник 💥 Видео 8 класс, 20 урок, Определение подобных треугольниковСкачать Масштаб. 6 класс.Скачать ПОДОБНЫЕ ТРЕУГОЛЬНИКИ . §12 геометрия 8 классСкачать ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать Теорема Пуанкаре-Перельмана простыми словами – математик Алексей Савватеев | НаучпопСкачать Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать Подобные треугольники - 8 класс геометрияСкачать Геометрия Второй признак подобия треугольников Если две стороны одного треугольника пропорциональныСкачать Что такое подобные треугольники (similar triangles). Коэф подобия (scale factor). Признаки. (8-9 кл)Скачать Основная теорема о пропорциональностиСкачать 8 класс, 24 урок, Третий признак подобия треугольниковСкачать Поделиться или сохранить к себе: Смотрите также Площадь равнобедренного треугольника Площадь прямоугольного треугольника Плечо силы в треугольнике Плетение треугольника мозаичным плетением Плетение треугольника из лозы Плетение треугольника из веревки Плетение из газетных трубочек треугольник Плетение из бисера треугольник Признак 1 Признак 2 Признак 3 то соответственные стороны и соответственные углы равны Медиана, биссектриса, высота Высоты и стороны треугольника Теорема косинусов Теорема синусов Теорема тангенсов