Расстояние от прямой до плоскости если прямая параллельна плоскости то

В этой статье дано определение расстояния между параллельными прямой и плоскостью, приведена теория, необходимая для нахождения расстояния между прямой и параллельной ей плоскостью методом координат, а также подробно разобраны решения характерных примеров и задач.

Навигация по странице.

Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Расстояние между параллельными прямой и плоскостью – определение.

Расстояние между прямой и параллельной ей плоскостью определяется через расстояние от точки до плоскости.

Расстояние между параллельными прямой и плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.

Рассмотрим прямую a и параллельную ей плоскость . Отметим на прямой a точку M₁ и опустим перпендикуляр M₁H₁ из этой точки на плоскость . Длина перпендикуляра M₁H₁ есть расстояние между заданными параллельными прямой и плоскостью.

Озвученное определение расстояния между параллельными прямой и плоскостью тесно связано со следующей теоремой.

Если прямая a параллельна плоскости , то все точки прямой a равноудалены от плоскости .

Проведем через произвольную точку прямой a плоскость параллельно плоскости . Прямая a при таком построении плоскости лежит в этой плоскости (если бы это было не так, то прямая a пересекала бы плоскость , а, значит, пересекала бы и плоскость в силу параллельности плоскостей и ). В статье расстояние между параллельными плоскостями мы доказали теорему о том, что все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости. Следовательно, все точки прямой a , которая лежит в плоскости , параллельной плоскости , равноудалены от плоскости , что и требовалось доказать.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Нахождение расстояния между прямой и параллельной ей плоскостью – теория, примеры, решения.

Расстояние между параллельными прямой и плоскостью обычно находится с помощью методов, изученных на уроках геометрии в 10-11 классах, — с использованием теоремы Пифагора, признаков равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п.

Когда в трехмерном пространстве введена прямоугольная система координат и требуется вычислить расстояние между заданными параллельными прямой и плоскостью, то применяется метод координат. Сейчас мы его подробно разберем, после чего рассмотрим решения нескольких примеров.

Поставим перед собой следующую задачу.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней заданы параллельные прямая a и плоскость , и требуется найти расстояние между прямой a и плоскостью .

Решение этой задачи будем строить на основе определения расстояния между прямой и параллельной ей плоскостью.

Искомое расстояние между заданными параллельными прямой и плоскостью по определению равно расстоянию от точки М₁ , лежащей на прямой a , до плоскости . Если мы определим координаты некоторой точки М₁ , лежащей на прямой a , и получим нормальное уравнение плоскости в виде , то мы сможем вычислить искомое расстояние , применив формулу (эта формула была получена в разделе нахождение расстояния от точки до плоскости).

Итак, алгоритм, позволяющий найти расстояние между параллельными прямой a и плоскостью , таков:

• находим координаты некоторой точки М₁ , лежащей на заданной прямой a (это легко сделать, если знать основные виды уравнений прямой в пространстве);
• получаем нормальное уравнение заданной плоскости вида (для этого нужно знать основные виды уравнения плоскости и при необходимости уметь приводить уравнение плоскости к нормальному виду);
• вычисляем требуемое расстояние между прямой a и параллельной ей плоскостью по формуле .

Воспользуемся полученным алгоритмом при решении задач, в которых требуется вычислить расстояние между параллельными прямой и плоскостью.

Найдите расстояние между параллельными прямой и плоскостью .

Очевидно, точка лежит на прямой, которую определяют канонические уравнения прямой в пространстве .

Получим нормальное уравнение плоскости . Для этого приведем заданное общее уравнение плоскости к нормальному виду: вычисляем нормирующий множитель , умножаем на него обе части заданного общего уравнения плоскости .

Осталось вычислить требуемое расстояние между заданными параллельными прямой и плоскостью как расстояние от точки до плоскости :

Найдите расстояние между прямой и параллельной ей плоскостью .

В рассматриваемой задаче прямая задана уравнениями двух пересекающихся плоскостей. Найдем координаты некоторой точки М₁ , лежащей на этой прямой. Координаты точки М₁ должны удовлетворять уравнениям прямой, то есть, — частное решение системы линейных уравнений . Найдем частное решение этой системы (при необходимости смотрите статью решение систем линейных уравнений). Приняв , приходим к системе уравнений , откуда находим . То есть, имеем .

Теперь получим нормальное уравнение плоскости, которую задает уравнение плоскости в отрезках вида . Для этого переходим к общему уравнению плоскости . Полученное общее уравнение плоскости уже является нормальным уравнением плоскости и его не нужно приводить к нормальному виду.

Осталось вычислить расстояние от точки до плоскости , которое равно искомому расстоянию между параллельными прямой и плоскостью: .

Видео:Параллельность прямой к плоскостиСкачать

Расстояние между прямой и параллельной ей плоскостью: определение и примеры нахождения

В статье ниже мы найдем определение, что же представляет собой расстояние между прямой и плоскостью, параллельными друг другу; разберем способ определить это расстояние и применим полученный навык в решении конкретных задач.

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Расстояние между прямой и параллельной ей плоскостью: определение

Расстояние между прямой и параллельной ей плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.

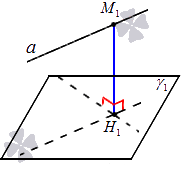
Пусть нам даны прямая a и плоскость ϒ 1 , ей параллельная. Используем некоторую точку М 1 , принадлежащую прямой a : проведем перпендикуляр из этой точки на заданную плоскость. Основание перпендикуляра на плоскости обозначим как Н 1 . Длина перпендикуляра М 1 Н 1 и будет являться расстоянием между исходными параллельными прямой и плоскостью.

Указанное определение имеет тесную взаимосвязь со следующей теоремой.

Когда прямая a параллельна плоскости ϒ 1 , все точки прямой a находятся на одинаковом расстоянии от плоскости ϒ 1 .

Используем любую произвольную точку на прямой a – проведем через нее плоскость ϒ 2 , параллельную заданной плоскости ϒ 1 . В таком построении прямая а принадлежит плоскости ϒ 2 (в ином случае прямая а пересекала бы эту плоскость, а, следовательно, пересекала бы и плоскость ϒ 1 , что противоречит исходному условию). В статье, которая разбирает тему расстояния между параллельными плоскостями, мы доказали теорему о том, что все точки одной из параллельных плоскостей равноудалены от точек другой плоскости. Таким образом, все точки прямой a , принадлежащей плоскости ϒ 2 (в свою очередь, параллельной плоскости ϒ 1 ) находятся на одинаковом расстоянии от плоскости ϒ 1 . Что и требовалось доказать.

Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Нахождение расстояния между параллельными прямой и плоскостью

Искомое расстояние между параллельными прямой и плоскостью обычно находится с использованием теоремы Пифагора, признаков равенства или подобия треугольников и пр.

Если же в трехмерном пространстве задана прямоугольная система координат, мы можем применить метод координат. Разберем его подробнее.

Допустим, в трехмерном пространстве зафиксирована некоторая прямоугольная система координат O x y z , в которой заданы прямая a и плоскость ϒ 1 , параллельные между собой. Требуется определить расстояние между заданными прямой и плоскостью.

Построим решение этой задачи на указанном выше определении расстояния между прямой и параллельной ей плоскостью.

Используем некоторую точку М 1 , принадлежащую прямой a : расстояние от этой точки до заданной плоскости и будет являться искомым расстоянием между параллельными прямой и плоскостью. Определим координаты точки М 1 как ( x 1 , y 1 , z 1 ) и запишем нормальное уравнение плоскости ϒ 1 : cos α · x + cos β · y + cos γ · z — p = 0 . Теперь мы можем вычислить искомое расстояние, для чего применим формулу:

M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p

Вывод этой формулы можно изучить в статье о нахождении расстояния от точки до плоскости.

Таким образом, мы можем сформулировать алгоритм для нахождения расстояния между прямой и параллельной ей плоскостью:

— определяем координаты точки, принадлежащей заданной прямой (для этого пригодятся навыки работы с основными видами уравнений в пространстве);

— записываем нормальное уравнение заданной плоскости вида cos α · x + cos β · y + cos γ · z — p = 0 (чтобы легко справиться с этим пунктом, следует повторить материал по основным видам уравнений плоскости и вспомнить навык приведения уравнения плоскости к нормальному виду);

— вычисляем искомое расстояние по формуле: M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p

Задана прямая x — 1 2 = y 0 = z + 1 1 и параллельная ей плоскость 3 x + 2 y — 6 z — 2 = 0 . Необходимо определить расстояние между ними.

Решение

Заданные условием задачи канонические уравнения прямой x — 1 2 = y 0 = z + 1 1 дают возможность определить точку М 1 ( 1 , 0 , — 1 ) , принадлежащую этой прямой.

Запишем нормальное уравнение исходной плоскости, т.е. преобразуем заданное условием задачи общее уравнение в нормальный вид. Вычислим нормирующий множитель: 1 3 2 + 2 2 + ( — 6 ) 2 = 1 7 и умножим на него обе части исходного общего уравнения плоскости:

3 x + 2 y — 6 z — 2 = 0 ⇔ 1 7 · 3 x + 2 y — 6 z — 2 = 1 7 · 0 ⇔ 3 7 x + 2 7 y — 6 7 z — 2 7

Теперь можем вычислить требуемое расстояние как расстояние от точки М 1 до плоскости 3 7 x + 2 7 y — 6 7 z — 2 7 = 0 :

M 1 H 1 = 3 7 · 1 + 2 7 · 0 — 6 7 · — 1 — 2 7 = 1

Ответ: 1 .

Заданы прямая 2 x — y + 9 = 0 2 x + y — 2 z + 3 = 0 и параллельная ей плоскость x — 3 2 + y 3 2 + z — 3 = 1 . Необходимо найти расстояние между ними.

Решение

Условием задачи прямая описывается уравнениями двух пересекающихся плоскостей. Определим координаты ( x 1 , y 1 , z 1 ) некой точки М 1 , принадлежащей этой прямой. Искомые координаты должны отвечать условиям уравнений прямой, т.е. координаты ( x 1 , y 1 , z 1 ) будут частным решением системы линейных уравнений 2 x — y + 9 = 0 2 x + y — 2 z + 3 = 0 . Найдем частное решение этой системы.

Примем z = 0 , тогда получим: 2 x — y = — 9 2 x + y = — 3 , откуда x = — 3 , y = 3 .

Таким образом, координаты точки М 1 равны ( — 3 , 3 , 0 ) .

Теперь запишем нормальное уравнение плоскости, заданной условием задачи уравнением плоскости в отрезках. Сначала осуществим переход к общему уравнению плоскости:

x — 3 2 + y 3 2 + z — 2 = 1 ⇔ — 2 3 x + 2 3 y — 1 3 z — 1 = 0

Полученное общее уравнение уже является нормальным уравнением плоскости, поэтому в дальнейших преобразованиях необходимости нет.

Наконец, вычислим расстояние от точки до плоскости, которое и будет являться требуемым расстоянием от заданной прямой к заданной плоскости:

M 1 H 1 = — 2 3 · — 3 + 2 3 · 3 — 1 3 · 0 — 1 = 0 = 3

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Расстояние от прямой до плоскости если прямая параллельна плоскости то

Раздел ІІ. СТЕРЕОМЕТРИЯ

§11. РАССТОЯНИЯ В ПРОСТРАНСТВЕ.

3. Расстояние от прямой до плоскости.

Если прямая принадлежит плоскости или пересекает плоскость, то естественно считать, что расстояние от прямой до плоскости равна нулю.

Расстоянием от прямой до параллельной ей плоскости называют длину перпендикуляра, проведенного из любой точки прямой к плоскости.

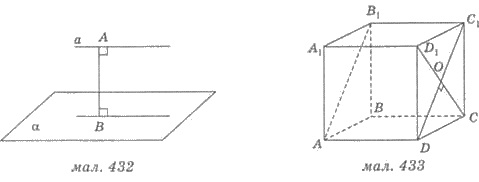
На рисунке 432: а || α , А 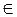а, АВ α . Длина отрезка АВ — расстояние от прямой а в плоскости α .

Пример. АВС D А ₁ В ₁ С ₁ D ₁ — куб (рис. 433), ребро которого равно 2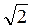 см.

Найти расстояние от прямой ВС до плоскости АВ₁С₁.

Решения. 1) Так как ВС || В ₁ С ₁ , то прямая ВС параллельна плоскости АВ₁С₁.

2) С D ₁ С ₁ D , точка О — точка пересечения диагоналей боковой грани С D ₁ и С ₁ D .

3) СО АВ₁С₁; СО — искомое расстояние.

📺 Видео

7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Расстояние от точки до плоскости / Вывод формулыСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

ЕГЭ математикa задание C2 Расстояние точка плоскость 5Скачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

✓ Расстояние до плоскости | ЕГЭ-2016. Задание 13. Математика. Профильный уровень | Борис ТрушинСкачать

Урок 10. Расстояние от точки до плоскости. Компенсация расстояний. Стереометрия с нуля.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Урок 11. Задачи из ЕГЭ. Расстояние от точки до прямой и плоскости. Стереометрия с нуля.Скачать

РАССТОЯНИЕ от ТОЧКИ до ПЛОСКОСТИ 10 класс стереометрияСкачать

Расстояние между скрещивающимися прямыми за 1 минуту. #математикапрофиль2023 #егэ2023 #школа #fypСкачать