Основание пирамиды треугольник с углами

Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать

Ваш ответ

Видео:Трехгранный угол в пирамидеСкачать

Похожие вопросы

• Все категории
• экономические 43,288
• гуманитарные 33,620
• юридические 17,900
• школьный раздел 607,127
• разное 16,830

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

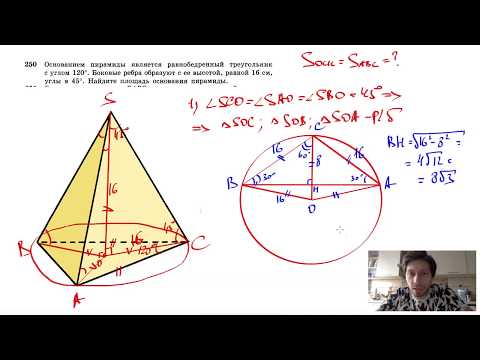
Видео:№250. Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребраСкачать

Основание пирамиды — прямоугольный треугольник с острым углом альфа?

Геометрия | 10 — 11 классы

Основание пирамиды — прямоугольный треугольник с острым углом альфа.

Расстояние от основания высоты пирамиды до вершины этого угла равно в.

Все двугранные углы при основании пирамиды равны бета.

Найти объём пирамиды.

Помогите найти площадь основания побыстрей пожалуста!

Второй угол треугольника в основании (90 — альфа).

Теперь главное — ясно, что вершина пирамиды проецируется в центр вписаной окружности.

Это потому, что основание высоты равноудалено от сторон на расстояния, равные высоте пирамиды, умноженной на ctg(бета).

Если аккуратно построить двугранные углы боковых граней, опуская перпендикуляры на стороны основания, то это сразу видно.

Центр вписаной окружности лежит на пересечении биссектрис.

r = b * sin(альфа / 2) ;

Боковые стороны тоже легко вычисляются, один катет = r + b * cos(альфа / 2) ;

второй = r + r * ctg(45 — альфа / 2).

Высота пирамиды равна r * tg(бета).

Отсюда всё находится.

S = (1 / 2) * (b ^ 2) * (sin(альфа / 2) + cos(альфа / 2)) * sin(альфа / 2) * (1 + ctg(45 — альфа / 2)) ;

Наверно, это выражение можно упростить.

Мне удалось до такого выражения :

S = (b ^ 2 / 2) * (1 + sin(альфа) — cos(альфа)) * (1 + sin(альфа) + cos(альфа)) / (2 * cos(альфа))

Надеюсь, я нигде не ошибся.

На всякий добавил скан, как я упрощал.

V = (1 / 3) * S * b * sin(альфа / 2) * tg(бета).

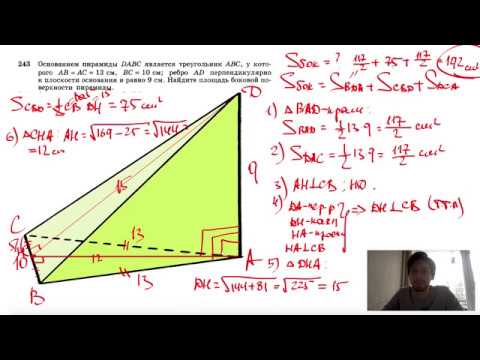
Видео:№243. Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС= 13 см, ВС=10 см; реброСкачать

Все двугранные углы при основании пирамиды равны 60 градусов?

Все двугранные углы при основании пирамиды равны 60 градусов.

Найдите площадь основания пирамиды, если Боковая поверхность ее равна 36.

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Основание пирамиды ромб со стороной 12 м и острым углом 60 градусов ?

Основание пирамиды ромб со стороной 12 м и острым углом 60 градусов .

Двугранный углы при основании пирамиды равны 45 градусов .

Вычислите длину высоты пирамиды.

Видео:Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Основанием пирамиды служит ромб с острым углом, равным 60?

Основанием пирамиды служит ромб с острым углом, равным 60.

Сторона ромба и высота пирамиды равны а, основание высоты пирамиды совпадает с вершиной острого угла ромба.

Найдите площадь боковой поверхности пирамиды.

Видео:Площади треугольников с равным углом.Скачать

Основание пирамиды — правильный треугольник?

Основание пирамиды — правильный треугольник.

Две боковые грани пирамиды перпендикулярны плоскости основания, а третья — наклонена к ней под углом альфа.

Высота пирамиды равна H.

Найти полную поверхность пирамиды.

Нужно подробное решение.

Видео:№251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать

Сторона основания правильной четырехугольной пирамиды равна а?

Сторона основания правильной четырехугольной пирамиды равна а.

Двугранные углы при основании равны а (альфа).

Определите площадь полной поверхности пирамиды.

Видео:Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основанияСкачать

Основание пирамиды — равнобедренный треугольник с боковой стороной b и углом при основании бета?

Основание пирамиды — равнобедренный треугольник с боковой стороной b и углом при основании бета.

Все двугранные углы при основании пирамиды равны альфа.

Найдите обьем пирамиды.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Основание пирамиды ромб со стороной 10 см?

Основание пирамиды ромб со стороной 10 см.

Высота пирамиды — 6 см.

Найти объем пирамиды , если все двугранные углы при ее основании равны 45 градусов.

Видео:⚡ Прямой эфир | Искусственные пещеры Барабар - создание высшего разума. Уникальные данныеСкачать

Помогите, пожалуйста, хотя бы с одной задачей : * * 1?

Помогите, пожалуйста, хотя бы с одной задачей : * * 1.

Основание пирамиды – треугольник со сторонами 13, 14 и 15 см.

Все двугранные углы при основании пирамиды равны 45º.

Найдите объем пирамиды.

2. Основание пирамиды – равнобедренный треугольник с углом при вершине α и радиусом описанной окружности R.

Все боковые грани пирамиды образуют с ее высотой углы равные β.

Найдите объем пирамиды.

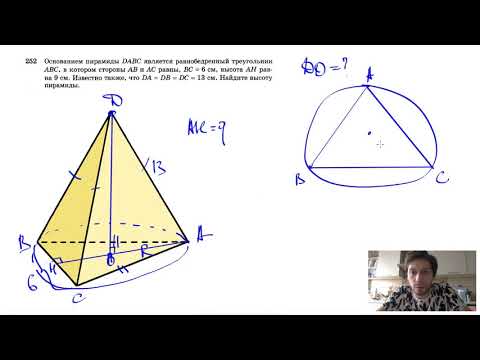
Видео:№252. Основанием пирамиды DABC является равнобедренный треугольник ABC, в котором АВ = АС, ВС=6 смСкачать

Основание пирамиды ромб с углом 30 градусов, все двугранные углы при рёбрах основания равны 60 градусов?

Основание пирамиды ромб с углом 30 градусов, все двугранные углы при рёбрах основания равны 60 градусов.

Найти объём пирамиды, если её высота равна 3 корня квадратных из 3.

Видео:№245. Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. ПлоскостиСкачать

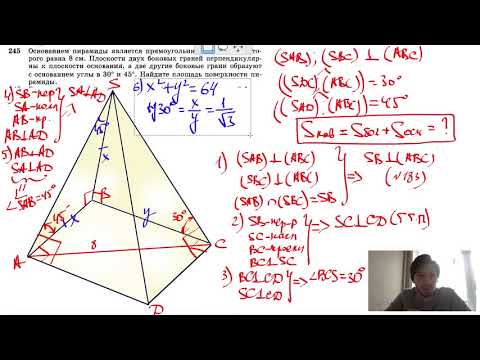
В правильной треугольной пирамиде высота основания равна h, боковые ребра наклонены к основанию под углом альфа?

В правильной треугольной пирамиде высота основания равна h, боковые ребра наклонены к основанию под углом альфа.

Найти объем пирамиды.

На этой странице сайта размещен вопрос Основание пирамиды — прямоугольный треугольник с острым углом альфа? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

100, т. К накрест лежащий углу 80 градусов равен 80 , а Х смежный с ним , те 100.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Решение задач с использованием свойств различных видов пирамид

Разделы: Математика

Изучение пирамиды и ее элементов представляет широкие возможности для составления и решения задач на различных видах пирамид по следующим темам:

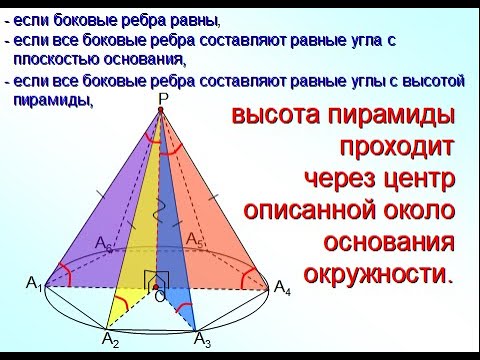
• Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.
• Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания.
• Пирамиды, в которых заданы расстояния между точками и элементами пирамиды.

Действующие учебники геометрии либо не содержат , либо содержат в недостаточном количестве задачи по этим темам.

Как показала практика, учащиеся с большим интересом принимают участие не только в решении данных задач, но и в их составлении. Они с удовольствием предлагают различные решения придуманных ими задач.

К этому учащихся необходимо подводить хорошо продуманной системой теоретических положений и практических упражнений.

Учебники Л.С. Атанасяна и др. “Геометрия 10–11” и А.В.Погорелова “Геометрия 10–11” содержат опорный теоретический материал по теме “Пирамида и ее элементы”.

В дополнение к нему можно рассмотреть следующие свойства часто встречающихся видов пирамид.

Теория.

Теоремы о пирамидах, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.

• Если все боковые ребра пирамиды составляют с плоскостью основания равные углы, то:

а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды;

б) все боковые ребра пирамиды равны между собой.

• Если основание высоты пирамиды совпадает с центром окружности, описанной около ее основания, то:

а) все боковые ребра пирамиды образуют с плоскостью основания равные углы;

в) все боковые ребра пирамиды равны между собой.

• Если все боковые ребра пирамиды равны, то:

а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды;

б) все боковые ребра пирамиды составляют с плоскостью ее основания равные между собой углы.

• Если высота пирамиды пересекает ее основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в ее основание.
• Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.
• Если у треугольной пирамиды все боковые ребра равны, а в основании лежит прямоугольный треугольник, то грань, содержащая его гипотенузу, перпендикулярна основанию. Основание высоты данной пирамиды является середина гипотенузы.

Теоремы о пирамидах, в которых одна или две боковые грани перпендикулярны плоскости основания.

• Если пирамида содержит ровно одну боковую грань, которая перпендикулярна плоскости основания, то высота такой пирамиды лежит в этой боковой грани.
• Если пирамида содержит две смежные боковые грани, перпендикулярные плоскости основания, то высотой такой пирамиды является боковое ребро, общее для этих граней.
• Если в пирамиде две не смежные боковые грани перпендикулярны плоскости основания, то высота такой пирамиды лежит на прямой пересечения плоскостей этих граней.
• Если боковое ребро пирамиды перпендикулярно основанию, то и боковые грани, содержащие это ребро, перпендикулярны основанию.
• Если в четырехугольной пирамиде в основании ромб, и две смежные боковые грани перпендикулярны основанию, то боковые грани данной пирамиды – две пары равных треугольников.

Задачи для решения.

Задания из книги “Самостоятельные и контрольные работы по геометрии для 11-го класса” Ершовой А.П., Голобородько В.В.

Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.

Вариант А.

1. Основание пирамиды SABCD – прямоугольник АВСД со сторонами 6 и 8 см. Все боковые ребра пирамиды равны 13 см.

а) Опишите построение высоты пирамиды SO.

б) Докажите равенство отрезков АО, ВО, СО и ДО.

в) Обоснуйте положение точки О в прямоугольнике АВСД и найдите длину высоты SO.

1. Основание пирамиды – равнобедренный треугольник с основанием а и углом при вершине . Все двугранные углы при основании пирамиды равны .

а) Опишите построение высоты пирамиды, высот боковых граней и их проекций на плоскость основания. Обоснуйте двугранные углы при основании пирамиды.

б) обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике.

в) Найдите высоту пирамиды.

Вариант Б.

1. Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при основании . Все боковые ребра пирамиды наклонены к плоскости основания под углом .

а) Обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике.

б) Определите, при каких значениях ? высота пирамиды будет находиться вне пирамиды.

в) Найдите высоту пирамиды.

1. Основание пирамиды – ромб с большей диагональю d и острым углом . Все двугранные углы при основании пирамиды равны .

а) Обоснуйте данные двугранные углы и положение основания высоты пирамиды в ромбе.

б) Найдите высоту пирамиды.

в) Двумя способами – путем вычисления площадей боковых граней и с помощью теоремы об ортогональной проекции многоугольника – найдите боковую поверхность пирамиды. Сравните полученные результаты.

Вариант В.

1. Основание пирамиды – треугольник с углами и . Точка высоты пирамиды, удаленная от плоскости основания на расстояние d, равноудалена от концов бокового ребра. Все боковые ребра пирамиды наклонены к плоскости основания под углом .

а) Обоснуйте положение основания высоты пирамиды.

б) При каких условиях высота пирамиды лежит внутри пирамиды?

в) Найдите высоту пирамиды.

г) Найдите площадь основания пирамиды.

1. В основании пирамиды лежит равнобокая трапеция с острым углом . Высота пирамиды равна Н, а все двугранные углы при основании равны .

а) обоснуйте положение основания высоты пирамиды.

б) Найдите высоту трапеции, лежащей в основании пирамиды.

в) Не вычисляя площадей боковых граней, найдите боковую поверхность пирамиды.

Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания.

Вариант А.

1. Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при вершине . Боковые грани пирамиды, содержащие стороны данного угла перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом .

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте угол .

в) Найдите площадь третьей боковой грани.

г) Найдите боковую поверхность пирамиды.

1. Основание пирамиды – правильный треугольник со стороной а. Одна из боковых граней пирамиды перпендикулярна плоскости основания, а две другие – наклонены к ней под углом .

а) Из вершины пирамиды в плоскости грани, перпендикулярной основанию, проведите перпендикуляр к ребру основания и обоснуйте, почему он будет высотой пирамиды.

б) Обоснуйте углы наклона, равные .

в) Докажите, что основание высоты пирамиды равноудалено от двух сторон правильного треугольника, и обоснуйте положение основания высоты на стороне правильного треугольника.

г) Найдите боковую поверхность пирамиды.

Вариант Б.

1. Основание пирамиды – квадрат со стороной а, две смежные боковые грани пирамиды перпендикулярны плоскости основания, а две другие – наклонены к ней под углом .

а ) Обоснуйте положение высоты пирамиды.

б ) Обоснуйте углы, равные .

в ) Докажите, что боковые грани пирамиды попарно равны.

г ) Найдите боковую поверхность пирамиды.

1. Основание пирамиды – прямоугольный треугольник с гипотенузой с и острым углом . Боковая грань, содержащая катет, противолежащий данному углу , перпендикулярна плоскости основания, а две другие грани наклонены к ней под углом .

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты пирамиды.

в) Найдите высоту пирамиды.

г) Найдите боковую поверхность пирамиды.

Вариант В.

1. Основание пирамиды – ромб с тупым углом . Две боковые грани, содержащие стороны этого угла, перпендикулярны плоскости основания, а две другие – наклонены к ней под углом . Высота пирамиды равна Н.

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте углы, равные .

в) Найдите боковую поверхность пирамиды.

1. Основание пирамиды – прямоугольная трапеция с острым углом ? и прилежащей к нему боковой стороной . Боковая грань, содержащая большее основание трапеции, перпендикулярна плоскости основания, а три другие грани наклонены к ней под углом .

а ) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты пирамиды.

в) Найдите площадь основания пирамиды.

г) Найдите боковую поверхность пирамиды.

Пирамиды, в которых заданы расстояния между точками и элементами пирамиды.

Вариант А.

1. В правильной треугольной пирамиде боковое ребро наклонено к плоскости основания под углом . Расстояние от середины высоты пирамиды до середины бокового ребра равно d.

б ) Найдите площадь основания пирамиды.

1. В правильной четырехугольной пирамиде двугранный угол при основании равен . Расстояние от середины высоты пирамиды до ее апофемы равно l . Найдите боковую поверхность пирамиды.

Вариант Б.

1. В правильной четырехугольной пирамиде двугранный угол при основании равен . Расстояние от основания высоты пирамиды до середины апофемы равно l . Найдите полную поверхность пирамиды.
2. Основание пирамиды – равнобедренный треугольник с углом при вершине. Все боковые ребра пирамиды наклонены к плоскости основания под углом . Биссектриса этого угла пересекает высоту пирамиды в точке, удаленной от бокового ребра на расстояние d.

б ) Найдите площадь основания пирамиды.

Вариант В.

1. Основание пирамиды – равнобедренный треугольник с углом при основании . Все двугранные углы при основании пирамиды равны . Отрезок, соединяющий точки пересечения медиан боковых граней, содержащих боковые стороны треугольника, равен m. Найдите боковую поверхность пирамиды.
2. Основание пирамиды – прямоугольный треугольник с острым углом . Боковые грани пирамиды, содержащие катеты треугольника, перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом . Расстояние от основания высоты пирамиды до этой грани равно l. Найдите боковую поверхность пирамиды.

Указанный в статье перечень задач может быть расширен Вами и вашими учениками.

📹 Видео

Комплексный чертеж усеченной 5-гранной пирамидыСкачать

Загадки Пирамид с точки зрения науки Документальный фильм 2021 National Geographic FULL HDСкачать

№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Делаем модель пирамиды для решения задачи по стереометрииСкачать

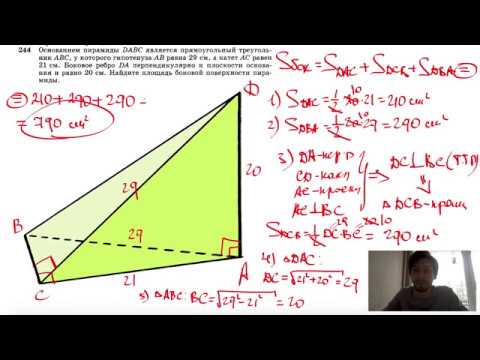
№244. Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенузаСкачать

№247. Двугранные углы при основании пирамиды равны. Докажите, что: а) высота пирамидыСкачать