К двум окружностям с центрами O1 и O2 и радиусами 6 и 3 проведены три общие касательные: одна внутренняя и две внешних. Пусть A и B — точки пересечения общей внутренней касательной с общими внешними.
а) Докажите, что около четырехугольника O1AO2B можно описать окружность.
б) Найдите расстояние между точками касания окружностей с их общей внутренней касательной, если известно, что O1O2 = 15.
а) Пусть: F и E — общие точки окружности с центром O2 и общих внешних касательных, G и H — общие точки другой заданной окружности и тех же внешних касательных, N и Q — общие точки заданных окружностей и общей внутренней касательной; T — точка пересечения O1O2 и AB.
AO1 есть биссектриса угла HAB, AO2 — биссектриса угла EAB. А эти углы являются смежными. Так как биссектрисы двух смежных углов взаимно перпендикулярны, то ∠O1AO2 = 90°. Аналогично докажем, что ∠O1BO2 = 90°. Таким образом, получаем , что сумма одной пары противоположных углов четырехугольника O1AO2B равна 180°. Коли это так, то сумма и другой пары противоположных углов того же четырехугольника обязана быть равной 360° − 180° = 180°. То есть выполняется признак вписанного четырехугольника, что и требовалось доказать.
б) Заметим, что O1Q || O2N как два перпендикуляра к одной и той же прямой AB.
Δ O2NT,
Пусть тогда
В
В
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Содержание
Видео:Геометрия Окружности с центрами в точках O1 и O2 не имеют общих точек. Внутренняя общая касательнаяСкачать 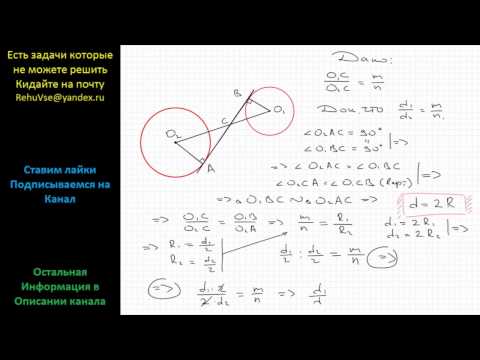 Две окружности разного радиуса с центрами в точках О1 и О2 пересекаются в точках А и В. Докажите, что линия центров О1О2 перпендикулярна общей хорде АВ этих окружностей.Видео:Геометрия Две окружности радиуса R с центрами O1 и O2 касаются друг друга. Их пересекает прямаяСкачать  Ваш ответВидео:Построение внешней касательной к двум дугам окружностей. Урок11.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  решение вопросаВидео:Геометрия В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимноСкачать  Похожие вопросы
Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. Видео:Построение общей внешней касательной к двум окружностямСкачать  Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д?Геометрия | 5 — 9 классы Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д. Используя переллельный перенос докажите , что четырехугольник О1МДО2 является параллелограммом. О1М и О2Д — радиусы равных окружностей. Следовательно, они равны. Опустив перпендикуляры Ма из М и Дн из Д на прямую О1О2, получим равные между собой отрезки, ониравные также высоте четырехугольника О1О2ДМ. Прямоугольные треугольники О1аМ и О2нД равны по гипотенузе и катету, и их основания лежат на одной прямой. Сдвигая окружность О1 по прямой О1О2, получим совмещениеО1 и О2, т. Совпадут и перпендикулярные отрезки между прямыми, опущенные из точек пересечения радиусов с окружностью. Расстояние между их вершинами М и Д, О1 и О2 равны. Следовательно, МД = О1О2. Четырехугольник, в котором стороны попарно равны и параллельны, — параллелограмм Четырехугольник О1МДО2 является параллелограммом, что и требовалось доказать. Видео:Касательные к окружностиСкачать  Докажите что если две окружности с центрами О и О1 пересекаются в точках А и В, то АВ _|_ ОО1?Докажите что если две окружности с центрами О и О1 пересекаются в точках А и В, то АВ _|_ ОО1. Видео:Внешняя касательная к двум окружностямСкачать  Диагонали ромба «abcd» пересекаются в точке «о» ?Диагонали ромба «abcd» пересекаются в точке «о» . Докажите , что прямая «bd» касается окружности с центром «а» и радиусом , равным «ос». Видео:Г: Три равные окружности с центрами О1, О2, О3 и радиусом R попарно касаются друг друга в точках А ВСкачать  Диагонали ромба АВСD пересекаются в точке О?Диагонали ромба АВСD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС. Видео:Планиметрия | конкретные задачи | касательные и окружности | 1Скачать  Две окружности с равными радиусами пересекаются в двух точках?Две окружности с равными радиусами пересекаются в двух точках. Докажите, что их общая хорда перпендикулярна к отрезку, соединяющему центры окружностей. Видео:Касательные к двум окружностям.Скачать  Докажите, что прямая, проходящая через центр окружности, пересекает окружность в двух точках?Докажите, что прямая, проходящая через центр окружности, пересекает окружность в двух точках. Видео:№675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке АСкачать  Две окружности равных радиусов пересекаются в точках А и В?Две окружности равных радиусов пересекаются в точках А и В. Докажите, что отрезок, соединяющий центры окружностей, перпендикулярен АВ. Видео:Построение общей касательной к двум окружностямСкачать  Через точку А к окружности проведены касательная АБ и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности?Через точку А к окружности проведены касательная АБ и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности. Найдите радиус окружности если AB = 12, а AF = 18. Видео:К двум окружностям проведены общие касательныеСкачать  Окружности радиусов 4 и 3, расстояние между центрами которых равно 5, пересекаются в точках А и В?Окружности радиусов 4 и 3, расстояние между центрами которых равно 5, пересекаются в точках А и В. Через точку В проведена прямая, пересекающая большую окружность в точке С, а меньшую в точке D ( точка В лежит между С и D). Опредилите косинусы углов треугольника АСD. Видео:Касательная к двум окружностям разного диаметра.2 часть.Скачать  Через концы диаметра AB окружности с центром О, проведены параллельные прямые, пересекающие окружность в точках М и К?Через концы диаметра AB окружности с центром О, проведены параллельные прямые, пересекающие окружность в точках М и К. Докажите, что МК — диаметр окружности. С рисунком, пожалуйста! Видео:Внутренняя касательная к двум окружностямСкачать  Две окружности пересекаются в точках P и Q?Две окружности пересекаются в точках P и Q. Через точку A первой окружности проведены прямые AP и AQ, пересекающие вторую окружность в точках B и C. Докажите, что касательная в точке A к первой окружности параллельна прямой BC. На странице вопроса Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи. 📽️ Видео7.43.1. Планиметрия. Гордин Р.К.Скачать  Касательная к двум окружностям разного диаметра.Скачать  Построение общей внутренней касательной к двум окружностямСкачать  Касательная к двум окружностям разного диаметра.3 часть.Скачать  10.19.1. Планиметрия. Гордин Р.К.Скачать  |





