Авторы: Мерзляк А.Г. , Полонский В.Б. , Рабинович Е.М. , Якир М.С. .
Издательства: Просвещение, Вентана-граф 2017-2021
Тип: Дидактические материалы, Алгоритм успеха
Подробный решебник (ГДЗ) по Геометрии за 9 (девятый) класс дидактические материалы — готовый ответ вариант 1 — 174. Авторы учебника: Мерзляк, Полонский, Рабинович, Якир. Издательство: Вентана-граф 2017-2021.
- Похожие ГДЗ
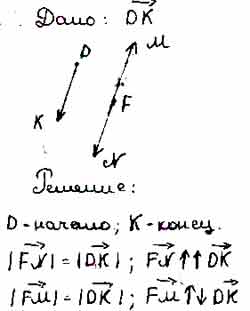
- На рисунке 36 изображён вектор DK. Укажите начало и конец этого вектора. Отложите от точки F вектор, равный вектору DK, и вектор,
- Вопрос вызвавший трудности
- Ответ подготовленный экспертами Учись.Ru
- Геометрия
- Понятие вектора в пространстве
- Операции над векторами
- Компланарные векторы
- Разложение вектора на некомпланарные вектора
- 📸 Видео
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Похожие ГДЗ
ГДЗ учебник геометрия 9 класс А.Г. Мерзляк
ГДЗ Самостоятельные и контрольные работы геометрия 9 класс Мерзляк А.Г. углубленный уровень
ГДЗ учебник геометрия 9 класс Мерзляк А.Г. углубленный уровень
ГДЗ Математические диктанты, Контрольные работы (Методическое пособие) геометрия 9 класс Буцко Е.В.
ГДЗ Рабочая тетрадь геометрия 9 класс Мерзляк А.Г.
174. На рисунке 9 изображён вектор АС. Укажите начало и конец этого вектора. Отложите от точки М вектор, равный вектору АС, и вектор, противоположно направленный вектору АС, модуль которого равен модулю вектора АС.
Видео:Координаты вектора. 9 класс.Скачать

На рисунке 36 изображён вектор DK. Укажите начало и конец этого вектора. Отложите от точки F вектор, равный вектору DK, и вектор,
В 17:08 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Вопрос вызвавший трудности
Видео:Сложение векторов. 9 класс.Скачать

Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: На рисунке 36 изображён вектор DK. Укажите начало и конец этого вектора. Отложите от точки F вектор, равный вектору DK, и вектор, противоположно направленный вектору DK, модуль которого равен модулю вектора DK.
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Волкова Сима Кимовна — автор студенческих работ, заработанная сумма за прошлый месяц 77 800 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.
Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.
Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
Видео:Координаты точки и координаты вектора 1.Скачать

Геометрия
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Понятие вектора в пространстве
Напомним, что в курсе планиметрии мы уже подробно изучали вектора и действия с ними. При этом предполагалось, что все вектора располагаются в одной плоскости. Однако можно расширить понятие вектора так, чтобы они использовались и в стереометрии. В таком случае вектора уже могут располагаться в различных плоскостях.
Начнем с определения вектора:
Конец вектора обозначают с помощью стрелки. Посмотрим на рисунок:
Здесь показаны сразу три вектора:
У вектора АВ начало находится в точке А, а конец – в точке В. Аналогично у вектора С D точка С – это начало, а D – это конец. В обоих случаях начало и конец – это различные точки, поэтому АВ и CD именуют ненулевыми векторами. Если же начало и конец находятся в одной точке, например в Т, то получается нулевой вектор ТТ. Всякую точку в пространстве можно рассматривать как нулевой вектор:
Длина вектора АВ – это длина соответствующего ему отрезка АВ. Для обозначения длины используют квадратные скобки:
Естественно, что нулевой вектор имеет нулевую длину.
Далее напомним понятие коллинеарных векторов:
Коллинеарные вектора могут быть либо сонаправленными, либо противоположно направленными. Сонаправленные вектора находятся на сонаправленных лучах. Рассмотрим пример с кубом:
Здесь показаны вектора AD и ВС. Они сонаправленные, этот факт записывается так:
Вектора AD и FE располагаются на скрещивающихся прямых, поэтому они не коллинеарны. Их нельзя считать ни сонаправленными, ни противоположно направленными.
Сонаправленные вектора, имеющие одинаковую длину, именуются равными.
Рассмотрим несколько простейших задач.
Задание. В прямоугольном параллелепипеде АВС DA 1 B 1 C 1 D 1 известны три его измерения:
Решение. Для нахождения длин этих векторов достаточно вычислить длину отрезков СВ, DB и DB 1. Проще всего вычислить СВ, ведь отрезки СВ и AD одинаковы как стороны прямоугольника АВ CD :
Задание. На рисунке показан правильный тетраэдр АВС D . Точки M , N , P и Q являются серединами тех сторон, на которых они располагаются. Какие вектора из отмеченных на рисунке равны между собой?
Решение. Легко заметить, что вектора DP и PC находятся на одной прямой DC и сонаправлены, при этом их длина одинакова, ведь Р – середина DC . Тогда эти вектора по определению равны:
Вектора АМ и МВ также коллинеарны и имеют одинаковую длину, но они противоположно направлены, а потому равными не являются.
Теперь заметим, что отрезки MN , MQ , PQ и NP – это средние линии в ∆ ABD , ∆ АВС, ∆ BCD и ∆ ACD соответственно. По свойству средней линии получаем, что MN || BD , PQ || BD , MQ ||АС и NP ||АС. Отсюда по свойству транзитивности параллельности получаем, что MN || PQ и MQ || NP . Это значит, что четырехугольник MQPN – это параллелограмм, а у него противоположные стороны одинаковы:
Видео:Вычитание векторов. 9 класс.Скачать

Операции над векторами
Правила сложения векторов в стереометрии не отличаются от правил в планиметрии. Пусть надо сложить два вектора, а и b . Для этого отложим вектор а от какой-нибудь точки А, тогда его конец окажется в некоторой точке В. Далее от В отложим вектор b , его конец попадет в какую-то точку С. Тогда вектор АС как раз и будет суммой a и b :
Такой метод сложения векторов именуется правилом треугольника. Если нужно сложить больше двух векторов, то используют правило многоугольника. В этом случае необходимо каждый следующий вектор откладывать от конца предыдущего. При этом в стереометрии вектора могут располагаться в различных плоскостях, то есть они на самом деле многоугольник не образуют:
Напомним, что в планиметрии существовали так называемые противоположные вектора. Есть они и в стереометрии:
Главное свойство противоположных векторов заключается в том, что в сумме они дают нулевой вектор:
Заметим, что для получения противоположного вектора достаточно поменять его начало и конец, то есть в записи вектора обозначающие его буквы надо просто записать в обратном порядке:
C помощью противоположного вектора легко определить операцию вычитания векторов. Чтобы из вектора а вычесть вектор b , надо всего лишь прибавить к a вектор, противоположный b :
Далее рассмотрим умножение вектора на число. Пусть вектор а умножается на число k . В результате получается новый вектор b , причем
1) b и a будут коллинеарными векторами;
2) b будет в k раз длиннее, чем вектор a .
Если k – положительное число, то вектора a и b будут сонаправленными. Если же k a и b будут направлены противоположно.
Уточним, что если | k | b будет не длиннее, а короче вектора a . Наконец, если k = 0, то и b будет иметь нулевую длину, то есть b окажется нулевым вектором.
Задание. Дан параллелепипед АВС D А1В1С1 D 1. Постройте вектор, который будет являться суммой векторов:
Решение. В каждом случае необходимо заменить один из векторов в сумме на другой равный ему вектор так, чтобы можно было применить правило треугольника.
В задании а) вектор А1 D 1 заменить равным ему вектором ВС. В итоге получится вектор АС.
В задании б) заменяем А D 1 на вектор ВС1. Также можно было бы заменить АВ на D 1 C 1. В обоих случаях сумма окажется равной АС1.
В задании в) удобно DA заменить на C 1В1, тогда искомой суммой будет вектор С1В.
В задании г) производим замену DD 1 на равный ему вектор BB 1. Тогда сумма DB и BB 1– это вектор DB 1.
В задании д) необходимо заменить ВС на В1С1. В итоге получаем вектор DC :
Задание. В пространстве отмечены точки А, В, С и D . Выразите вектор АВ через вектора:
Решение. В случае а) сначала запишем очевидное равенство векторов, вытекающее из правило многоугольника:
Обратите внимание, что здесь у каждого следующего слагаемого начальная точка совпадает с конечной точкой предыдущего слагаемого, поэтому равенство и справедливо:
Однако по условию а) нам надо использовать другие вектора для выражения АВ. Мы можем просто заменить вектора CD и DB на противоположные:
Теперь можно составить и выражение для АВ:
Аналогично решаем и задания б) и в):
Задание. Р – вершина правильной шестиугольной пирамиды. Докажите, что сумма векторов, совпадающих с ребрами этой пирамиды и начинающихся в точке Р, в точности равна сумме векторов, которые совпадают с апофемами пирамиды и при этом также начинаются в точке Р.
Решение. Обозначим вершины буквами А1, А2, … А6, а середины сторон шестиугольника, лежащего в основании, буквами Н1, Н2, … Н6, как это показано на рисунке:
Нам надо показать, что сумма красных векторов равна сумме черных векторов:
Теперь отдельно построим правильный шестиугольник, лежащий, в основании пирамиды:
Ясно, что вектора, образованные сторонами этого шестиугольника, в сумме дают нулевой вектор (по правилу многоугольника):
Так как точки Н1, Н2, … Н6 – середины сторона, то вектора Н6А6, Н5А5,…Н1А1 будут вдвое короче векторов А1А6, А6А5, … А2А1. При этом они находятся на одних прямых, поэтому справедливы равенства:
Таким образом нам удалось из верного равенства (3) доказать (2), из которого в свою очередь следует справедливость и (1), ч. т. д.
Задание. Упростите выражения:
Решение. Здесь надо просто применить законы сложения и умножения векторов, как это делалось и в курсе планиметрии. Сначала раскрываем скобки, а потом приводим подобные слагаемые:
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Компланарные векторы
Если мы отложим несколько векторов от одной точки, то они либо будут находиться в одной плос-ти, либо располагаться в различных плос-тях. В первом случае их именуют компланарными векторами, а во втором – некомпланарными.
Любые два вектора будут компланарны, ведь при их откладывании от одной точки мы получаем две пересекающихся прямых, а через них всегда можно провести плос-ть. Однако если векторов более двух, то они могут быть как компланарны, так и некомпланарны.
Рассмотрим для примера параллелепипед:
Здесь вектора АС, АВ и АD компланарны, так как все они принадлежат одной грани (то есть плос-ти) АВСD. А вектора АВ, АD и АА1 некомпланарны, ведь через них нельзя провести одну плос-ть.
Очевидно, что если из трех векторов любые два коллинеарны, то вся тройка векторов компланарна, ведь при откладывании векторов от одной точки коллинеарные вектора окажутся на одной прямой.
Существует признак компланарности векторов:
Напомним, что подразумевается под разложением вектора. Пусть есть вектора а, b и c. Если существуют такие числах и y, при которых выполняется равенство
то говорят, что вектор с разложен по векторам а и b, причем числа xи y называются коэффициентами разложения.
Докажем сформулированный признак. Пусть есть три вектора а, b и c, а также числа xи y, такие, что
Эти вектора находятся в одной плос-ти ОАВ. Теперь от той же точки О отложим вектора ха и уb, концы которых окажутся в точках А1 и В1:
Естественно, что вектора ОА1 и ОВ1 также окажутся в плос-ти ОАВ. Тогда и их сумма будет принадлежать этой плос-ти, а эта сумма как раз и есть вектор с:
В итоге получили, что а, b и с располагаются в одной плос-ти, то есть они компланарны.
Справедливо и обратное утверждение. Если вектора а, b и с компланарны, но а и b неколлинеарны, то вектор с можно разложить на вектора a и b. Это утверждение прямо следует из изученной в 9 классе теоремы о разложении векторов. Важно отметить, что коэффициенты такого разложения определяются однозначно.
Для сложения тройки некомпланарных векторов можно применить так называемое правило параллелепипеда. Если есть три некомпланарных вектора, то можно отложить их от одной точки О и далее построить параллелепипед, в котором эти вектора будут ребрами. Тогда диагональ этого параллелепипеда, выходящая из точки О, и будет суммой этих трех векторов:
Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Разложение вектора на некомпланарные вектора
Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:
Для доказательства рассмотрим три некомпланарных вектора а, bи c, а также произвольный вектор р. Отложим их от одной точки О. Обозначим концы этих векторов большими буквами А, В, С и Р:
Через ОВ и ОА можно провести некоторую плос-ть α. Точка С ей принадлежать не может, ведь ОА, ОВ и ОС – некомпланарные вектора. Проведем через Р прямую, параллельную ОС. Так как ОС пересекает α, то и параллельная ей прямая также пересечет α в некоторой точке Р1. (Примечание. Если Р принадлежит α, то точки Р и Р1 совпадут, то есть вектор Р1Р будет нулевым).
Далее через точку Р1 в плос-ти α проведем прямую, параллельную ОВ, которая пересечет ОА в точке Р2. Заметим, что вектор ОР2 находится на той же прямой, что и вектор ОА, то есть они коллинеарны, поэтому существует такое число х, что
Итак, мы показали, что у произвольного вектора p есть разложение на заранее заданные некомпланарные вектора. Осталось показать, что существует только одно такое разложение. Докажем это методом от противного. Пусть есть второе разложение с другими коэффициентами х1, у1 и z1:
В правой части находятся три вектора, которые в сумме нулевой вектор. По правилу сложения векторов это означает, что эти вектора образуют треугольник, то есть находятся в одной плос-ти:
Значит, они компланарны. Тогда компланарны и вектора a, b и с, что противоречит условию теоремы. Значит, второго разложения р на заданные некомпланарные векторы не существует, ч. т. д.
Задание. АВСD и А1В1С1D1 – параллелограммы, располагающиеся в разных плос-тях. Докажите, что тройка векторов ВВ1, СС1 и DD1 компланарна.
Решение. Сначала построим рисунок по условию задачи:
Для доказательства используем признак компланарности векторов. Для этого надо один из векторов, отмеченных на рисунке красным, разложить на два других вектора.
В результате нам удалось разложить СС1 на вектора BB1 и CC1. Значит, эти три вектора коллинеарны.
Задание. В параллелепипеде АВСDA1B1C1D1 запишите разложение вектора BD1 по векторам ВА, ВС и ВВ1.
Решение. Сначала представим вектор BD1 как сумму трех векторов:
Теперь заметим, что вектора С1D1 и ВА соответствуют ребрам параллелепипеда. Эти ребра одинаковы по длине и параллельны, поэтому и вектора будут равными. Аналогично равны вектора СС1 и ВВ1:
Задание. АВСD – тетраэдр, а точка К делит его ребро ВС пополам. Разложите вектор DK по векторам DA, AB и AC.
Решение. Сначала запишем очевидное выражение для вектора DK:
Задание. В точке М пересекаются медианы треугольника АВС, а О – произвольная точка в пространстве. Разложите вектор ОМ по векторам ОА, ОВ и ОС.
Решение. Медиану, проходящую через точку А, мы обозначим как АА1, то есть А1 – это середина отрезка ВС. Также буквой К обозначим середину ОВ:
Сначала разложим вектор ОА1 на ОВ и ОС. Это можно сделать, ведь они компланарны. КА1 – это средняя линия ∆ОСВ, поэтому КА1||ОС и КА1 вдвое короче ОС. Это значит, что
Так как АА1 – медиана, то точка М делит ее в отношении 2:1. Отсюда вытекает следующее соотношение:
Только что решенная задача может быть использована и при решении другого, более сложного задания.
Задание. Докажите, что в параллелепипеде АВСDА1В1С1D1 плос-ти А1ВD и СB1D1 делят диагональ АС1 на три равных отрезка.
Решение. Обозначим точкой K точку пересечения медиан ∆А1ВD. Тогда по формуле, выведенной в предыдущей задаче, мы получаем, что
Это соотношение означает, что вектора АК и АС1 коллинеарны, поэтому они располагаются на одной прямой (они не могут находиться на параллельных прямых, ведь у них есть общая точка А). Значит, точка K принадлежит диагонали АС1, и отрезок АК втрое короче диагонали.
Аналогично можно показать, что и
Из этого также вытекает, что М принадлежит диагонали АС1, и МС1 втрое короче АС1. Значит, точки М и К делят диагональ на три равных отрезка, ч. т. д.
Сегодня мы расширили понятие векторов и научились их применять не только в планиметрических, но и в стереометрических задачах. При сохраняются все правила, по которым выполняются действия над векторами. Также в стереометрии появляется новое понятие компланарных и некомпланарых векторов.
📸 Видео
10 класс, 40 урок, Сложение и вычитание векторовСкачать

Что такое вектор? | Коллинеарные векторы | Сонаправленные векторы | МегаШколаСкачать

§1 ВекторыСкачать

Скалярное произведение векторов. 9 класс.Скачать

№339. Дан параллелепипед ABCDAСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

10 класс, 43 урок, Компланарные векторыСкачать

Угол между векторами. 9 класс.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

ВЕКТОРЫ решение задач 9 класс АтанасянСкачать