Одиночное число в Mathcad называется скаляром. Столбец чисел называется вектором, а прямоугольная таблица чисел — матрицей. Общий термин для вектора или матрицы — массив.
Имеются три способа создать массив:
- Заполняя массив пустых полей, как обсуждается в этом разделе. Эта методика подходит для не слишком больших массивов.
- Используя дискретный аргумент, чтобы определить элементы с его помощью, как обсуждено в следующей главе. Эта методика подходит, когда имеется некоторая явная формула для вычисления элементов через их индексы.
- Считывая их из файлов данных.
Можно различать имена матриц, векторов и скаляров, используя различный шрифт для их написания. Например, во многих математических и инженерных книгах имена векторов пишутся жирным, а имена скалярных переменных — курсивом.
Вектор — массив или матрица, содержащая один столбец. Чтобы создать вектор в Mathcad, выполните следующее:
- Щёлкните в свободном месте или на поле.
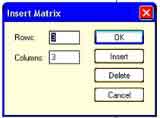
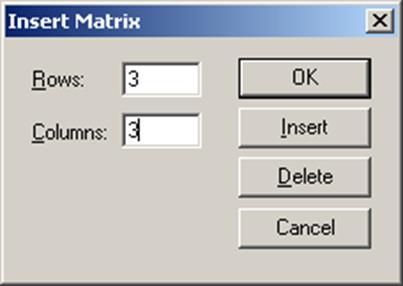
- Выберите Матрицы из меню Математика или нажмите [Ctrl]M. Появляетс я диалоговое окно, как на рисунке справа.
- Укажите число строк, равное числу элементов вектора, в поле “Строк”. Например, чтобы создать вектор с тремя элементами, напечатайте 3.
- Напечатайте 1 в поле “Столбцов”, затем нажмите “Создать”. Mathcad создает вектор с пустыми полями для заполнения.
На следующем этапе нужно заполнить эти поля скалярными выражениями. Для этого выполните следующее:
- Щёлкните на верхнем поле и напечатайте 2.
- Переместите выделяющую рамку в следующее поле. Можно сделать это или клавишей [Tab], или щёлкнув непосредственно на втором поле.
- Напечатайте 3 во втором поле. Затем переместите выделяющую рамку в третье поле, и напечатайте 4.
Если понадобится создавать еще векторы, можно оставить диалоговое окно “Матрицы” открытым для дальнейшего использования.
Как только вектор создан, можно использовать его в вычислениях в точности так же, как и число. Например, чтобы добавить другой вектор к этому вектору, необходимо выполнить следующее:
- Нажмите [ ] несколько раз или щёлкните на любой из скобок вектора. Выделяющая рамка теперь заключает весь вектор. Это означает, что знак плюс, который будет напечатан, относится к вектору целиком, а не к какому-либо из элементов.
- Нажмите клавишу плюс (+). Mathcad показывает поле для второго вектора.
- Используйте диалоговое окно “Матрицы”, чтобы создать другой вектор с тремя элементами.
- Заполните этот вектор, щелкая в каждом поле и печатая числа, показанные справа. Можно также использовать [Tab], чтобы двигаться от одного элемента к другому.
- Нажмите знак =, чтобы увидеть результат.
Сложение — только одна из операций Mathcad, определенных для векторов и матриц. В Mathcad также есть вычитание матриц, умножение матриц, скалярное произведение, целочисленные степени, детерминанты и много других операторов и функций для векторов и матриц. Полные списки появляются в разделах “Векторные и матричные операторы” и “Векторные и матричные функции” ниже в этой главе.
Если Вы используете Mathcad PLUS, Вы сможете выполнить много символьных операций с матрицами. Подробнее об этом см.в Главе “Символьные вычисления”.
Чтобы создать матрицу, сначала щёлкните в свободном месте или на поле. Затем:
- Выберите Матрицы из меню Математика, или нажмите [Ctrl]M. Появится диалоговое окно.
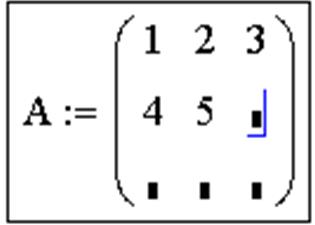
- Введите число строк и столбцов в нужные поля. В этом примере матрица имеет две строки и три столбца. Затем нажмите на “Создать”. Mathcad создаст матрицу с пустыми полями.
- В завершение заполните поля, как описано в предыдущем разделе для векторов.
Можно использовать эту матрицу в формулах в точности так же, как и число или вектор.
Везде в настоящем руководстве термин вектор относится к вектору-столбцу. Вектор-столбец идентичен матрице с одним столбцом. Можно также создать вектор-строку, создав матрицу с одной строкой и многими столбцами. Операторы и функции, которые берут векторный аргумент, всегда ожидают вектор-столбец. Они не применимы к векторам-строкам. Чтобы превратить вектор-строку в вектор-столбец, используйте оператор транспонирования[Ctrl]1.
Изменение размера матрицы
Можно изменять размер матрицы, вставляя и удаляя строки и столбцы. Для этого необходимо выполнить следующее:
- Щёлкните на одном из элементов матрицы, чтобы заключить его в выделяющую рамку. Mathcad будет начинать вставку или удаление с этого элемента.
- Выберите Матрицы из меню Математика. Появляется диалоговое окно.
- Напечатайте число строк и-или столбцов, которые нужно вставить или удалить. Затем нажмите на “Вставить” или на “Удалить”. Например, чтобы удалить столбец, который содержит выбранный элемент, напечайте 1 в поле “Столбцов”, 0 в поле “Строк”, и нажмите на “Удалить”.
Вот как Mathcad будет удалять или вставлять строки или столбцы, в зависимости от того, что впечатывается в диалоговое окно:
- Если вставляются строки, Mathcad создает строки пустых полей ниже выбранного элемента. Если вставляются столбцы, Mathcad создает столбцы пустых полей справа от выбранного элемента.
- Чтобы вставить строку выше верхней строки или столбец слева от первого столбца, сначала заключите матрицу целиком в выделяющую рамку, щёлкнув внутри и нажав [ ] несколько раз. Затем выберите Матрицы и продолжите, как обычно.
- Когда строки или столбцы удаляются, Mathcad начинает со строки или столбца, занятых выбранным элементом. Mathcad удаляет строки вниз от этого элемента и столбцы — направо от этого элемента.
- Если напечатать 0 в поле “Строк”, Mathcad ни вставит, ни удалит строки. Если напечатать 0 в поле “Столбцов”, Mathcad ни вставит, ни удалит столбцы.
Обратите внимание, что при удалении строк или столбцов Mathcad выбрасывает содержащуюся в них информацию.
Чтобы удалить всю матрицу или вектор, заключите их в выделяющую рамку и выберите Вырезать из меню Правка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

Векторы и матрицы в MathCAD
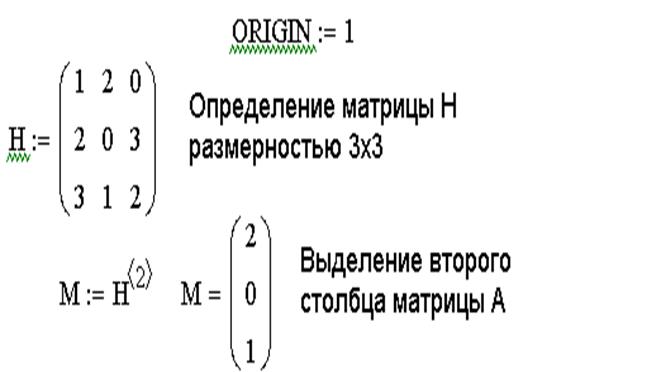
Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.
Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.
Поэлементный ввод массива Х
| Вводимые символы | Отображаемые символы |
| X [ 1 Shift+: 5 | X1:=5 |
| X [ 2 Shift+: 8 | X2:= 8 |
| X [ 3 Shift+: 10 | X3:= 10 |
Поэлементный ввод матрицы А
| Вводимые символы | Отображаемые символы |
| A [ 1,1 Shift+: 0.1 | A11 := 0.1 |
| A [ 1,2 Shift+: -2.5 | A12 := -2.5 |
| A [ 2,1 Shift+: -1.0 | A21 := -1.0 |
| A [ 2,2 Shift+: 5.2 | A22 := 5.2 |
Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке 
ПанельMatrix содержит следующие кнопки:









Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки 
1. Ввести с клавиатуры имя матрицы и знак присваивания;
2. Щелчком по кнопке 
3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;
4. Закрыть окно диалога, щелкнув по кнопке OK;
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:
Функции определения матриц и операции с блоками матриц:
matrix(m,n,f) – создает и заполняет матрицу A=<aij> размерности m на n, каждый элемент которой aij равен значению функции f(i,j);
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число строк);
stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l
Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;
Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;
Функции вычисления различных числовых характеристик матриц:
last(v) – вычисление номера последнего элемента вектора v;
length(v) – вычисление количества элементов вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице (векторе) А;
min(A) – вычисление наименьшего элемента в матрице (векторе) А;
mean(A) – вычисление среднего значения матрицы (вектора) А;
tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;
ranc(A) – вычисление ранга матрицы А;
Функции, реализующие численные алгоритмы:
rref(A) – приведение матрицы А к ступенчатому виду;
geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;
lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.
lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;
qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;
cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙L T , где А — квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;
sort(v) – сортировка элементов вектора v в порядке возрастания их значений;
reverse(v) – перестановка элементов вектора v в обратном порядке;
csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;
rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.
ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.
ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.
ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.
ЗАДАЧА 4. Элементы матрицы формируются по формуле 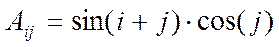
ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:
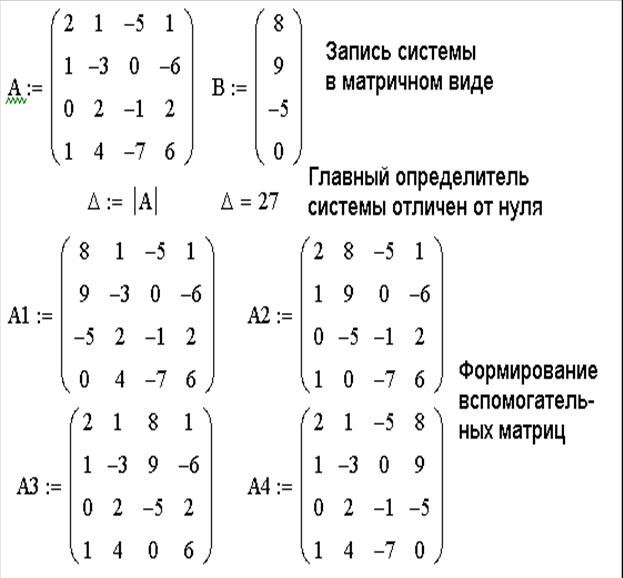
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:
Для решения поставленной задачи необходимо выполнить следующие действия:
1. Сформировать матрицу системы А и вектор правых частей b.
2. Вычислить главный определитель ∆.
3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆i;
4. Вычислить определители ∆i;
5. Найти решение системы по формуле xi=∆i/∆.
ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.
1. Сформировать матрицу коэффициентов и вектор свободных членов системы.
2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.
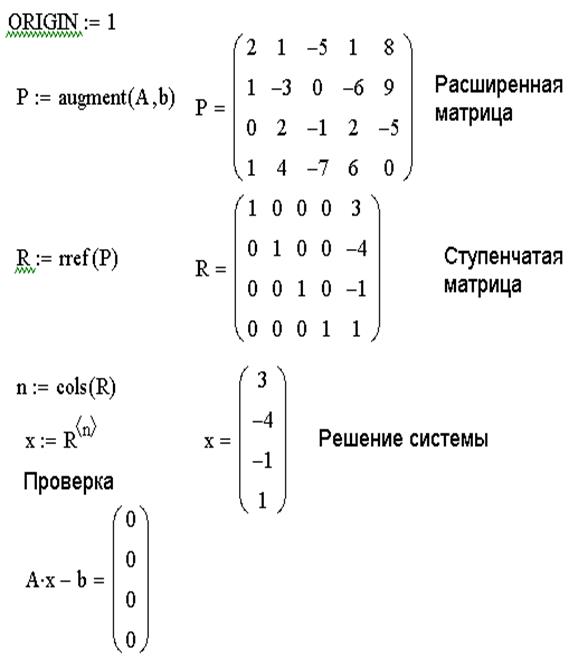
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.
Порядок решения задачи:
1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.
2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);
3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.
4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.
5. Выполнить проверку Ax-B=0.
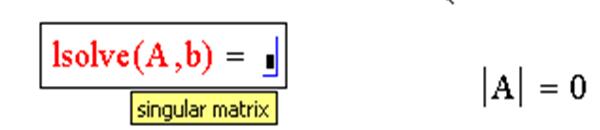
ЗАДАЧА 9. Решить систему при помощи функции lsolve:
Пример системы, которая не имеет решений:
Пример системы, которая имеет бесконечное множество решений
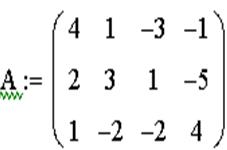
ЗАДАЧА 10. Решить систему при помощи решающего блока.
Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.
Правее и ниже ключевого слова записываются уравнения системы.
Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.
Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.
Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).
Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).
Видео:Mathcad. Вывести таблицу и графикСкачать

Из таблицы в вектор маткад
БАЗОВЫЕ ОПЕРАЦИИ.
РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ
МАССИВЫ
1 Запуск. Формульные и текстовые области
Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:
Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).
Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!
Перемещение курсора — клавиша Пробел. Изменение направления уголка — клавиша Insert (Ins).
«:=» — «присвоить» — задать выражение (число или формулу)
«=» — «вычислить» подсчитать и вывести значение выражения.
Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.
2 Ранжированные переменные. Функции. Графики
В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.
Ранжированная переменная общего вида определяется выражением:
Имя := x1, x2 .. xn
Здесь Имя – задаваемое пользователем имя ранжированной переменной;
x1 – первое значение ранжированной переменной;
x2 – второе значение ранжированной переменной (x2 = x1 + Dx — первое значение плюс шаг);
xn – последнее значение ранжированной переменной.
Значения x1 и x2 разделяются запятой, двоеточие представляет собой единый оператор, указывающий на изменение переменной в заданных пределах. Он вводится с клавиатуры клавишей «;» или выбирается с палитры математических инструментов Matrix (Векторы и матрицы) (кнопка 
Например, если переменная изменяется в интервале 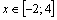
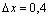
Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.
Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку 
Среди наиболее часто используемых функций можно указать:
- sin(z) — синус z (z задается в радианах);
- cos(z) — косинус z;
- tan(z) — тангенс z;
- cot(z) — котангенс z;
- exp(z) – экспоненциальная функция, значение е (основание натурального логарифма) в степени z;
- ln(z) – натуральный логарифм z;
- log(z) – десятичный логарифм числа z;
- log(z, b) – логарифм числа z по основанию b;
- acos(z) – арккосинус z;
- acot(z) – арккотангенс z;
- asin(z) – арксинус z;
- atan(z) – арктангенс z.
Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется
Имя(список аргументов) := Выражение
Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.
Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.
Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).
Для построения графика функции одной переменной в декартовой системе координат в Mathcad:
- определяется функция пользователя;
- задается ранжированная переменная на некотором диапазоне с мелким шагом;
- вставляется шаблон двумерного графика X-Y Plot
;
- в знакоместо по оси абсцисс записывается имя переменной, а в знакоместо по оси ординат — функция или имя ранее определенной функции;
- производится щелчок левой клавишей мыши вне области графика.
Примечание — Для построения в одной координатной плоскости графиков двух и более функций их имена или определяющие выражения перечисляются в знакоместе по оси ординат через запятую.
Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

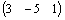
Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:
Существует несколько способов создания массивов.
1-й способ. Использование панели Matrix (Матрицы).
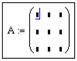
Сначала набирается имя массива и оператор присваивания, например, 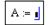
Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.
На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:
2-й способ. Использование ранжированной переменной.
Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:
- определяется системная переменная ORIGIN;
- задается ранжированная переменная (переменные) для нумерации элементов;
- индексированной переменной присваиваются значения элементов массива через запятую или в виде явной формулы.
Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма 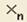
Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.
Таблица 1 – Команды палитры инструментов Matrix (Матрица)
📺 Видео
7. MathCad. Векторы и матрицыСкачать

Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать
Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

Математика это не ИсламСкачать

Оператор векторизации в MathCAD 14 (23/34)Скачать

Дискретные переменные в MathCAD 14 (9/34)Скачать

МАТКАД МатрицыСкачать
19 Циклы в Mathcad while, for, построить таблицу с цифрами в Маткаде, примеры с предусловиемСкачать

2. Дискретная переменная. Построение таблиц (Азы понимания пк Mathcad)Скачать

PTC Mathcad Prime 3.0 - Excel ComponentsСкачать

Векторы и матрицыСкачать
Программа MathCAD. Урок 10. Работа с матрицами в MathCADСкачать

Урок 8. МКЭ в Mathcad. Векторы концевых усилийСкачать

Основы работы в Mathcad ГрафикиСкачать

Урок 7. МКЭ в Mathcad. Матрицы инциденций, жесткости и вектор перемещений ДМСкачать
Матрицы и векторы. Настройки Mathcad при работе с матрицами. Урок 12Скачать

MathCad компланарность векторов.wmvСкачать

Работа с массивами. Вектор столбцы и вектор строки 2. Урок 8Скачать

















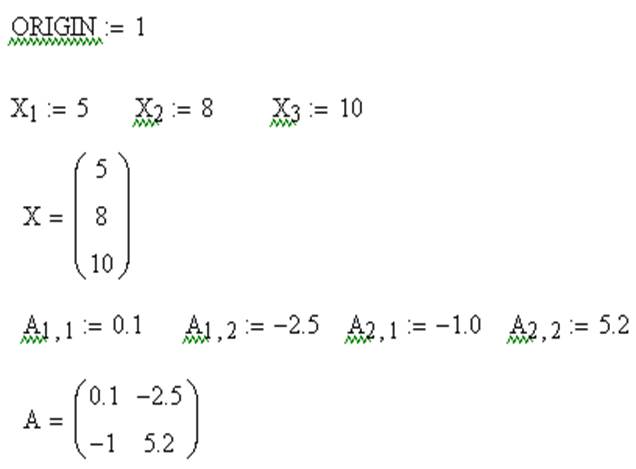


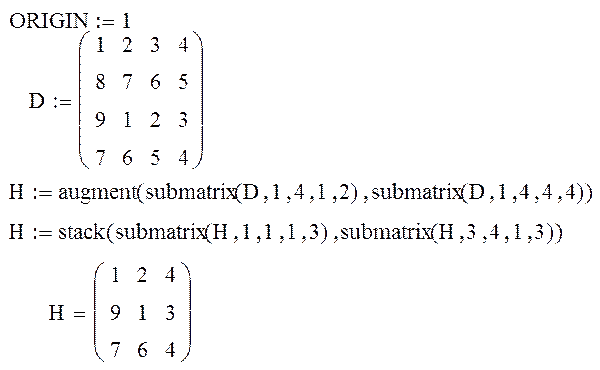
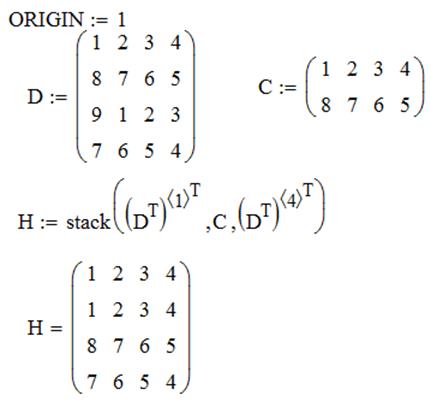
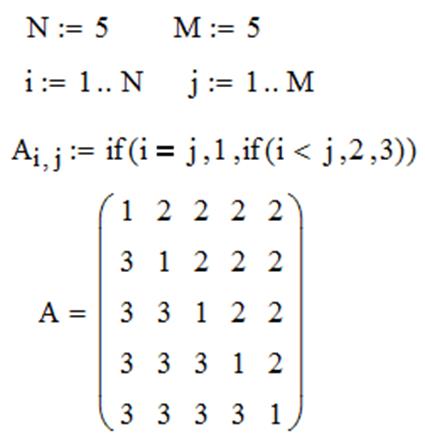

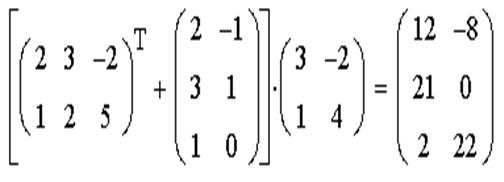


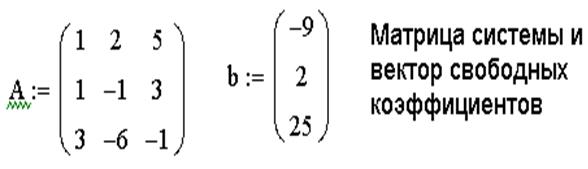

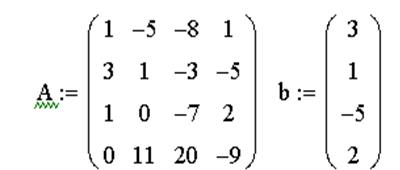
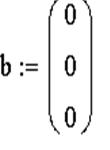


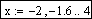
 ;
;