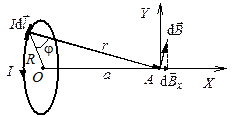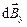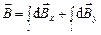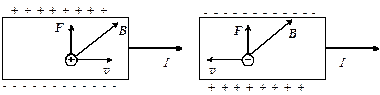Индукция магнитного поля в центре окружности (6 видео)

Индукция магнитного поля в центре и на оси кругового витка с током

Вначале решим более общую задачу нахождения магнитной индукции на оси витка с током. Для этого сделаем рисунок 3.8, на котором изобразим элемент тока 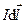и вектор магнитной индукции , который он создает на оси кругового контура в некоторой точке .

Рис. 3.8 Определение магнитной индукции

на оси кругового витка с током

Вектор магнитной индукции , создаваемый бесконечно малым элементом контура может быть определен с помощью закона Био-Савара-Лапласа (3.10).

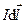
Как следует из правил векторного произведения, магнитная индукция будет перпендикулярна плоскости, в которой лежат вектора и , поэтому модуль вектора будет равен

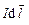
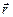
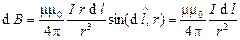
Для нахождения полной магнитной индукции от всего контура необходимо векторно сложить от всех элементов контура, т. е. фактически сосчитать интеграл по длине кольца

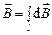
Данный интеграл можно упростить, если представить в виде суммы двух составляющих и

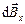
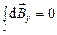
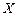
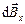
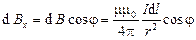
При этом в силу симметрии , поэтому результирующий вектор магнитной индукции будет лежать на оси . Следовательно, для нахождения модуля вектора нужно сложить проекции всех векторов , каждая из которых равна

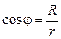
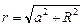
Учитывая, что и , получим для интеграла следующее выражение

. (3.18)

Нетрудно заметить, что вычисление получившегося интеграла даст длину контура, т. е. 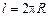. В итоге суммарная магнитная индукция, создаваемая круговым контуром на оси в точке , равна

. (3.19)

Используя магнитный момент контура, формулу (3.19) можно переписать следующим образом

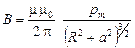
Теперь отметим, что полученное в общем виде решение (3.19) позволяет проанализировать предельный случай, когда точка помещена в центре витка. В этом случае и решение для магнитной индукции поля в центре кольца с током примет вид

. (3.20)

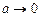
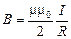
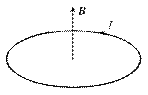
Результирующий вектор магнитной индукции (3.19) направлен вдоль оси тока, а его направление связано с направлением тока правилом правого винта (рис. 3.9).

Рис. 3.9 Определение магнитной индукции

в центре кругового витка с током

Индукция магнитного поля в центре дуги окружности

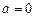
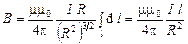
Данная задача может быть решена как частный случай рассмотренной в предыдущем пункте задачи. В этом случае интеграл в формуле (3.18) следует брать не по всей длине окружности, а только по ее дуге l. А также учесть то, что индукция ищется в центре дуги, поэтому . В результате получим

, (3.21)

где 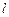– длина дуги; – радиус дуги.

5 Вектор индукции магнитного поля движущегося в вакууме точечного заряда (без вывода формулы)

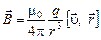
где 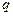– электрический заряд; – постоянная нерелятивистская скорость; – радиус-вектор, проведенный от заряда к точке наблюдения.

Силы Ампера и Лоренца

Опыты по отклонению рамки с током в магнитном поле показывают, что на всякий проводник с током, помещенный в магнитное поле, действует механическая сила, называемая силой Ампера.

Закон Ампера определяет силу, действующую на проводник с током, помещенный в магнитное поле:

; , (3.22)

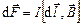
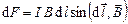
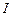
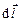
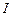
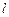
где – сила тока; – элемент длины провода (вектор совпадает по направлению с током ); – длина проводника. Сила Ампера перпендикулярна направлению тока и направлению вектора магнитной индукции.

Если прямолинейный проводник длиной 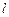находится в однородном поле, то модуль силы Ампера определяется выражением (рис. 3.10):

. (3.23)

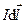
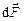
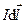
Сила Ампера всегда направлена перпендикулярно плоскости, содержащей векторы и , а ее направление как результат векторного произведения определяется правилом правого винта: если смотреть вдоль вектора , то поворот от к по кратчайшему пути должен происходить по часовой стрелке.

Рис. 3.10 Правило левой руки и правило буравчика для силы Ампера

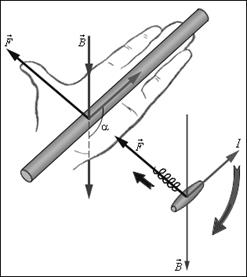
С другой стороны, для определения направления силы Ампера можно также применить мнемоническоеправило левой руки (рис. 3.10): нужно поместить ладонь так, чтобы силовые линии магнитной индукции входили в нее, вытянутые пальцы показывали направление тока, тогда отогнутый большой палец укажет направление силы Ампера.

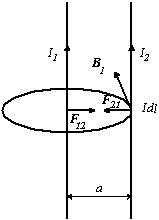
Исходя из формулы (3.22), найдем выражение для силы взаимодействия двух бесконечно длинных, прямых, параллельных друг другу проводников, по которым текут токи I₁ и I₂ (рис. 3.11) (опыт Ампера). Расстояние между проводами равно a.

Определим силу Ампера dF₂₁, действующую со стороны магнитного поля первого тока I₁ на элемент l₂dl второго тока.

Величина магнитной индукции этого поля B₁ в точке расположения элемента второго проводника с током равна

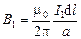
Рис. 3.11 Опыт Ампера по определению силы взаимодействия

двух прямолинейных токов

Тогда с учетом (3.22) получим

. (3.24)

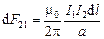
Рассуждая точно так же, можно показать, что сила Ампера, действующая со стороны магнитного поля, создаваемого вторым проводником с током, на элемент первого проводника I₁dl , равна

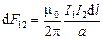
т. e. dF₁₂ = dF₂₁. Таким образом, мы вывели формулу (3.1), которая была получена Ампером экспериментальным путем.

На рис. 3.11 показано направление сил Ампера. В случае, когда токи направлены в одну и ту же сторону, то это ‑ силы притяжения, а в случае токов разного направления ‑ силы отталкивания.

Из формулы (3.24), можно получить силу Ампера, действующую на единицу длины проводника

. (3.25)

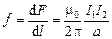
Таким образом, сила взаимодействия двух параллельных прямых проводников с токами прямо пропорциональна произведению величин токов и обратно пропорциональна расстоянию между ними.

Закон Ампера утверждает, что на элемент с током, помещенный в магнитное поле, действует сила. Но всякий ток есть перемещение заряженных частиц. Естественно предположить, что силы, действующие на проводник с током в магнитном поле, обусловлены силами, действующими на отдельные движущиеся заряды. Этот вывод подтверждается рядом опытов (например, электронный пучок в магнитном поле отклоняется).

Найдем выражение для силы, действующей на заряд, движущийся в магнитном поле, исходя из закона Ампера. Для этого в формулу, определяющую элементарную силу Ампера

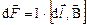
подставим выражение для силы электрического тока

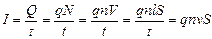
где I – сила тока, протекающего через проводник; Q – величина полного заряда протекшего за время t; q – величина заряда одной частицы; N – общее число заряженных частиц, прошедших через проводник объемом V, длиной l и сечением S; n – число частиц в единице объема (концентрация); v – скорость частицы.

В результате получим:

. (3.26)

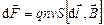
Направление вектора совпадаёт с направлением скорости v, поэтому их можно поменять местами.

. (3.27)

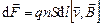
Эта сила действует на все движущиеся заряды в проводнике длиной и сечением S, число таких зарядов:

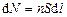
Следовательно, сила, действующая на один заряд, будет равна:

. (3.28)

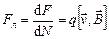
Формула (3.28) определяет силу Лоренца, величина которой

, (3.29)

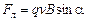
где a — угол между векторами скорости частицы и магнитной индукции.

В экспериментальной физике часто встречается ситуация, когда заряженная частица движется одновременно и в магнитном и электрическом поле. В этом случае рассматривают полную силу Лоренца в виде

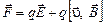
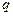
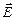
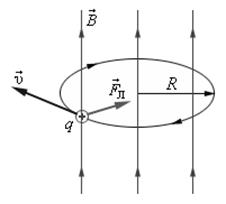
где – электрический заряд; – напряженность электрического поля; – скорость частицы; – индукция магнитного поля.

Только в магнитном поле на движущуюся заряженную частицу действует магнитная составляющая силы Лоренца (рис. 3.12)

. (3.30)

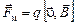
Рис. 3.12 Сила Лоренца

Магнитная составляющая силы Лоренца перпендикулярна вектору скорости и вектору магнитной индукции. Она не изменяет величины скорости, а изменяет только ее направление, следовательно, работы не совершает.

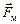
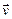
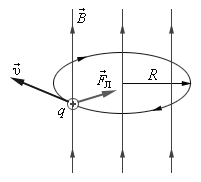
Взаимная ориентация трех векторов ‑ , и , входящих в (3.30), показана на рис. 313 для положительно заряженной частицы.

Рис. 3.13 Сила Лоренца, действующая на положительный заряд

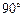
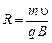
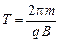
Как видно из рис. 3.13, если частица влетает в магнитное поле под углом к силовым линиям , то она равномерно движется в магнитном поле по окружности радиусом и периодом обращения:

; ,

где 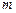– масса частицы.

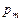
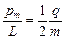
Отношение магнитного момента к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите,

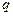
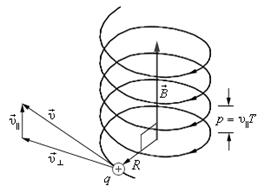
где ‑ заряд частицы; т ‑ масса частицы.

Рассмотрим общий случай движения заряженной частицы в однородном магнитном поле, когда ее скорость направлена под произвольным углом a к вектору магнитной индукции (рис. 3.14). Если заряженная частица влетает в однородное магнитное поле под углом 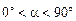, то она движется по винтовой линии.

Разложим вектор скорости на составляющие v_|| (параллельную вектору ) и v_^(перпендикулярную вектору ):

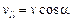
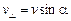
Наличие v_^ приводит к тому, что на частицу будет действовать сила Лоренца и она будет двигаться по окружности радиусом R в плоскости перпендикулярной вектору :

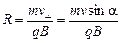
Период такого движения (время одного витка частицы по окружности) равен

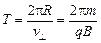
Рис. 3.14 Движение по винтовой линии заряженной частицы

в магнитном поле

За счет наличия v_|| частица будет двигаться равномерно вдоль , так как на v_|| магнитное поле не действует.

Таким образом, частица участвует одновременно в двух движениях. Результирующая траектория движения представляет собой винтовую линию, ось которой совпадает с направлением индукции магнитного поля. Расстояние h между соседними витками называется шагом винтовой линии и равно:

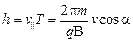
Действие магнитного поля на движущийся заряд находит большое практическое применение, в частности, в работе электронно-лучевой трубки, где используется явление отклонения заряженных частиц электрическим и магнитным полями, а также в работе масс-спектрографов, позволяющих определить удельный заряд частиц (q/m) и ускорителей заряженных частиц (циклотронов).

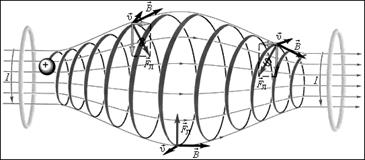
Рассмотрим один такой пример, назыаемый «магнитной бутылкой» (рис. 3.15). Пусть неоднородное магнитное поле создано двумя витками с токами, протекающими в одном направлении. Сгущение линий индукции в какой-либо пространнственной области означает большее значение величины магнитной индукции в этой области. Индукция магнитного поля вблизи витков с током больше, чем в пространстве между ними. По этой причине радиус винтовой линии траектории частицы, обратно пропорциональный модулю индукции, меньше вблизи витков, чем в пространстве между ними. 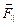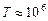После того, как частица, двигаясь вправо по винтовой линии, пройдет среднюю точку, сила Лоренца, действующая на чатицу, приобретает компоненту , тормозящую ее движение вправо. В определенный момент эта компонента силы останавливает движение частицы в этом направлении и отталкивает ее влево к витку 1. При приближении заряженной частицы к витку 1 она также тормозится и начинает циркулировать между витками, оказавшись в магнитной ловушке, или между «магнитными зеркалами». Магнитные ловушки используются для удержания в определенной области пространства высокотемпературной плазмы ( К) при управляемом термоядерном синтезе.

Рис. 3.15 Магнитная «бутылка»

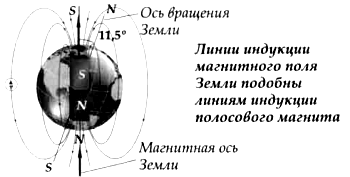
Закономерностями движения заряженных частиц в магнитном поле можно объяснить особенности движения космических лучей вблизи Земли. Космические лучи – это потоки заряженных частиц большой энергии. При приближении к поверхности Земли эти частицы начинают испытывать действие магнитного поля Земли. Те из них, которые направляются к магнитным полюсам, будут двигаться почти вдоль линий земного магнитного поля и навиваться на них. Заряженные частицы, подлетающие к Земле вблизи экватора, направлены почти перпендикулярно к линиям магнитного поля, их траектория будет искривляться. и лишь самые быстрые из них достигнут поверхности Земли (рис. 3.16).

Рис. 3.16 Образование Полярного сияния

Поэтому интенсивность космических лучей доходящих до Земли вблизи экватора, заметно меньше, чем вблизи полюсов. С этим связан тот факт что, Полярное сияние наблюдается главным образом в приполярных областях Земли.

Эффект Холла

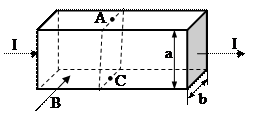
В 1880г. американский физик Холл провел следующий опыт: он пропускал постоянный электрический ток I через пластинку из золота и измерял разность потенциалов между противолежащими точками A и C на верхней и нижней гранях (рис. 3.17).

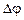
Рис. 3.17 Эффект Холла

В отсутствии магнитного поля 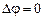, т. к. для однородной пластины поперечное сечение является эквипотенциальной поверхностью. Когда пластины помещаются в однородное магнитное поле с индукцией , перпендикулярное к ее боковым граням ‑ между точками A и C возникала разность потенциалов. Это явление было позднее названо эффектом Холла.

Экспериментально было обнаружено, что

, (3.31)

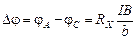
где I ‑ сила тока; B ‑ индукция магнитного поля; b ‑ ширина пластины; 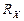‑ постоянная Холла.

Дальнейшее исследование показало, что эффект Холла наблюдается во всех проводниках и полупроводниках. Величина константы Холла зависит от материала пластины, причем этот коэффициент для одних веществ положителен, а для других ‑ отрицателен.

Явление Холла можно объяснить, исходя из силы Лоренца. На заряд, движущийся в магнитном поле с индукцией B, действует сила Лоренца

Рис. 3.18 Знак эффекта Холла

Если носителями тока в веществе являются положительные заряды то под действием силы Лоренца эти заряды q отклоняются к верхней грани (при выбранных направлениях и ). Следовательно, вблизи верхней грани возникнет избыток зарядов, а вблизи нижней грани – недостаток зарядов, т. е. возникает разность потенциалов. В случае отрицательных зарядов, как видно из рисунка 3.18, знак разности потенциалов будет противоположым.

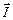
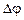
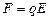
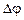
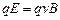
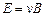
Найдем теперь выражение для . При возникновении разности потенциалов в пластине возникает электрическое поле в вертикальном направлении. Со стороны этого электрического поля на заряд q будет действовать сила , направленная против силы Лоренца. При некотором значении эти силы уравновесят друг друга, и установится равновесный процесс прохождения тока

.(3.32)

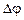
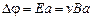
Если пластина достаточно длинная и широкая, то поперечное электрическое поле можно считать однородным. Для однородного поля можно написать связь между E и в виде:

. (3.33)

Силу тока I можно выразить следующим образом:

, (3.34)

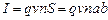
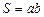
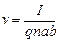
где v ‑ скорость упорядоченного движения зарядов; n ‑ число зарядов в единице объема; – площадь поперечного сечения пластины.

, (3.35)

подставляя (3.35) в (3.33) получим

. (3.36)

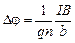
Сравнивая эту формулу с экспериментальной (3.31), имеем

. (3.37)

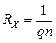
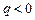
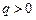
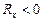
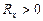
Отсюда видно, что, знак константы Холла совпадает со знаком заряда q носителей тока. В полупроводниках носителями тока могут быть электроны ( ) и положительные дырки ( ). На основании измерения константы Холла для полупроводников можно судить о природе его проводимости. При электронной проводимости , при дырочной проводимости .

С помощью константы Холла можно также определить концентрацию носителей тока, если характер проводимости и заряд носителей тока известны (например, для металлов):

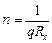
На принципе, похожем на эффект Холла, основана работа МГД- генераторов (магнитогидродинамических генераторов). В эффекте Холла используется ток проводимости, а можно использовать конвекционный ток. Например, по трубе продувается поток раскаленных газов (следовательно, ионизированных) в магнитном поле. В трубу вводятся электроды, на них возникает разность потенциалов. Величина 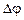оказывается пропорциональной скорости движения газа. Для увеличения электропроводимости должна быть велика концентрация ионов n, что можно достигнуть повышением температуры газа. Кроме того, в поток газа вводятся специальные присадки ‑ элементы с малой энергией ионизации.

К.П.Д. МГД-генераторов может достигать 50…60%, в то время, как у тепловых электростанций 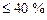. Также преимуществом МГД-генераторов является то, что в них нет никаких механических движущихся частей и, следовательно, потерь на преодоление трения.

Содержание

Магнитное поле кругового тока
Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока
Готовые работы на аналогичную тему
Магнитное поле кругового тока в его центре
Кольца Гельмгольца
Магнитное поле и его характеристики
теория по физике 🧲 магнетизм
Основные свойства магнитного поля
Вектор магнитной индукции
Напряженность магнитного поля
Направление вектора магнитной индукции и способы его определения
Магнитное поле прямолинейного тока
Магнитное поле кругового тока
Магнитное поле электромагнита (соленоида)
Алгоритм определения полярности электромагнита
🔍 Видео

Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

Магнитное поле кругового тока

Вы будете перенаправлены на Автор24

Французские ученые Ж. Био и Ф. Савар изучали магнитные поля, создаваемые постоянными токами разной формы. Результаты их работы обобщил известный математик и физик П. Лаплас.

Видео:Магнитное поле. Магнитная индукция | Физика 11 класс #1 | ИнфоурокСкачать

Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока

Закон Био-Савара–Лапласа описывает порождение магнитного поля током $I$ на элементе проводника длиной $dl$ в некоторой точке пространства ($mu$ — магнитная проницаемость вещества в котором локализовано поле):

где $d vec l ⃗$ — вектор, длина которого равна длине элемента проводника $dl$, направленный по току; $vec r$ – радиус-вектор, который проведен от элемента $dl$ в точку, в которой исследуется магнитное поле. Поскольку в правой части формулы (1) находится векторное произведение, очевидно, что индукция элементарного магнитного поля будет направлена перпендикулярно плоскости, в которой находятся векторы $vec r$ и $vec l$ и при этом является касательной к силовой линии поля.

Величину вектора $vec$ из выражения (1) найдем как:

где $ alpha $– угол между векторами $vec r$ и $vec l$ .

Конкретное направление $vec$ находят по правилу буравчика (правилу правой руки):

Если правый винт вращать так, что его поступательное движение будет совпадать с направлением течения тока в избранном элементе, то вращение его головки укажет направление $vec$.

Магнитные поля подчиняются принципу суперпозиции:

Суммарную магнитную индукцию поля, создаваемого несколькими источниками, находят как геометрическую сумму векторов магнитной индукции отдельных полей:

$vec=sumlimits_^N vec_ left( 3 right). $

Если распределение токов можно считать непрерывным, то принцип суперпозиции можно записать:

Вычисление магнитной индукции поля с применением закона Био-Савара-Лапласа довольно сложная процедура. Но при существовании определенной симметрии в распределении токов, используя, рассмотренный нами закон и принцип суперпозиции, рассчитать конкретные поля просто. В любом случае следует придерживаться следующей схемы действий:

Готовые работы на аналогичную тему

Выделить на проводнике с током элементарный отрезок $dl$.
Записать для исследуемой точки поля закон Био – Савара – Лапласа.
Определить направление элементарного поля $vec$ в избранной точке.
Воспользоваться принципом суперпозиции для магнитных полей (учесть, что суммируются векторы).

Видео:Физика 9 класс (Урок№19 - Индукция магнитного поля.)Скачать

Магнитное поле кругового тока в его центре

Рисунок 1. Магнитное поле кругового тока в его центре. Автор24 — интернет-биржа студенческих работ

Рассмотрим круговой проводник, по которому течет постоянный ток $I$ (рис.1). Выделим на этом проводнике элемент $dl$, который можно считать прямолинейным. Если перейти к другому элементу этого же тока, затем к третьему и так далее, применить правило правого винта, то очевидно, что все магнитные поля, созданные этими элементами в центре, направлены вдоль одной прямой, перпендикуляру к плоскости кольца. Это означает, применяя принцип суперпозиции, мы векторное сложение заменим алгебраическим.

Запишем закон Био-Савара-Лапласа для модуля вектора индукции поля, создаваемого элементом d$l_1$:

Из рис.1 мы видим:

что расстояние от элементарного тока до центра витка равно его радиусу ($R$) и будет одинаковым для всех элементов на этом витке,
элемент $dl$ (как и все остальные элементы) будут нормальны к радиус-вектору $vec r$.

Учитывая сказанное выражение (5) представим в виде:

Обезличивая витки с током, положим далее $dl_1=dl$.

Поскольку наш ток является непрерывным, то для нахождения полного поля в его центре, мы проинтегрируем (6), имеем:

$L=2πR$ — длина окружности витка.

Индукция магнитного поля кругового тока на его оси

Найдем индукцию магнитного поля на оси кругового тока, если ток, текущий по нему равен $I$, радиус витка — $R$ (рис.2).

Рисунок 2. Индукция магнитного поля кругового тока на его оси. Автор24 — интернет-биржа студенческих работ

Как основу для выполнения поставленной задачи возьмем закон Био-Савара-Лапласа (1), где из рис.2 мы видим, что:

$dvectimes vec=dvectimes vec+dvectimes vec(9).$

Используя принцип суперпозиции закон (1) для нашего тока и формулы (8-9) запишем:

В выражении (10) при записи интеграла, мы учли, что величина вектора $vec$ не изменяется. Кроме этого вектор $vec h$, определяющий положение точки, в которой мы ищем поле, не изменяется при движении по нашему контуру, поэтому:

$ointlimits_L <dvectimes vec> =(ointlimits_L <dvec)timesvec> =0, left( 11 right),$

так как ( $ointlimits_L <dvec)=0.>$

Вычислим интеграл: $ointlimits_L <dvectimes vec.>$ Введем единичный вектор ($vec n$), нормальный к плоскости витка с током.

$ointlimits_L <dvectimes vec=ointlimits_L <vecRdl=vecR>> ointlimits_L <dl=vecR> 2pi R=2pi R^vecleft( 12 right)$.

Подставляем результаты интегрирования из (12) в (10), имеем:

где при записи окончательного результата мы учли, что:

Видео:Как магнитное поле назвали магнитной индукциейСкачать

Кольца Гельмгольца

Кольцами Гельмгольца считают пару проводников в виде колец одного радиуса, расположенных в параллельных плоскостях (рис.3) на одной оси. Расстояние между плоскостями колец равно их радиусу.

Рисунок 3. Кольца Гельмгольца. Автор24 — интернет-биржа студенческих работ

Рассмотрим магнитное поле на оси этих колец.

Декартову систему координат разместим так, что ее начало совпадает с центром нижнего кольца с током. Ось Z нашей системы будет направлена по оси колец (рис.3).

Запишем индукцию магнитного поля в точке с координатой $z$ на оси колец. Используем формулу (13):

Исследуем полученное поле. Считается, что магнитное поле на оси колец Гельмгольца на посередине между ними является однородным.

Неоднородность в первом приближении характеризуют первой производной:

Если $z=fracquad$ , подставим в (15), имеем:

По условию для колец Гельмгольца, имеем: $d=R.$

На середине их общей оси ($z=frac)$, получаем:

Равенство нулю второй производной от $B_z$ по координате $z$, показывает, что в на середине оси колец магнитное поле является однородным с высокой степенью точности.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 28 03 2022

Видео:Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Магнитное поле и его характеристики

теория по физике 🧲 магнетизм

Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.

Основные свойства магнитного поля

Магнитное поле порождается электрическим током (движущимися зарядами).
Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
Магнитное поле существует независимо от нас, от наших знаний о нем.

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Вектор магнитной индукции

Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как → B . Единица измерения — Тесла (Тл).

За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.

Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:

B = F A m a x I l . .

За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.

Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.

Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.

Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.

Видео:Магнитное поле соленоидаСкачать

Напряженность магнитного поля

Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как → H . Единица измерения — А/м.

μ — магнитная проницаемость среды (у воздуха она равна 1), μ 0 — магнитная постоянная, равная 4 π · 10 − 7 Гн/м.

Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: → H ↑↑ → B .

Видео:ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ сила Ампера правило левой рукиСкачать

Направление вектора магнитной индукции и способы его определения

Чтобы определить направление вектора магнитной индукции, нужно:

Расположить в магнитном поле компас.
Дождаться, когда магнитная стрелка займет устойчивое положение.
Принять за направление вектора магнитной индукции направление стрелки компаса «север».

В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:

При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:

При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора → B магнитной индукции.

Отсюда следует, что:

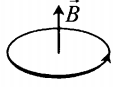
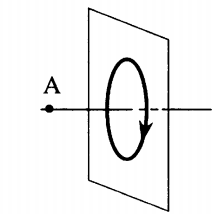
Если по витку ток идет против часовой стрелки, то вектор магнитной индукции → B направлен вверх.

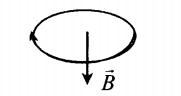
Если по витку ток идет по часовой стрелке, то вектор магнитной индукции → B направлен вниз.

Способы обозначения направлений векторов:

Вверх
Вниз
Влево
Вправо
На нас перпендикулярно плоскости чертежа
От нас перпендикулярно плоскости чертежа

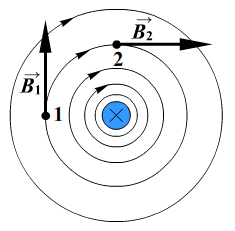
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?

Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Магнитное поле прямолинейного тока

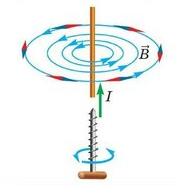
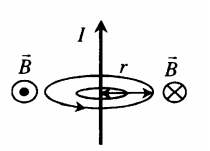
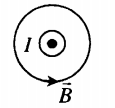
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.

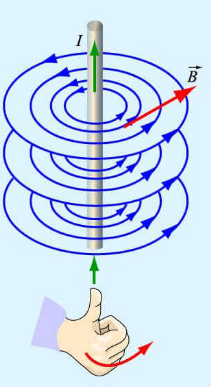
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:

Правило буравчика (правой руки)

Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.

Модуль вектора магнитной индукции на расстоянии r от оси проводника:

B = μ μ 0 I 2 π r . .

Магнитное поле кругового тока

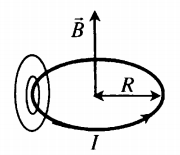
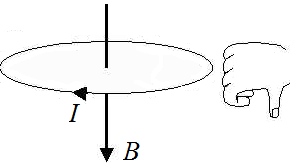
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.

Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:

Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.

Модуль вектора магнитной индукции в центре витка, радиус которого равен R:

Модуль напряженности в центре витка:

Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?

Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.

Видео:Индукция магнитного поляСкачать

Магнитное поле электромагнита (соленоида)

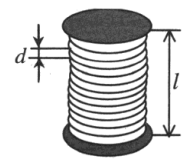
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.

Число витков в соленоиде N определяется формулой:

l — длина соленоида, d — диаметр проволоки.

Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.

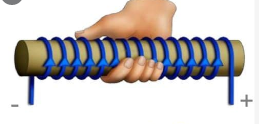
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции → B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.

Модуль вектора магнитной индукции в центральной области соленоида:

B = μ μ 0 I N l . . = μ μ 0 I d . .

Модуль напряженности магнитного поля в центральной части соленоида:

H = I N l . . = I d . .

Алгоритм определения полярности электромагнита

Определить полярность источника.
Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
Определить направление вектора магнитной индукции.
Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).

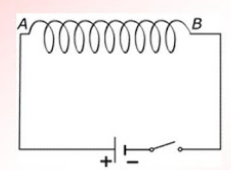
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.

Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.

На рисунке изображён круглый проволочный виток, по которому течёт электрический ток. Виток расположен в вертикальной плоскости. В центре витка вектор индукции магнитного поля тока направлен

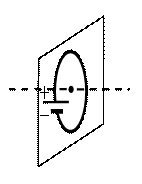
а) вертикально вверх в плоскости витка

б) вертикально вниз в плоскости витка

в) вправо перпендикулярно плоскости витка

г) влево перпендикулярно плоскости витка

Алгоритм решения

Решение

По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора → B магнитной индукции мы будем использовать правило правой руки.

Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.

Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Магнитная стрелка компаса зафиксирована на оси (северный полюс затемнён, см. рисунок). К компасу поднесли сильный постоянный полосовой магнит и освободили стрелку. В каком положении установится стрелка?

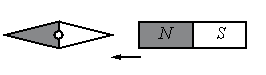
а) повернётся на 180°

б) повернётся на 90° по часовой стрелке

в) повернётся на 90° против часовой стрелки

г) останется в прежнем положении

Алгоритм решения

Вспомнить, как взаимодействуют магниты.
Определить исходное положение полюсов.
Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.

Решение

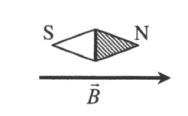
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Непосредственно над неподвижно закреплённой проволочной катушкой вдоль её оси на пружине подвешен полосовой магнит (см. рисунок). Куда начнёт двигаться магнит сразу после замыкания ключа? Ответ поясните, указав, какие физические явления и законы Вы использовали для объяснения.

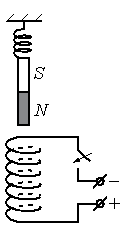
Алгоритм решения

Определить направление тока в соленоиде.
Определить полюса соленоида.
Установить, как будет взаимодействовать соленоид с магнитом.
Установить, как будет себя вести магнит после замыкания электрической цепи.

Решение

Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.

Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.

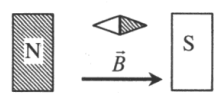
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).

pазбирался: Алиса Никитина | обсудить разбор | оценить