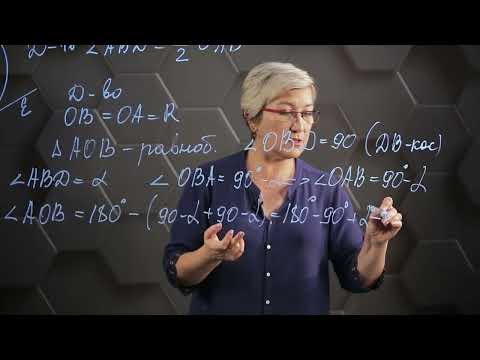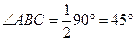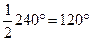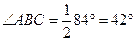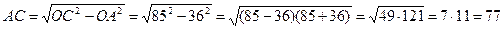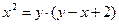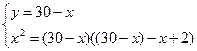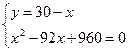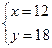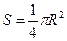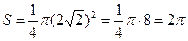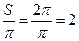Задание 6. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
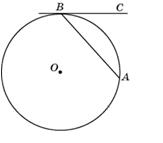
1-й способ. Сделаем построение – проведем радиус в точку B, а касательная с радиусом образовывают прямой угол (см. рисунок ниже).
В задании сказано, что градусная мера дуги AB равна 92°, следовательно, центральный угол AOB также равен 92°. Из равнобедренного треугольника AOB с AO=BO=r следует, что углы при основании равны:
.
Тогда угол ABC будет равен:
.
2-й способ. Угол между касательной и хордой равен половине дуги, заключённой между ними. Поэтому он равен 46.
Углы, связанные с окружностью
Угол, образованный двумя хордами, проведенными из одной точки, называется вписанным.
ТЕОРЕМА Вписанный угол измеряется половиной дуги, на которую он опирается.
все вписанные углы, опирающиеся на одну и ту же дугу, равны ;
вписанный угол, опирающийся на диаметр, прямой.
ТЕОРЕМА Угол, вершина которого лежит внутри круга, измеряется полусуммой двух дуг, заключенных между его сторонами
ТЕОРЕМА Угол, вершина которого лежит вне круга, а стороны пересекаются с окружностью, измеряется полуразностью двух дуг, заключенных между его сторонами.
ТЕОРЕМА Угол, составленный касательной и хордой, измеряется половиной дуги, заключенной внутри угла.
Задания с решением
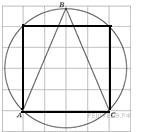
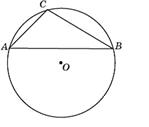
1. Найдите величину угла АВС. Ответ дайте в градусах.
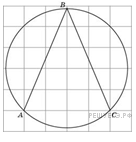
Решение.
Построим квадрат со стороной АС.
Тогда видно, что угол АВС опирается на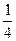 
окружности, то есть на дугу 90º. Вписанный угол равен половине дуги, на которую он опирается, значит 
2. Хорда АВ делит окружность на две части, градусные величины которых относятся как 6:12. Под каким углом видна эта хорда из точки С, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Решение.
Из точки C хорда АВ видна под углом АCВ. Пусть большая часть окружности равна 12х, тогда меньшая равна 6х. Вся окружность составляет 360º.
Получаем уравнение 12х+6х=360º.Откуда х=20º.
Угол АСВ опирается на большую дугу окружности, которая равна 12·20º=240º.
Вписанный угол равен половине дуги, на которую он опирается, значит, опирающийся на большую дугу угол АCВ равен 
3. Хорда АВ стягивает дугу окружности в 84º. Найдите угол АВС между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах.
Решение.
Угол АВС – это угол между касательной и хордой. Он измеряется половиной дуги, заключенной внутри угла. Дуга внутри угла равна 84º.Значит 
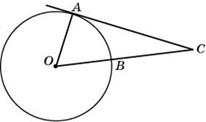
4. К окружности радиуса 36 проведена касательная из точки, удаленной от центра на расстояние, равное 85. Найдите длину касательной.
Пусть ОА=36, ОС=85.Радиус, проведённый в точку касания, перпендикулярен касательной. Из прямоугольного треугольника АОС по теореме Пифагора получаем 
5. К окружности из точки С вне ее проведены касательная АС и секущая СD, пересекающая окружность в точке В. Сумма длин касательной и секущей равна 30см , а внутренний отрезок секущей на 2см короче касательной. Найти длины касательной и секущей.
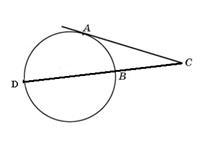
Пусть АС=х, а СD=у. Тогда х+у=30, а DB=AC-2=x-2 , BC=AC-DB=y-DB=y-(x-2)=y-x+2. По теореме, если из точки вне круга проведены к нему касательная и секущая, то квадрат касательной равен произведению секущей на ее внешнюю часть, то есть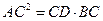 
. Тогда 
Получаем систему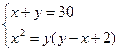 
. 
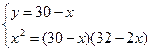
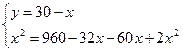
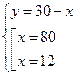
х=80 не подходит так как у>0 Поэтому получаем 
Касательная АС=12, секущая CD=18.
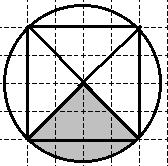
6. Найти площадь S закрашенного сектора. В ответе укажите S/π.
Построим на данном чертеже квадрат
Тогда становится очевидно, что сектор составляет одну четверть круга.
Радиус равен половине диагонали квадрата, сторона которого равна 4.
Тогда площадь сектора вычислим по формуле 
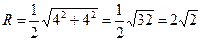
Тогда искомая величина равна 
Хорда AB стягивает дугу окружности в 92
27877. Хорда AB стягивает дугу окружности в 92 0 . Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
То есть другими словами хорде АВ соответствует центральный угол АОВ равный 92 0 :
*Отметим, что существует свойство – радиус и касательная, проведённые через общую точку образуют между собой угол 90 0 .
Для нахождения угла ABC нам нужно определить угол ОВА, так как 
Рассмотрим треугольник АОВ, он равнобедренный (АО и ОВ радиусы). В равнобедренном треугольнике углы при основании равны, значит