Градусные меры дуг окружности относятся как их длины (5 видео)

Градусные меры дуг окружности относятся как их длины

Найдите вписанный угол, опирающийся на дугу, длина которой равна длины окружности. Ответ дайте в градусах.

Градусные меры дуг окружности относятся как их длины, поэтому вписанный угол опирается на дугу

Вписанный угол равен половине дуги, на которую он опирается, тем самым, он равен 85°.

Содержание

Геометрия. Урок 5. Окружность
Определение окружности
Отрезки в окружности
Дуга в окружности
Углы в окружности
Длина окружности, длина дуги
Площадь круга и его частей
Теорема синусов
Примеры решений заданий из ОГЭ
5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
📽️ Видео

Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение окружности

Отрезки в окружности

Видео:ОГЭ 2021 Задание 16Скачать

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Видео:Длина дуги окружности. 9 класс.Скачать

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Видео:Геометрия Найдите градусные меры двух дуг окружности, на которые ее делят две точки, если градусныеСкачать

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

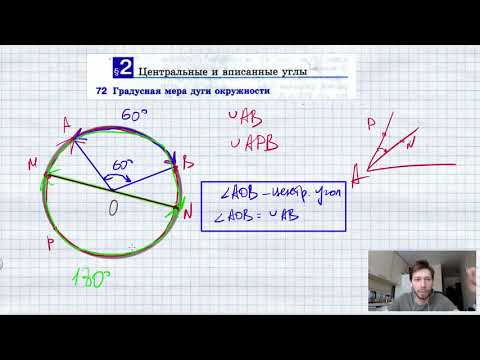
Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Видео:Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Видео:Градусная мера дуги окружности | Геометрия 7-9 класс #70 | ИнфоурокСкачать

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Видео:72. Градусная мера дуги окружностиСкачать

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Видео:ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Видео:Геометрия Найдите градусные меры двух дуг окружности, на которые ее делят две точки, если градуснаяСкачать

5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности

Видеоурок: Градусная мера дуги окружности

Лекция: Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности

Мерой угла называют величину, на которую отклоняется некоторый луч относительно первоначального положения.

Мера угла может измеряться двумя величинами: градусами и радианами, отсюда и название единиц – градусная и радианная мера угла.

Градусная мера угла

Градусная мера дает возможность оценить, какое количество градусов, минут или секунд помещается в тот или иной угол.

Расчет углов в градусах производится с точки зрения того, что полный поворот луча – это 360°. Половина поворота 180° — развернутый угол, четверть – 90° — прямой угол и т.д.

Радианная мера угла

А теперь давайте же разберемся, что такое радианная мера угла. Как известно из физики, существуют дополнительные единицы. Например, для измерения температуры основной единицей являются Кельвины, а дополнительной градусы Цельсия. Для измерения длины мы используем метры, а англичане используют футы. Данный список можно продолжать и далее. Смысл в том, чтобы Вы поняли, что, кроме градусной меры измерения угла, существует радианная мера, которая так же имеет право на существование.

Для определения радианной меры угла используют окружность. Считается, что радианная мера – это длина дуги окружности, описанная центральным углом.

Напомним, что центральный угол – это угол, вершина которого находится в центре окружности, а лучи опираются на некоторую дугу.

Итак, угол в 1 рад имеет градусную меру в 57,3°. Радианная мера угла описывается либо натуральными числами, или же с использованием числа π ≈ 3,14.

Для геометрии удобнее использовать градусную меру угла, однако для тригонометрии используют радианную меру.

Ниже представлена таблица, позволяющая переходить от градусов к радианам или же наоборот:

Если говорить о длине дуги, то длина дуги в 1 рад равна длине радиуса соответствующей окружности. То есть для определения длины дуги необходимо величину радиуса умножить на градусную меру дуги в радианах.