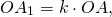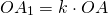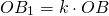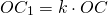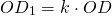homotecia представляет собой геометрическое изменение в плоскости, где расстояния от фиксированной точки, называемой центром (O), умножаются на общий коэффициент. Таким образом, каждая точка P соответствует другой точке P ‘, являющейся произведением преобразования, и они выровнены с точкой O.
Тогда гомотетия — это соответствие между двумя геометрическими фигурами, где преобразованные точки называются гомотетическими, и они выровнены с фиксированной точкой и сегментами, параллельными друг другу..
- 1 гомотеция
- 2 свойства
- 3 типа
- 3.1 Прямая гомотетия
- 3.2 Обратная гомотетия
- 4 Композиция
- 5 примеров
- 5.1 Первый пример
- 5.2 Второй пример
- 6 Ссылки
Видео:ГомотетияСкачать

homotecia
Гомотетия — это преобразование, которое не имеет конгруэнтного изображения, потому что из рисунка будет получена одна или несколько фигур большего или меньшего размера, чем исходная фигура; то есть гомотетия превращает многоугольник в другой подобный.
Чтобы гомотетия была выполнена, они должны соответствовать точка-точка и прямая-прямая, чтобы пары гомологичных точек были выровнены с третьей фиксированной точкой, которая является центром гомотетии..
Аналогично, пары линий, которые соединяют их, должны быть параллельными. Соотношение между такими сегментами является константой, называемой коэффициентом гомотетии (k); таким образом, что гомотетия может быть определена как:
Чтобы сделать этот тип преобразования, вы начинаете с выбора произвольной точки, которая будет центром гомотетии..
С этой точки отрезки линий рисуются для каждой вершины фигуры, которая должна быть преобразована. Масштаб, в котором выполняется воспроизведение нового рисунка, определяется по причине гомотетии (k)..
Видео:9 класс. Гомотетия. Построение треугольника. k=2Скачать

свойства
Одним из основных свойств гомотетии является то, что по причине гомотетии (k) все гомотетические фигуры схожи. Среди других выдающихся свойств являются следующие:
— Центр гомотетии (O) — единственная двойная точка, и она превращается в себя; то есть не меняется.
— Линии, проходящие через центр, трансформируются (они двойные), но точки, составляющие его, не являются двойными.
— Прямые, которые не проходят через центр, превращаются в параллельные линии; таким образом, углы гомотетии остаются неизменными.
— Образ сегмента с помощью гомотетии центра O и отношения k представляет собой отрезок, параллельный этому, и имеет k-кратную длину. Например, как видно на следующем изображении, сегмент AB с помощью гомотетики приведет к другому сегменту A’B ‘, так что AB будет параллельным A’B’, а k будет:
— Гомотетические углы конгруэнтны; то есть они имеют одинаковую меру. Следовательно, изображение угла — это угол, имеющий одинаковую амплитуду..
С другой стороны, гомотетия варьируется в зависимости от значения ее отношения (k), и могут возникнуть следующие случаи:
— Если константа k = 1, все точки фиксированы, потому что они трансформируются. Таким образом, гомотетическая фигура совпадает с оригиналом и преобразование будет называться тождественной функцией.
— Если k ≠ 1, единственной фиксированной точкой будет центр гомотетии (O).
— Если k = -1, гомотетия становится центральной симметрией (C); то есть вращение вокруг C будет происходить под углом 180 или .
— Если k> 1, размер преобразованного рисунка будет больше размера исходного.
— Да 0 0; то есть гомотетические точки находятся на одной стороне относительно центра:
Коэффициент пропорциональности или отношения сходства между прямыми гомотетическими фигурами всегда будет положительным.
Видео:9 класс. Геометрия. Гомотетия.Скачать

Гомотетия
Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу
где k — постоянное, отличное от нуля число, O — фиксированная точка.
Точка O называется центром гомотетии, число k — коэффициентом гомотетии.
гомотетия с коэффициентом k>0
Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:
и соединить вершины A1, B1, C1и D1 отрезками.
При k
и соединить вершины A1, B1, C1 отрезками.
При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.
При k= -1 гомотетия является симметрией относительно центра O (то есть центральная симметрия является частным случаем гомотетии).
Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.
Свойства преобразования гомотетии
1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.
2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).
Стороны гомотетичных фигур пропорциональны. а углы — равны.
Видео:Гомотетия. Коэффициент гомотетии. Центр гомотетии. Гомотетичные фигуры. Геометрия 8-9 классСкачать

Please wait.
Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

We are checking your browser. mathvox.ru
Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6dc65559be5a7b5b • Your IP : 85.95.188.35 • Performance & security by Cloudflare
📹 Видео
МЕРЗЛЯК-7 ГЕОМЕТРИЯ. КОНТРОЛЬНАЯ РАБОТА -2. ТРЕУГОЛЬНИКИСкачать

11.3 - Геометрия 7-9 класс ПогореловСкачать

8 класс, 23 урок, Второй признак подобия треугольниковСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

гомотетияСкачать

Геометрия, 10 класс | Преобразования плоскости. Гомотетия. Часть 2Скачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

урок №1 по геометрии по теме: Подобие фигур. ГомотетияСкачать

9 класс. Геометрия. Гомотетия. к=-1/2Скачать

Как проверяют учеников перед ЕНТСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Преобразование подобия. Гомотетия.Скачать

Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать