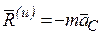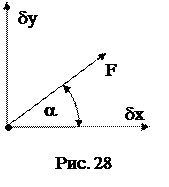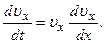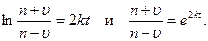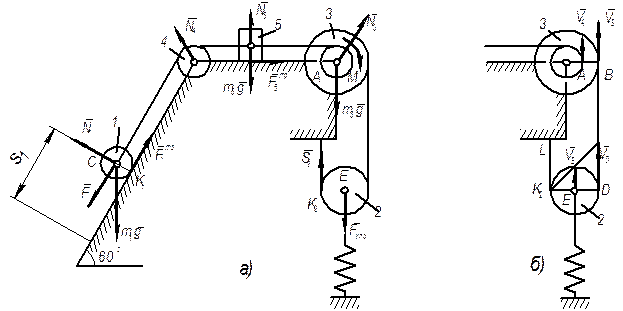Находить значения главного вектора и главного момента сил инерции непосредственно по формулам (22.6) затруднительно, так как в общем случае будем иметь дело с множеством сил инерции всех материальных точек системы. Поэтому целесообразно получить выражения главного вектора и главного момента сил инерции через параметры, характеризующие в целом механическую систему и ее движение.
Подставив в первое из равенств (22.7) значение ZT 7 / из теоремы о движении центра масс Мас = ЕГ/ (см. § 17.3), найдем
т. е. главный вектор сил инерции механической системы направлен противоположно вектору ас, а модуль его равен произведению массы системы на ускорение ее центра масс.
Подставив теперь во второе из равенств (22.7) значение ‘Lni0(Fk e ) из теоремы моментов (см. § 18.2) dK0/dt = Y.m0(F?), найдем
т. е. главный момент сил инерции механической системы относительно некоего центра О направлен противоположно вектору производной по времени от кинетического момента системы относительно того же центра.
Аналогичным будет соотношение для моментов относительно оси. Так, относительно оси z будет
Таким образом, все силы инерции механической системы можно эквивалентно заменить двумя векторами: силой Я ф , приложенной в произвольно выбранном центре О, и парой сил с моментом, равным М ф .
Рассмотрим, как эти величины определяются для твердого тела.
Если тело совершает поступательное движение, то ускорения всех его точек одинаковы и равны ускорению ас центра масс С
тела (ак =ас). Следовательно, все силы инерции —ткак образуют систему параллельных сил, которая приводится к равнодействующей Я ф = -Мас, линия действия которой будет проходить через точку С (здесь полная аналогия с силами тяжести). Сумма моментов сил инерции относительно точки С будет равна нулю.
Для твердого тела, вращающегося вокруг неподвижной оси Oz, величину главного момента сил инерции относительно этой оси определим, подставив в формулу (22.11) значение Kz = Jzсо (см. § 18.1):
т. е. модуль M°Z = Jzs, а направление момента противоположно
направлению углового ускорения е (это следует учитывать при выполнении чертежей для расчета).
Следовательно, система сил инерции такого вращающегося тела приводится к приложенной в точке О силе Я ф , определяемой формулой (22.8), и к паре, момент которой определяется формулой (22.12).
В частном случае, когда тело вращается вокруг оси Cz, проходящей через его центр масс С, получим R ф = 0, так как ас = 0, и система сил инерции приводится лишь к одной паре с моментом
ф , определяемой формулой (22.8) и приложенной в центре масс С тела, и паре сил с моментом = — /Сге (ось Cz перпендикулярна плоскости движения).
- Главный вектор и главный момент сил инерции
- Магия тензорной алгебры: Часть 14 — Нестандартное введение в динамику твердого тела
- Введение
- 1. Старый, как мир, принцип Даламбера
- 2. Принцип Даламбера для твердого тела. Главный вектор и главный момент сил инерции
- 3. На сцену выходят центр масс и тензор инерции
- 4. Особая роль центра масс
- Заключение
- 🔍 Видео
Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать

Главный вектор и главный момент сил инерции
Определение: главным вектором сил инерции называется вектор, равный геометрической сумме векторов сил инерции. 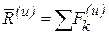
Просуммировав уравнения (51) с учетом того, что по свойствам внутренних сил (32) 
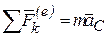
Определение: главным моментом сил инерции относительно точки О (оси), называется пара сил с моментом, равным геометрической сумме моментов сил инерции относительно той же точки (оси).
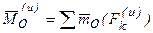
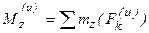
Поскольку система сил, определяемых уравнением (51) является уравновешенной, то для нее справедливо равенство:
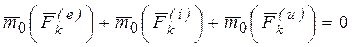
Просуммировав уравнения (52) с учетом того, что по свойствам внутренних сил (32) 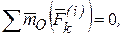
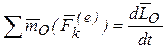
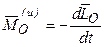
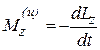
Приведение сил инерции для различных видов движения
В случае поступательного движения тела силы инерции, действующие на его точки, образуют систему параллельных сил, так как ускорения всех точек тела равны по величине и направлению, например, ускорению центра масс тела — 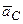
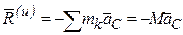
В случае вращательного движения тела, обладающего плоскостью материальной симметрии, вокруг оси, перпендикулярной этой плоскости и проходящей через центр масс тела, силы инерции могут быть приведены к паре сил с моментом, равным главному моменту сил инерции относительно оси вращения:
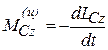
Учитывая, что: 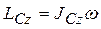
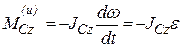
В случае когда ось вращения Oz не проходит через центр масс тела, силы инерции приводятся к силе 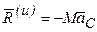
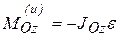
Приплоскомдвижении тела, имеющего плоскость симметрии и движущегося параллельно этой плоскости, силы инерции приводятся к силе, приложенной в центре масс тела и равной главному вектору сил инерции 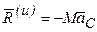
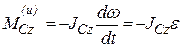
Принцип возможных перемещений
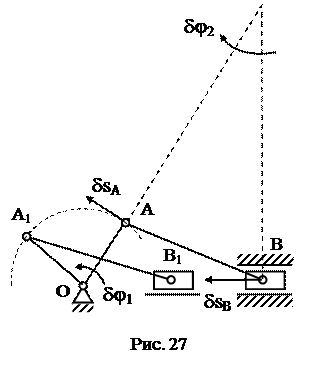
Определение: возможным называется бесконечно малое перемещение системы, которое допускают наложенные на нее связи. На рис. 27 показано возможное перемещение системы.
Направление возможных перемещений совпадает с направлением скоростей точек и угловых скоростей звеньев механизма. Перемещение из положения ОАВ в положение ОА1В1 не является возможным, так как оно конечное.
Определение: связь называется идеальной, если работа ее реакции на любом возможном перемещении равна нулю (например, гладкая поверхность).
Для равновесия системы с идеальными двухсторонними связями необходимо и достаточно, чтобы сумма работ активных сил, действующих на нее, на любом возможном перемещении равнялась нулю:
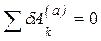
Общее уравнение динамики
Если к активным силам, действующим на систему с идеальными связями добавить силы инерции, то сумма работ этих сил на любом возможном перемещении будет равна нулю:
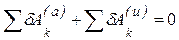
Общее уравнение динамики является суммой двух принципов: принципа Даламбера и принципа возможных перемещений. Действительно, если к неуравновешенной системе сил, действующей на механическую систему, добавить силы инерции, то согласно принципу Даламбера такая система сил будет уравновешенной и, следовательно, согласно принципу возможных перемещений
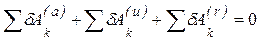
Но, поскольку связи, наложенные на систему, являются идеальными, то сумма работ их реакций на любом возможном перемещении равна нулю: 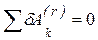
Уравнение Лагранжа II рода
Уравнение Лагранжа II рода имеет вид:
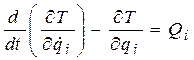
Здесь обозначено: T – кинетическая энергия системы; 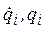
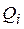
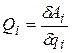
где 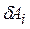
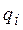
Например, для точки на рис. 28 обобщенные силы, соответствующие координатам x и y можно найти по формулам:
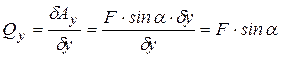
ЗАДАЧИ К КОНТРОЛЬНЫМ ЗАДАНИЯМ
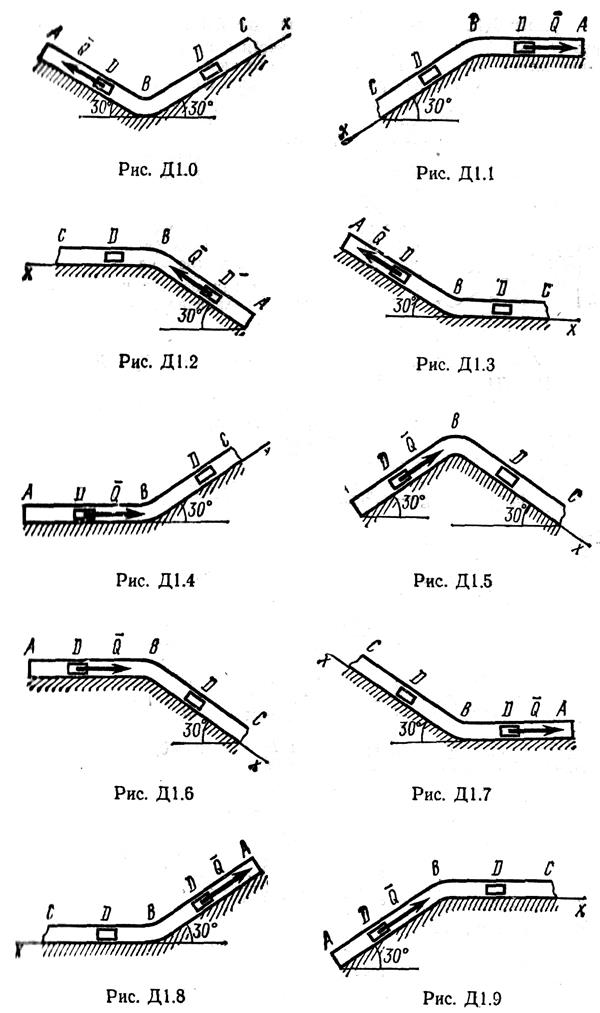
Задача Д1
Груз D массой m, получив в точке А начальную скорость υ0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ, на груз кроме силы тяжести, действуют постоянная сила 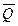
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него, кроме силы тяжести, действуют сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила 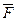
Указания.Задача Д1 – на интегрирование дифференциальных уравнений движения точки. (Решение основной задачи механики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке AB, учтя начальные условия. Затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая в этот момент t=0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти к переменной х, учтя, что:
| Номер условия | m, кг | υ0, м/с | Q, H | R, H | l,м | t, c | Fx, H |
| 0,4υ | — | 2,5 | 2sin(4t) | ||||
| 2,4 | 0,8 υ 2 | 1,5 | — | 6t | |||
| 4,5 | 0,5 υ | — | 3sin(2t) | ||||
| 0,6 υ 2 | — | -3cos(2t) | |||||
| 1,6 | 0,4 υ | — | 4cos(4t) | ||||
| 0,5 υ 2 | — | -6sin(2t) | |||||
| 1,8 | 0,3 υ | — | 9t 2 | ||||
| 0,8 υ 2 | 2,5 | — | -8cos(4t) | ||||
| 0,5 υ | — | 2cos(2t) | |||||
| 4,8 | 0,2 υ 2 | — | -6sin(4t) |
Пример Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой m действует сила тяжести и сила сопротивления 
Определить: x=f(t) – закон движения груза на участке ВС.
Решение.1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы 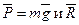
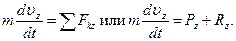
Далее находим Pz=P=mg, Rz=-R=-μυ 2 ; подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что υz=υ, получим
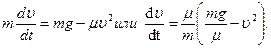
Введем для сокращения записей обозначение
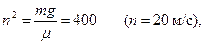
где при подсчете принято g≈ 10 м/с 2 . Тогда, разделяя в уравнении (2) переменные и взяв затем от обеих частей равенства интегралы, получим
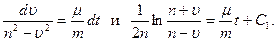
По начальным условиям при t = 0 υ=υ0=0, что дает С1=(1/2n)×ln1=0. Введя еще одно обозначение
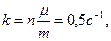
Отсюда находим, что
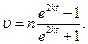
Полагая здесь t=t1=2 c и заменяя n и k их значениями (3) и (5), определим скорость υВ груза в точке В (число е=2,7):
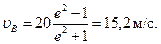
2. Рассмотрим движение груза на участке ВС; найденная скорость υВ будет для движения на этом участке начальной скоростью (υ0= υВ). Изображаем груз (в произвольном положении) и действующие на него силы 
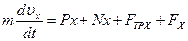
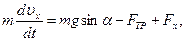
где FТР=fN. Для определения N составим уравнение в проекции на ось Вy. Так как ау=0, получим 0=N-mgcosα, откуда N=mgcosα. Следовательно, Fтр=fmgcosα; кроме того, Fx=16sin(4t) и управление (8) примет вид
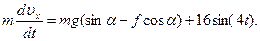
Разделив обе части равенства на m, вычислим
g(sinα – f cos α)=g(sin30˚-0,2cos30˚)=3,2; 16/m=2 и поставим эти значения в (9). Тогда получим
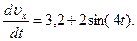
Умножая обе части уравнения (10) на dt и интегрируя, найдем
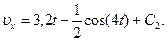
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t=0. Тогда при t=0 υ=υ0=υВ, где υВ дается равенством (7). Подставляя эти величины в (11), получим
При найденном значении С2 уравнение (11) дает
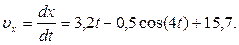
Умножая здесь обе части на dt и снова интегрируя, найдем
Так как при t=0 x=0, то C3=0 и окончательно искомый закон движения груза будет
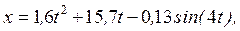
где x – в метрах, t – в секундах.
Задача Д4
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д4.0 – Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υ2, υс5 – скорости грузов 1, 2 и центра масс тела 5 соответственно, ω3 и ω4 – угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 1), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.
Указания. Задача Д4 – на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
| Номер условия | m1, кг | m2, кг | m3, кг | m4, кг | m5, кг | с, Н/м | М, Н×м | F=f(s), H | Найти |
| 1,2 | 80(4+5s) | ω3 | |||||||
| 0,8 | 50(8+3s) | υ1 | |||||||
| 1,4 | 60(6+5s) | υ2 | |||||||
| 1,8 | 80(5+6s) | ω4 | |||||||
| 1,2 | 40(9+4s) | υ1 | |||||||
| 1,6 | 50(7+8s) | υС5 | |||||||
| 0,8 | 40(8+9s) | ω3 | |||||||
| 1,5 | 60(8+5s) | υ2 | |||||||
| 1,4 | 50(9+2s) | ω4 | |||||||
| 1,6 | 80(6+7s) | υС5 |
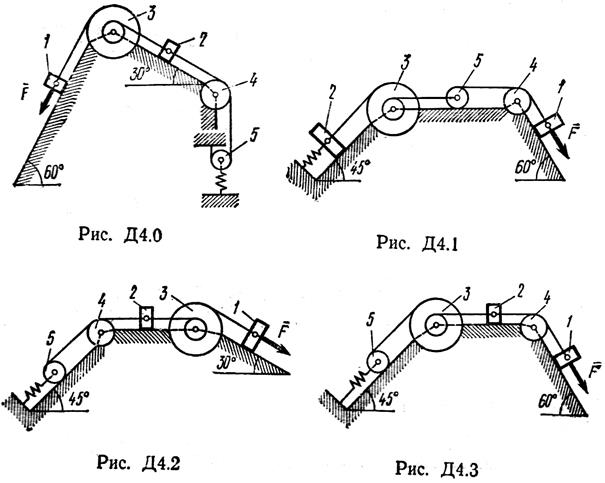
Пример Д4. Механическая система (рис. Д4, а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3 и радиусом инерции относительно оси вращения ρ3, блока 4 и груза 5(коэффициент трения груза о плоскость равен f). Тела системы соединены нитями, намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы F=f(s), зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.
Определить ω3 в тот момент времени, когда s=s1.
Решение.1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные 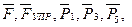
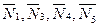
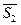
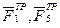
Для определения ω3 воспользуемся теоремой об изменении кинетической энергии:
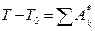
2. Определяем Т0 и Т. Так как в начальный момент система находилась в покое, то Т0=0. Величина Т равна сумме энергий всех тел системы:
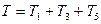
Учитывая, что тело 1 движется плоскопараллельно, тело 5 – поступательно, а тело 3 вращается вокруг неподвижной оси, получим
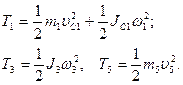
Все входящие сюда скорости надо выразить через искомую ω3. Для этого предварительно заметим, что υС1=υ5=υА, где А – любая точка обода радиуса r3 и что точка К1 – мгновенный центр скоростей катка 1, радиус которого обозначим r1. Тогда
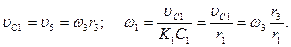
Кроме того, входящие в (3) моменты инерции имеют значения
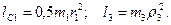
Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно
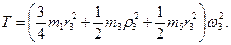
3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С1 пройдет путь s1. Введя обозначения: s5 – перемещение груза 5 (s5=s1), φ3 – угол поворота шкива 3, λ0 и λ1 – начальное и конечное удлинения пружины, получим
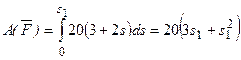
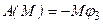
Работы остальных сил равны нулю, так как точки К1 и К2, где приложены силы 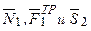
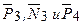
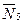
По условиям задачи λ0=0. Тогда λ1=sЕ, где sЕ – перемещение точки Е (конца пружины). Величины sE и φ3 надо выразить через заданное перемещение s1; для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, поскольку ω3=υА/r3=υC1 /r3 (равенство υС1=υА уже отмечалось), то и φ3=s1/r3.
Далее, из рисунка Д4, б видно, что υD=υB=ω3R3, а так как точка К2 является мгновенным центром скоростей для блока 2 (он как бы «катится по участку нити K2L), то υЕ=0,5υD=0,5ω3R3, следовательно, и λ1=sE=0,5φ3R3=0,5s1R3/r3. При найденных значениях φ3 и λ1 для суммы всех вычисленных работ получим
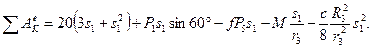
Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что Т0=0, придем к равенству
Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость ω3. Ответ: ω3=8,1с -1 .
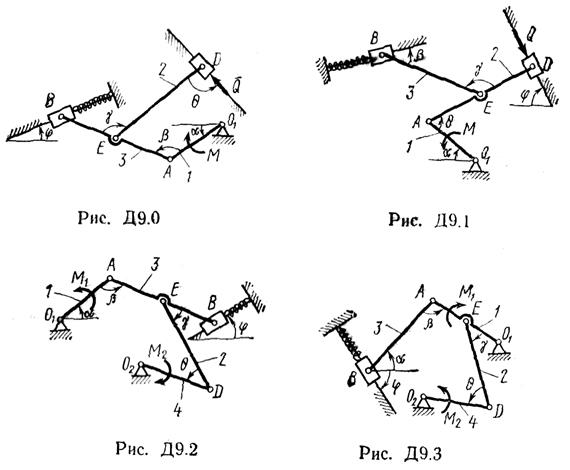
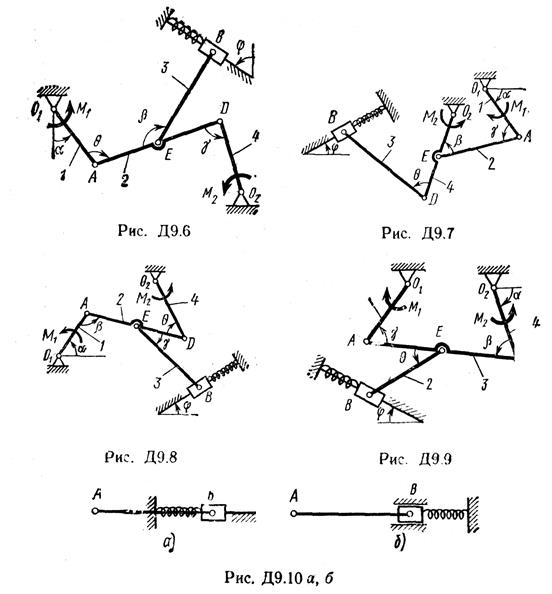
Задача Д9
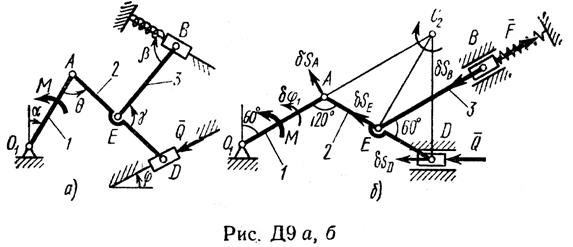
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами a, b, g, j, q (рис. Д9.0 – Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1 = 0,4 м, l4 = 0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины 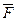
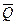
Определить, чему равна при равновесии деформация l пружины, и указать, растянута пружина или сжата. Значения всех заданных величин приведены в табл. Д9а для рис. Д9.0—Д9.4 и в табл. Д9б для рис. Д9.5—Д9.9, где Q выражено в ньютонах, а М, М1, М2 — в ньютон-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10б, где одновременно иначе изображены направляющие).
Указания. Задача Д9 — на определение условий равновесия механической системы с помощью принципа возможных перемещений. Механизм в рассматриваемой задаче имеет одну степень свободы, т. е. одно независимое возможное перемещение. Для решения задачи нужно сообщить механизму возможное перемещение, вычислить сумму элементарных работ всех действующих активных сил и пар на этом перемещении и приравнять ее к нулю. Все вошедшие в составленное уравнение возможные перемещения следует выразить через какое-нибудь одно.
Чтобы найти l, надо из полученного условия равновесия определить силу упругости F. На чертеже эту силу можно направить в любую сторону
(т. е. считать пружину или растянутой или сжатой); верно ли выбрано направление силы, укажет знак.
Таблица Д9а (к рис. Д9.0—Д9.4)
| Номер условия | Углы, град | с, Н/см | Для рис. 0—1 | Для рис.2 — 4 | ||||
| α | β | g | j | q | М, Н∙м | Q, Н | М1, Н∙м | M2, Н∙м |
Таблица Д9б (к рис. Д9.5—Д9.9)
| Номер условия | Углы, град | с, Н/см | М1, Н∙м | M2, Н∙м |
| α | β | g | j | q |
Пример Д9. Механизм (рис. Д9а), расположенный в горизонтальной плоскости, состоит из стержней 1, 2, 3 и ползунов B, D, соединенных друг с другом и с неподвижной опорой О1 шарнирами.
К ползуну В прикреплена пружина с коэффициентом жёсткости с, к ползуну D приложена сила 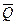
с= 125 Н/см, М = 150 Н×м, Q = 350 Н.
О п р е д е л и т ь: деформацию λ пружины при равновесии механизма.
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. Д9б); при этом согласно последнему из указаний к задаче Д9 прикрепляем пружину к ползуну с другой стороны (так, как если бы было β = 180°).
Для решения задачи воспользуемся принципом возможных перемещений, согласно которому
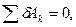
где δAk — элементарные работы активных сил на соответствующих возможных перемещениях.
Изображаем действующие на механизм активные силы: силу 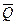
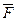
Неизвестную силу F найдем с помощью уравнения (1), а зная F и учитывая, что F = cλ, определим λ.
2. Чтобы составить уравнение (1), сообщим механизму возможное перемещение и введем следующие обозначения для перемещений звеньев, к которым приложены активные силы: δφ1 — поворот стержня 1 вокруг оси О1, δsD и δsB — перемещения ползунов (точек) D и В.
Из перемещений δφ1, δsD, δsB независимое от других — одно (у механизма одна степень свободы). Примем за независимое возможное перемещение δφ1 и установим, какими тогда будут δsD и δsB, выразив их через δφ1; при этом важно верно определить и направления δsD, δsB, так как иначе в уравнении (1) будут ошибки в знаках.
При расчетах учтем, что зависимость между возможными перемещениями здесь такая же, как между соответствующими скоростями звеньев механизма при его движении и воспользуемся известными из кинематики соотношениями (ход расчетов такой же, как в примере К3).
Сначала найдем и изобразим δsA (направление δsA определяется направлением δφ1); получим

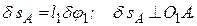
Теперь определим и изобразим δsD, учитывая, что проекции δsD и δsA на прямую АD должны быть равны друг другу (иметь одинаковые модули и знаки). Тогда
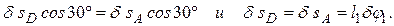
Чтобы определить δsB, найдем сначала δsE. Для этого построим мгновенный центр вращения (скоростей) С2 стержня 2 (на пересечении перпендикуляров к δsA и δsD, восстановленных из точек А и D) и покажем направление поворота стержня 2 вокруг С2, учтя направление δsA или δsD. Так как ÐС2АD = ÐC2DА = 60°, то DАС2D равносторонний и С2Е в нем высота, поскольку АЕ = ЕD. Тогда перемещение δsE, перпендикулярное С2Е, будет направлено по прямой ЕА (при изображении δsE учитываем направление поворота вокруг центра С2).
Воспользовавшись тем, что проекции δsE и δsA на прямую ЕА должны быть равны друг другу, получим (значение δsE можно найти и составив соответствующую пропорцию)
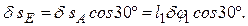
Наконец, из условия равенства проекций δsB и δsE на прямую ВЕ находим и изображаем δsB. Численно
3. Теперь составляем для механизма уравнение (1); получим
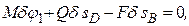
или, заменяя здесь δsD и δsB их значениями (3) и (5) и вынося одновременно δφ1 за скобки,
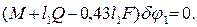
Так как δφ1¹0, то отсюда следует, что
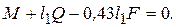
Из уравнения (8) находим значение F и определяем λ = F/с. Ответ: λ= 13,5 см. Знак указывает, что пружина, как и предполагалось, растянута.
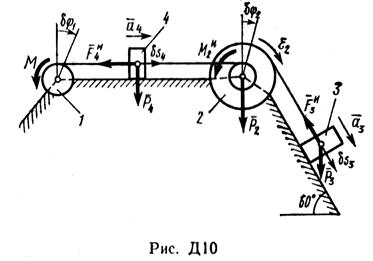
Задача Д10
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3—6, прикрепленных к этим нитям, и невесомого блока (рис. Д10.0—Д10.9, табл. Д10). Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны:
R1 = 0,2 м, r1 = 0,1 м, а шкива 2 — R2 = 0,3 м, r2 = 0,15 м; их радиусы инерции относительно осей вращения равны соответственно ρ1=0,1 м и ρ2=0,2 м. Пренебрегая трением, определить ускорение груза, имеющего больший вес; веса Р1, . Р6 шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2 изображать всегда как части системы).
Указания.Задача Д10 – на применение (к изучению движения системы) общего уравнения динамики (принципа Даламбера – Лагранжа). Ход решения задачи такой же, как в задаче Д9, только предварительно надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом М и = Jzε , где Jz – момент инерции тела относительно оси вращения, ε – угловое ускорение тела; направление М и противоположно направлению ε.
| Номер условия | P1 | P2 | P3 | P4 | P5 | P6 | M, H×м |
| 0,9 | |||||||
| 1,2 | |||||||
| 0,6 | |||||||
| 1,8 | |||||||
| 1,2 | |||||||
| 0,9 | |||||||
| 1,8 | |||||||
| 0,6 | |||||||
| 0,9 | |||||||
| 1,2 |
Видео:Момент инерцииСкачать

Магия тензорной алгебры: Часть 14 — Нестандартное введение в динамику твердого тела
Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Введение
Динамика твердого тела — раздел механики, который в своё время задал четкий вектор развития этой науки. Это один из самых сложных разделов динамики, и задача интегрирования уравнения сферического движения для произвольного случая распределения массы тела не решена до сих пор.
В этой статье мы начнем рассматривать динамику твердого тела, применяя аппарат тензорной алгебры. Эта пилотная статья о динамике ответит на ряд фундаментальных вопросов, касающихся, например, такого важного понятия как центр масс тела. Что такое центр масс, что отличает его от остальных точек тела, почему уравнения движения тела составляют в основном относительно этой точки? Ответ на эти, и некоторые другие вопросы находится под катом.
Интегрирование уравнений движения этой детской игрушки — одна из до сих пор не решенных задач механики.
Видео:момент инерции стержняСкачать

1. Старый, как мир, принцип Даламбера
Для начала рассмотрим движение материальной точки. Непосредственно из аксиом вытекает основное уравнение динамики точки
ускорение помноженное на массу есть векторная сумма приложенных к точке сил. И о силах, которые приложены к точке надо поговорить подробнее. В разделе механики, называемом аналитической механикой, силы, прикладываемые к точкам механической системе подлежат строгой классификации.
Силы, стоящие в правой части (1) разделяются на две группы
- Активные силы. Этой группе сил можно дать следующее определение
Активными называют силы, величину которых можно определить из условия задачи
Говоря формальным языком, активная сила определяется вектор функцией
где — обобщенная координата точки;
— обобщенная скорость точки. Из данного выражения видно, что начиная решать задачу о движении и имея начальные условия (момент времени, положение и скорость) можно сразу рассчитать активную силу.
Сила тяжести, упругости, Кулоновская сила взаимодействия заряда с электрическим полем, сила Ампера и сила Лоренца, сила вязкого трения и аэродинамического сопротивления — всё это примеры активных сил. Выражения для их расчета известны и эти силы можно посчитать, зная положение и скорость точки.
Реакции связей. Самые неприятные силы, которые только можно придумать. Напомню одну из аксиом статики, именуемую аксиомой о связях
Связи приложенные к телу можно отбросить, заменив их действие силой, или системой сил
Изображенная на рисунке точка — не свободная точка. Её движение ограничено связью, условно представленной в виде некой поверхности, в пределах которых располагается траектория движения. Приведенная выше аксиома дает возможность убрать поверхность, приложив к точке силу , действие которой эквивалентно наличию поверхности. При этом данная сила не является известной заранее — её величина удовлетворяет ограничениям на положение, скорость и ускорение, накладываемыми связью, ну и, разумеется вектор реакции зависит от приложенных активных сил. Реакции связей подлежат определению в процессе решения задачи. К реакциям связей относится так же и сухое трение, наличие которого даже в простой задаче существенно осложняет процесс её решения.
Исходя из данной классификации, уравнение движения точки (1) переписывают в виде
где — равнодействующая активных сил, приложенных к точке;
— равнодействующая реакций, наложенных на точку связей.
А теперь проделаем простейший фокус — ускорение с массой перенесем в другую часть уравнения (2)
и введем обозначение
Тогда, уравнение (2) превращается в
Сила, представляемая вектором (3) называется силой инерции Даламбера. А уравнение (4) выражает принцип Даламбера для материальной точки
Материальная точка находится в равновесии под действием приложенных к ней активных сил, реакций связей и сил инерции
Позвольте, о каком равновесии может идти речь, если точка движется с ускорением? Но ведь уравнение (4) есть уравнение равновесия, и приложив к точке силу (3) мы можем заменить движение точки её равновесием.
Достаточно распространен спор о том, являются ли силы инерции (3) физическими силами. В инженерной практике используется понятие центробежной силы, которая есть сила инерции, связанная с центростремительным (или осестремительным) ускорением, искривляющим траекторию точки. Моё личное мнение таково, что силы инерции есть математический фокус, продемонстрированный выше, позволяющий перейти к рассмотрению равновесия вместо движения с ускорением. Сила инерции (3) определяется ускорением точки, но оно, в свою очередь определяется действием на точку приложенных к ней сил, и в соответствии аксиоматикой Ньютона сила первична. Поэтому ни о какой «физичности» сил инерции говорить не приходится. Природа не знает активных сил, зависящих от ускорения.
Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

2. Принцип Даламбера для твердого тела. Главный вектор и главный момент сил инерции
Теперь распространим уравнение (4) на случай движения твердого тела. В механике его рассматривают как неизменяемую механическую систему, состоящую из множества точек, расстояние между которыми в каждый момент времени остается неизменным. Все точки тела движутся по различным траекториям, но уравнение движения каждой точки соответствует (2)
Силы, действующие на конкретную точку можно разделить на внешние активные , реакции внешних связей
, и внутренние силы
, представляющие собой силы взаимодействия рассматриваемой точки с остальными точками тела (по сути — внутренние реакции). Все упомянутые силы есть равнодействующие соответствующей группы сил, приложенных к точке. Применим к этому уравнению Принцип Даламбера
где — сила инерции, приложенная к данной точке тела.
Теперь, когда все точки тела находятся в равновесии, мы можем воспользоваться условием равновесия твердого тела, которое дает нам статика
Твердое тело находится в равновесии под действием приложенной к нему системы сил, если главный вектор и главный момент этой системы сил, относительно выбранного центра O, раны нулю
Главный вектор системы сил — это векторная сумма всех сил, приложенных к телу. Сумма сил, приложенных к каждой точке тела определяется последним уравнением, поэтому складывая уравнения для всех точек, в левой его части получим главный вектор
При этом, сумма внутренних сил равна нулю, как следствие из третьего закона Ньютона. Аналогично вычисляем сумму моментов всех сил относительно выбранного произвольного центра O, что дает нам равный нулю главный момент системы сил
причем, как показывается в классическом курсе динамики, сумма моментов внутренних сил, приложенных к системе материальных точек, равна нулю, то есть . Уравнения (5) и (6) уже выражают принцип Даламбера применительно к твердому телу, но лишь с одной необходимой поправкой.
Число активных сил и реакций связей в уравнениях (5) и (6) конечно. Большинство слагаемых в соответствующих суммах равны нулю, ибо активные внешние силы и реакции внешних связей, вообще говоря, приложены лишь в некоторых точках тела. Чего нельзя сказать о силах инерции — силы инерции приложены к каждой точке тела. То есть сумма сил инерции, и сумма их моментов относительно выбранного центра есть суммы интегральные. Систему сил инерции принято сводить к главному вектору и главному моменту и мы можем написать, что
главный вектор и главный момент сил инерции, приложенных к твердому телу. Интегралы (7) и (8) берутся по всему объему тела, а — радиус вектор точки тела относительно выбранного центра O.
Исходя из данного соображения мы можем переписать (5) и (6) в окончательном виде
Уравнения (10) и (11) выражают принцип Даламбера для твердого тела
Теврдое тело находится в равновесии под действием приложенных к нему внешних сил, реакций связей, главного вектора и главного момента сил инерции.
По сути (10) и (11) есть форма записи дифференциальных уравнений движения твердого тела. Они довольно часто применяются в инженерной практике, однако с точки зрения механики, такая форма записи уравнений движения не является самой удобной. Ведь интегралы (7) и (8) можно вычислить в общем виде и придти к более удобным уравнениям движения. В этой связи (10) и (11) следует рассматривать как теоретическую основу построения аналитической механики.
Видео:Разбор задачи на момент инерции стержняСкачать
3. На сцену выходят центр масс и тензор инерции
Вернемся к нашим тензорам и с их помощью вычислим интегралы (7) и (8) для общего случая движения твердого тела. В качестве центра приведения выберем точку O1. Эта точка выбрана в качестве полюса и в ней определен локальный базис связанной с телом системы координат. В одной из прошлых статей мы определили тензорное соотношение для ускорения точки тела в таком движении
Умножив (12) на массу точки со знаком минус, мы получим силу инерции, приложенную к элементу объема твердого тела
Выражение (13) — ковариантное представление вектора силы инерции. Двойное векторное произведение в (12) перепишем в более удобной форме, используя тензор Леви-Чивиты и псевдовекторы угловой скорости и углового ускорения
Подставляем (14) в (13) и берем тройной интеграл по всему объему тела, учитывая, что угловая скорость и угловое ускорение одинаковы в каждой точке этого объема, то есть их можно вынести за знак интеграла
Интеграл в первом слагаемом — это масса тела. Интеграл во втором слагаемом более интересная штука. Вспомним одну из формул курса теоретической механики:
где — контравариантные компоненты радиус-вектора центра масс рассматриваемого тела. Не в даваясь в смысл понятия центра масс просто заменим интегралы в (15) в соответствии с формулой (16), учтя, что во втором слагаемом (15) используются ковариантные компоненты.
Ага, выражение (17) тоже нам знакомо, представим его в более привычной векторной форме
Первое слагаемое в (18) — сила инерции, связанная с поступательным движением тела вместе с полюсом. Второе слагаемое — центробежная сила инерции, связанная с осествемительным ускорением центра масс тела при его движении вокруг полюса. Третье слагаемое — вращательная составляющая главного вектора сил инерции, связанная с вращательным ускорением центра масс вокруг полюса. В общем-то всё находится в соответствии с классическими соотношениями теормеха.
Пытливый читатель скажет: «зачем применять тензоры для получения этого выражения, если в векторном виде оно было бы получено не менее очевидным способом?». В ответ я скажу, что получение формул (17) и (18) — это была разминка. Теперь мы получим выражение главного момента сил инерции относительно выбранного полюса, и тут тензорный подход проявляет себя во всей красе.
Возьмем уравнение (13) и умножим его векторно слева на радиус вектор точки тела относительно полюса. Тем самым мы получим момент силы инерции, приложенной к элементарному объему тела
Снова выполним подстановку (14) в (19), но не станем торопится брать интеграл
Не знаю как у вас, а у меня рябит в глазах, даже при моей привычности к таким формулам. Слагаемые расположены в более естественном порядке — переставлены местами вращательная и центробежная составляющие. Кроме того, от первого слагаемого ко второму возрастает сложность преобразующих выкладок. Будем упрощать их по очереди, сначала упростим первое, сразу взяв интеграл
Тут снова появился радиус вектор центра масс. Здесь ничего сложного — ускорение полюса у нас одно и мы вынесли его за знак интеграла. Интерпретацией займемся чуть позже, а пока преобразуем второе слагаемое (20). В нем мы можем выполнить свертку произведения тензоров Леви-Чивиты по немому индексу k
Здесь мы воспользовались свойством дельты Кронекера заменять свободный индекс вектора/ковектора при выполнении свертки. Теперь возьмет интеграл, учтя, что угловое ускорение постоянно для всего объема тела
Во как! Малопонятный «крокодил», путем формальных тензорных преобразований схлопнулся в компактную формулу. Я лукавлю, мы ввели новое обозначение:
Но это не просто абстрактная формула. По структуре выражения (24) видно, что оно отражает распределение массы тела вокруг полюса и называется оно — тензор инерции твердого тела. Эта величина имеет поистине фундаментальное значение для механики, и о ней мы поговорим подробнее, пока лишь скажу, что (24) — тензор второго ранга, компонентами которого являются осевые и центробежные моменты инерции тела в выбранной системе координат. Он характеризует инертность твердого тела при вращении. Обращаю внимание читателя и на то, как быстро мы получили выражение для тензора инерции, по сути действуя формальным способом. С векторными соотношения без ломки мозгов не обойтись, в этом я убедился на личном опыте.
Ну и наконец обратимся к последнему слагаемому (20). При взятии интеграла в нём тоже должен получится тензор инерции, и мы будем преобразовывать его таким образом, чтобы достичь этой цели. В этой части выражения (20) должно фигурировать соотношение между тензором инерции и угловой скоростью тела. Приступим, для начало свернув произведение тензоров Леви-Чивиты
Налицо существенное упрощение выражения — за счет свойств дельты Кронекера и того, что векторное произведение . Но тензора инерции в (25) не видно. С целью его получить проведем ряд эквивалентных преобразований
Здесь мы снова учли, что , воспользовались свойствами дельты Кронекера и операцией поднятия/опускания индексов при умножении на метрический тензор. И, теперь мы интегрируем (26)
Здесь мы снова видим тензор инерции:
с учетом которого получаем компактное выражение для составляющей главного момента сил инерции, связанного с центробежными силами
Выражение (27) эквивалентно векторно-матричному соотношению:
И хоть меня и переполняют пафосные фразы, отложу их на потом, а сейчас аккуратно выпишу итоговый результат в векторной форме.
В общем случае движения твердого тела главный вектор и главный момент сил инерции, приложенных к твердому телу, равны
А теперь все же восхитимся — не смотря на то, что вышеприведенные преобразования похожи на египетские иероглифы, они формальны, мы просто выполняли действия над индексами тензоров и использовали свойства тензорных операций. Нам не надо было упражняться с векторами, расписывать векторные операции в компонентах и сводить получившиеся проекции векторов к результатам матричных операций. Все матричные и векторные операции конечных выражение вышли у нас автоматически. К тому же, естественным образом получены такие фундаментальные характеристики как координаты центра масс тела и тензор инерции.
Читая лекции студентам я задался целью вывести (29) и (30) оперируя векторами. После того как я перевел стопку бумаги и изрядно поломав мозги я пришел к результату. Поверьте на слово — вышеприведенные преобразования просто семечки, в сравнении с тем, через что надо пройти не используя тензоров.
К тому же, выражения (29) и (30) получены нами для произвольного центра приведения сил, в качестве которого мы взяли полюс O1. Эти выражения помогут нам понять что такое центр масс тела и его важность для механики.
Видео:Нахождение момента инерции стержня путем интегрированияСкачать

4. Особая роль центра масс
Используя формулы (29) и (30) вернемся к уравнениям (10) и (11) и, выполнив подстановку, придем к дифференциальным уравнениям движения твердого тела
Чем плохи эти уравнения? А тем, что они зависят друг от друга — ускорение полюса будет зависеть от углового ускорения и угловой скорости тела, угловое ускорение — от ускорения полюса. Вектор определяет положение центра масс тела по отношению к полюсу. А что если мы выберем полюс прямо в центре масс? Тогда ведь
и уравнения (31), (32) примут более простой вид
Узнаете эти уравнения? Уравнение (33) — теорема о движении центра масс механической системы, а (34) — динамическое уравнение Эйлера сферического движения. И эти уравнения независимы друг от друга. Таким образом, центр масс твердого тела — это точка, относительно которой силы инерции приводятся к наиболее простому виду. Поступательное движение вместе с полюсом и сферическое вокруг полюса — динамически развязаны. Тензор инерции тела, вычисляется относительно центра масс и называется центральным тензором инерции.
Уравнения (33), (34) в зарубежной литературе называют уравнениями Ньютона-Эйлера, и, в настоящее время весьма активно используются для построения ПО, предназначенного для моделирования механических систем. В рамках цикла о тензорах мы ещё не раз о них вспомним.
Видео:Расчет момента инерции стержняСкачать

Заключение
Прочитанная вами статья имеет две цели — в ней мы ввели базовые понятия динамики твердого тела и проиллюстрировали мощность тензорного подхода при упрощении громоздких векторных соотношений.
В дальнейшем мы подробнее остановимся на тензоре инерции и изучим его свойства. Погрузившись в дебри аналитической механики, сведем уравнения (31) — (34) к уравнениям движения в обобщенных координатах. В общем, рассказать ещё есть о чем. А пока, благодарю за внимание!
🔍 Видео
Урок 94. Вычисление моментов инерции телСкачать

момент инерции стержня относительно произвольной оси (неправильная задача)Скачать
Момент инерции абсолютно твердого тела. 10 класс.Скачать

Расчет момента инерции тонкого стержняСкачать

Что такое центробежная сила? Силы инерцииСкачать

5. Момент инерции простейших телСкачать

Зависимость углового ускорения от момента инерцииСкачать

Урок 97. Теорема ШтейнераСкачать

Момент импульса. 10 класс.Скачать

Найти момент инерции тонкого однородного стержня: Волькенштейн 3.5Скачать

13. Вычисление момента инерцииСкачать

Момент силы: почему его так назвали ?Скачать