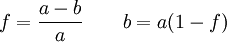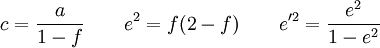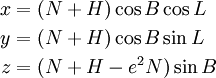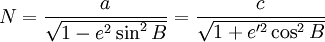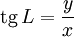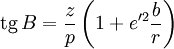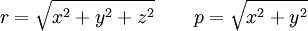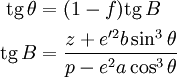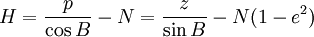Геоцентрический радиус вектор это

Географические информационные системы и дистанционное зондирование

Видео:Радиус-векторыСкачать

Геодезические системы пространственных координат

Рассматриваются преобразования между пространственными координатными системами. Приводится пример программной реализации на языке Питон.

Видео:Радиус векторСкачать

Содержание

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

[править] Земной эллипсоид

Земным эллипсоидом называется эллипсоид вращения, поверхность которого по форме и размерам довольно близка к поверхности геоида.

Поверхность эллипсоида образуется вращением эллипса вокруг его малой оси, которая также является осью вращения эллипсоида.

Эллипс обычно определяется размером его большой полуоси a и сжатием f. Реже вместо сжатия задаётся размер малой полуоси b:

В теории и практике вычислений широко используются такие параметры, как полярный радиус кривизны поверхности c, первый эксцентриситет e и второй эксцентриситет e′:

Пример функции Питона, вычисляющей по a и f параметры b, c, e и e′:

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

[править] Системы координат

Рассмотрим следующие системы координат.

1. Геоцентрические декартовы прямоугольные координаты:
   • начало координат находится в центре эллипсоида,
   • ось z расположена вдоль оси вращения эллипсоида и направлена в северный полюс,
   • ось x лежит в пересечении экватора и начального меридиана,
   • ось y лежит в пересечении экватора и меридиана с долготой L = 90°.
2. Система геодезических координат: геодезическая широта B угол между нормалью к поверхности эллипсоида и плоскостью экватора, геодезическая долгота L угол между плоскостями данного и начального меридианов, геодезическая высота H кратчайшее расстояние до поверхности эллипсоида.
3. Топоцентрические декартовы прямоугольные координаты:
   • начало координат находится в некоторой точке Q₀ (B₀, L₀, H₀) над эллипсоидом,
   • ось z расположена вдоль нормали к поверхности эллипсоида и направлена вверх,
   • ось x расположена в плоскости меридиана и направлена на север,
   • ось y перпендикулярна к осям x и z и направлена на восток.

Помимо широкого использования в геодезических целях, каждая из представленных координатных систем находит важное применение в прикладных областях.

Геодезические координаты со времён седой древности используются в навигации и картографии. В картографии они являются основой построения проекций.

Геоцентрическая система координат необходима для вычисления спутниковых орбит и решения других орбитальных задач.

Проекции, используемые картографами различных стран, основаны на различных геодезических датумах, т.е. созданы на различных эллипсоидах с разными размерами, положением центров и ориентацией осей в пространстве. Самый простой и точный способ пересчёта координат, заданных в разных датумах, зиждется на преобразованиях между геодезическими и геоцентрическими системами. В общем случае схема пересчёта координат между двумя проекциями выполняется в пять этапов:

1. координаты первой проекции — в геодезические координаты на первом эллипсоиде,
2. геодезические координаты — в геоцентрические координаты первого датума,
3. геоцентрические координаты первого датума — в геоцентрические координаты второго датума,
4. геоцентрические координаты — в геодезические координаты на втором эллипсоиде,
5. геодезические координаты — в координаты второй проекции.

Топоцентрическая система координат — естественная система для работы различных наземных объектов: ракетных стартовых комплексов, станций слежения за спутниками, станций ПВО и других измерительных комплексов. Естественно, собираемая информация в каждом случае преобразуется в общую систему координат, связанную с Землёй — геодезическую систему координат.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

[править] Преобразования координат

[править] Переход от геодезических координат к геоцентрическим

Это преобразование выполняется по следующим формулам:

Здесь N — так называемый радиус кривизны первого вертикала:

Реализация на Питоне:

[править] Переход от геоцентрических координат к геодезическим

Проще всего вычисляется долгота:

Сложнее с определением широты и высоты. Существует множество способов решения этой задачи. Воспользуемся итеративным методом Боуринга.

В начале находится предварительная оценка широты B:

Здесь r — геоцентрический радиус-вектор, p — расстояние от оси вращения эллипсоида:

Затем вычисляется параметр θ (приведённая широта) и получается уточнённое значение широты:

Действия по последним двум формулам предполагается повторять до сходимости к требуемой точности. Как правило, бывает достаточно одной итерации. В примере реализации метода Боуринга, приведённом ниже, запрограммировано две итерации.

В конце определяется высота:

[править] Переход от геоцентрических координат к топоцентрическим

Постановка задачи: начало топоцентрической системы координат задано точкой Q₀ (B₀, L₀, H₀); по геоцентрическим координатам точки Q (x, y, z) вычислить её топоцентрические координаты.

Конформное преобразование между двумя декартовыми прямоугольными системами координат всегда может быть представлено последовательностью сдвигов и вращений координатной системы. Данное преобразование можно реализовать по следующему алгоритму:

• сместить начало координат вдоль оси z на величину e² N₀ sin B₀ до вершины конуса, образованного нормалями, лежащими на параллели с широтой B₀,
• повернуть систему координат вокруг оси z на угол L₀, чтобы ось x оказалась в плоскости меридиана точки Q₀,
• повернуть систему координат вокруг оси y на угол 90° − B₀, чтобы ось z совпала с нормалью к поверхности эллипсоида в точке Q₀,
• сместить начало координат вдоль оси z на величину N₀ + H₀ в точку Q₀,
• изменить знак x на противоположный.

Функция toTopo() содержит обращения к функции вращения rotate():

[править] Переход от топоцентрических координат к геоцентрическим

Постановка задачи: начало топоцентрической системы координат задано точкой Q₀ (B₀, L₀, H₀); по топоцентрическим координатам точки Q (x, y, z) вычислить её геоцентрические координаты.

Алгоритм решения получается обращением алгоритма обратной задачи:

• изменить знак x на противоположный,
• сместить начало координат вдоль оси z на величину N₀ + H₀ в точку пересечения с осью вращения эллипсоида,
• повернуть систему координат вокруг оси y на угол B₀ − 90°, чтобы ось z совпала с осью вращения эллипсоида,
• повернуть систему координат вокруг оси z на угол −L₀, чтобы ось x оказалась в плоскости начального меридиана,
• сместить начало координат вдоль оси z на величину e² N₀ sin B₀ в центр эллипсоида.

[править] Переход от геодезических координат к топоцентрическим. Обратная пространственная задача

Постановка задачи: начало топоцентрической системы координат задано точкой Q₀ (B₀, L₀, H₀); по геодезическим координатам точки Q (B, L, H) вычислить её топоцентрические координаты x, y, z.

Задача решается последовательным применением готовых алгоритмов:

• по геодезическим координатам точки B, L, H вычислить её геоцентрические координаты x, y, z,
• по геоцентрическим координатам точки вычислить её топоцентрические координаты x, y, z.

Рассмотренная задача является разновидностью обратной геодезической задачи в пространстве. Вместо декартовых прямоугольных топоцентрических координат может требоваться вычисление каких-то других связанных с ними величин, например, полярных координат «дальность-азимут-зенитное расстояние», варианты могут быть разные. Однако в большинстве случаев сначала находятся топоцентрические x, y, z, по которым и выводятся искомые значения.

[править] Переход от топоцентрических координат к геодезическим. Прямая пространственная задача

Постановка задачи: начало топоцентрической системы координат задано точкой Q₀ (B₀, L₀, H₀); по топоцентрическим координатам точки Q (x, y, z) вычислить её геодезические координаты B, L, H.

Задача решается через вычисление геоцентрических координат:

• по тороцентрическим координатам точки x, y, z вычислить её геоцентрические координаты,
• по геоцентрическим координатам точки x, y, z вычислить её геодезические координаты B, L, H.

Эта задача является разновидностью прямой геодезической задачи в пространстве. Вместо декартовых прямоугольных топоцентрических координат могут задаваться какие-то другие связанные с ними величины, например, полярные координаты «дальность-азимут-зенитное расстояние», варианты могут быть разные. Однако в большинстве случаев сначала находятся топоцентрические x, y, z, по которым и решается задача.

Видео:ЕГЭ по Физике 2022. Кинематика. Радиус-векторСкачать

[править] Пример программной реализации

Коды вышеприведённых функций находятся в архиве Spheroid.zip в файле spheroid.py. Напишем программы, которые используют их для преобразования координат.

[править] Пересчёт топоцентрических координат в геодезические

В этом примере программы явно задаются параметры эллипсоида a, f и геодезические координаты начала топоцентрической системы B₀, L₀, H₀. Координаты точек x, y, z читаются из файла данных и пересчитанные значения B, L, H выводятся в консоль.

Этот скрипт находится в архиве Spheroid.zip в файле forwrd3d.py.

Файл данных должен содержать в каждой строке координаты одной точки x, y, z, разделённые пробелом. Создадим файл данных fwd3d.dat:

Выполним скрипт в командной строке:

Координаты на выходе:

Запишем полученные координаты в файл результатов inv3d.dat:

[править] Пересчёт геодезических координат в топоцентрические

В этом примере программы явно задаются параметры эллипсоида a, f и геодезические координаты начала топоцентрической системы B₀, L₀, H₀. Координаты точек B, L, H читаются из файла данных и пересчитанные значения x, y, z выводятся в консоль.

Этот скрипт находится в архиве Spheroid.zip в файле invers3d.py.

Файл данных должен содержать в каждой строке координаты одной точки B, L, H, разделённые пробелом. Используем в качестве файла данных созданный выше inv3d.dat:

Выполним скрипт в командной строке:

Координаты на выходе:

Видео:Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать

[править] Ссылки

Последнее обновление: 2017-03-07 09:34

Дата создания: 23.03.2014
Автор(ы): ErnieBoyd

Видео:10 Класс - Физика - Перемещение. Радиус-вектор.Скачать

Конспект лекций по курсу «Космическая геодезия и геодинамика» для студентов специальности 120103 (стр. 6 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Уравнение для лазерных измерений:

,

где t — временная задержка (время прохождения сигнала прямо и обратно), — поправка за приведение к центру масс спутника, — поправка за калибровку дальномера. Тропосферная задержка слабо зависит от погоды, поэтому метод считается абсолютным.

Для лазерной локации Луны используются уголковые рефлекторы, расположенные на советских космических аппаратах Луноход-1 и Луноход-2, а также доставленные во время лунных экспедиций американских кораблей Аполлон-11, -14 и -15 [ Bur š a , Kosteleck ý 1999].

Радарные системы не зависят от погоды; используемые длины волн сантиметрового и дециметрового диапазона. Время распространения значительно зависит от влияния рефракции радио волн в атмосфере.

Различают однонаправленный и двунаправленный способы измерений расстояний.

Рис. 12. Схема работы лазерного дальномера (двухпутный метод)

Рис. 13. Лазерный спутниковый дальномер

Система контроля наведения Измерение времени t Регистрация данных Уголковые отражатели Следящий телескоп и детектор Лазер

3.5.3. Доплеровские наблюдения. Измерение разностей расстояний

Другой принцип позиционирования, используемый в радионавигации, основан на эффекте Доплера, при котором происходит изменение частоты сигнала, принятого наблюдателем, из-за относительного движения передатчика и приемника. Доплеровский сдвиг частоты определяется как разность между частотой принятого сигнала и частотой радио источника. Переданная и принятая частоты, fT и fR , связаны соотношением:

, (2.10)

где r – изменяющееся расстояние между передатчиком и приемником, — скорость изменения этого расстояния или лучевая скорость, vs – скорость распространения сигнала. Вместо термина «лучевая скорость» может применяться термин «радиальная скорость».

Доплеровскому сдвигу частоты fD = fT – fR соответствуют поверхности положения в виде конусов. Вершины конусов совпадают с положениями спутника ( S 1, S 2, S 3 на рис. 14), осями конусов являются векторы полной скорости V 1, V 2, V 3. Угол раствора конуса равен углу между векторами полной и лучевой скорости.

Рис. 14. Позиционирование по лучевой скорости.

3.5.4. Спутниковая альтиметрия

Это особая форма измерения расстояний, где измеряется вертикальное расстояние между спутником и поверхностью океана. Спутниковая альтиметрия была действительно первым способом измерений спутник-земля. Спутник имеет на борту радарный альтиметр, никаких базовых станций на земле не требуется. Высота альтиметра над поверхностью моря a 0 измеряется по времени двустороннего прохождения сигнала, который излучается спутником и отражается от морской поверхности.

Если высота орбиты спутника над эллипсоидом h известна, и обеспечивает приближенное соотношение

То есть среднее расстояние между уровнем моря и эллипсоидом (рис. 4.8) .Следовательно, спутниковую альтиметрию можно использовать для определения геоида на океанах.

Спутники GEOS -3 и SEASAT -1 были первыми двумя спутниками, которые несли радарные альтиметры, и интенсивно использовались для геодезических целей. Другими спутниками были GEOSAT , ERS -1, ERS -2, TOPEX — POSEIDON , GFO , JASON , ENVISAT , обеспечившими значительный вклад в геодезию, геофизику и океанографию. Запуск дополнительных спутников, оборудованных радио альтиметрами, ожидается в ближайшие несколько лет. Спутниковая альтиметрия с лазерной системой в стадии подготовки. Первый лазерный альтиметр был запущен на спутники ICESAT .

3.5.6 Системы спутник-спутник. Гравитационные миссии

Модель гравитационного поля должна иметь тот же уровень точности, что и обычно достигается для глобального определения положения. Некоторые из вкладов в различные области геодезии будут ( Schuyer , 1997) будут:

Геодезия – глобальная система высот, определение высот через GPS , движения льда и вертикальные движения земной поверхности,

Геофизика – процессы в земной коре и мантии, континентальной литосфере (пост-ледниковая отдача), океаническая литосфера (процессы субдукции),

Океанография – абсолютные циркуляции, изменение уровня моря, изменения климата.

Единственная прогнозируемая возможность для удовлетворения этих требований связана с гравитационными полевыми миссиями с высоким разрешением. Их сущность заключается в использовании спутников как гравитационные зонды в поле силы тяжести Земли. Чтобы преодолеть ограничения, связанные с наземными наблюдениями спутников, представляющими традиционные методы, должны выполняться три фундаментальных критерия:

— высота орбиты как можно ниже (200-500 км),

— непрерывный охват трехмерными наблюдениями больших орбитальных дуг, и

— разделение гравитационных и негравитационных сил, действующих на спутник.

С такими соображениями реализуются две концепции, которые уже проверены (см. также Rummel et al ., 2002). Это:

— наблюдения спутник-спутник (измерения расстояний и скорости изменения расстояний между спутниками), и

— спутниковая градиентометрия (измерение разности ускорений силы тяжести внутри спутника.

По первой концепции различают конфигурации между высокий-низкий и низкий-низкий. На рис. 15 продемонстрированы все три метода.

Рис. 15. Разные концепции, посвященные гравитационным полевым миссиям: SST — HL , SST — LL , SGG по [ Rummel et al ., 2002]

Наблюдения спутник-спутник в режиме высокий-низкий ( SST — HL ) означают, что спутник на орбите LEO наблюдается высокими спутниками типа GPS , ГЛОНАСС или Galileo относительно сети наземных станций. Негравитационные силы, действующие на низкий спутник, измеряются акселерометрами. Спутник LEO является зондом в гравитационном поле Земли, который можно точно и непрерывно наблюдать. Наблюдаемые 3- D ускорения соответствуют гравитационным ускорениям.

Наблюдения спутник-спутник в режиме низкий-низкий ( SST — LL ) означают, что два спутника LEO находятся на одной и той же низкой орбите, разделенные несколькими сотнями километров, и что расстояние D между обоими спутниками измеряется по межспутниковой линии связи с максимально возможной точностью. Снова, влияние негравитационных сил, действующих на два спутника LEO , можно либо измерить, либо компенсировать (см. [4.3.3.1]). В сущности, разность ускорений между двумя LEO измеряется. Конфигурация LL может объединяться с конфигурацией HL . Одно преимущество над чистым методом HL состоит в том, что вычитание (образование разностей) наблюдений обеспечивает намного более высокую чувствительность.

Спутниковая градиентометрия ( SSG ) означает, что измеряется разность ускорений непосредственно на спутнике. Поскольку КА находится в свободном падении, то ускорения можно измерить от центра масс спутника идеально во всех трех направлениях. Одно важно преимущество по сравнению с методом SST состоит в том, что негравитационные ускорения оказываются одинаковыми для всех измерений внутри КА, и, следовательно, исключаются при вычитании.

В первом случае ( SST — HL ) измеряются первые производные от гравитационного потенциала, а во втором случае ( SST — LL ) – разности первых производных вдоль длинной базовой линии. В третьем случае ( SSG ) определяются вторые производные. Кратко, методы можно охарактеризовать как

SST — HL – измерение ускорений на одном LEO ,

SST — LL измерение разностей ускорений между двумя LEO ,

SSG — измерения in situ градиентов ускорений в пределах одного LEO .

Было разработано огромное количество предложений по всем трем концепциям в течение последних 30 лет. Среди них – Geopotential Research Mission (GRM), Aristoteles или STEP (Satellite Test of the Equivalence Principle). Их обзор см. в Sneeuw , Ilk 1997. Хотя эти проекты не были реализованы, принципы, разработанные в них, тем не менее, вошли в большинство существующих или планируемых космических экспериментов.

Замечательно, что все три упомянутых выше метода возможно будут реализованы в первое десятилетие нового столетия в миссиях CHAMP , GRACE и GOCE . Этому периоду поэтому дано название – Десятилетие геопотенциальных исследований – Decade of Geopotentional Research . Эти миссии имеют различные характеристики и, следовательно, удовлетворяют разным аспектам определения высокоточного точного гравитационного поля. Рис. 10.1 дает представление об этом. Все три миссии будут значительно улучшать наилучшую существующую модель гравитационного поля EGM -96 на несколько порядков величин: CHAMP – до 70 порядок и степени, GRACE – примерно до 140, GOCE – до 350 порядка и степени. В то время как GRACE показывает наивысшую точность для низких гармоник до 70 порядка и, следовательно, может выявлять изменения гравитационного поля во времени на этом уровне, GOCE показывает наилучшие результаты между степенями 70 и 350 и может также обеспечить геоид с точностью 1 см для коротких полуволн с длиной около 80 км. Больше деталей дается в следующих двух разделах и в цитируемой литературе.

КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ «КОСМИЧЕСКАЯ ГЕОДЕЗИЯ И ГЕОДИНАМИКА» ДЛЯ СТУДЕНТОВ СПЕЦИАЛЬНОСТИ 300500

4.1 ОСНОВНОЕ УРАВНЕНИЕ КОСМИЧЕСКОЙ ГЕОДЕЗИИ

Космическая геодезия занимается решением задач геодезии (определение формы и размеров Земли и ее гравитационного поля) посредством наблюдений различных искусственных и естественных небесных тел. Среди таких небесных тел наибольший интерес в последние годы представляют квазары из-за их точечных размеров и отсутствия собственного движения и геодезические (в том числе навигационные) ИСЗ. На спутниках можно устанавливать специальное оборудование, которое позволяет решать задачи геодезии наиболее эффективным образом.

Введем в рассмотрение геоцентрическую земную систему отсчета OXYZ (рис. 1). Обозначим через R и r геоцентрические радиус векторы соответственно для пункта и спутника, r – топоцентрический радиус вектор спутника. Очевидное векторное соотношение

(1)

позволяет решать весь комплекс задач космической геодезии, почему его иногда называют основным уравнением космической геодезии. Предполагается, что компоненты вектора r получаются из наблюдений, а из векторов R и r один может быть известным, а другой — определяемым.

Рис. 1. Основная концепция позиционирования точки по спутнику

R –геоцентрический вектор положения антенны приемника,

r — геоцентрический вектор положения спутника,

ρ – топоцентрический вектор положения спутника относительно антенны.

Если известен вектор положения пункта наблюдений R , то можно найти координаты спутника:

. (2)

В таком виде основное уравнение используется для решения прямых задач космической геодезии. По нескольким положениям одного и того же спутника можно определить его орбиту. Если известно положение спутника на орбите r и измерен топоцентрический вектор r , то можно найти положение пункта наблюдений:

. (3)

Это выражение используется для решения обратных задач космической геодезии.

Построение любой геодезической сети, когда координаты от одних пунктов передаются на другие пункты, состоит в объединении прямых и обратных геодезических задач. Построение спутниковых геодезических сетей сводится к объединению прямых и обратных задач космической геодезии с использованием ИСЗ геометрическим или динамическим методом. В геометрическом методе обеспечивается синхронность наблюдений одного и того же спутника как минимум с двух пунктов с координатами R 1 и R 2, и передача координат происходит по схеме:

. (4)

Из этого уравнения видно, что

, (5)

т. е. геометрический метод по своей природе является относительным, и координаты спутника в передаче координат пунктов непосредственно не участвуют. Поэтому считается, что в геометрическом методе для получения положения спутника на орбите не требуется применять теорию его движения, а сам спутник используется только как высокая визирная цель или передатчик радиосигналов.

Вектор D 12, выражающий приращение координат между пунктами, при построении сетей космической триангуляции было принято называть «хордовым вектором». В современных спутниковых технологиях его обычно называют «вектором базовой линии». Очевидно, что

. (6)

Если построена сеть из хордовых векторов, включающая N пунктов, то положение i можно найти как

(7)

В динамическом методе синхронность наблюдений не является важным обстоятельством, более того, преимущественно используются несинхронные измерения, а объединение всех наблюдений производится под условием их принадлежности одной и той же мерной дуге. Поскольку передача координат производится через орбиты спутников, требуется совершенная теория их движения. В динамическом методе определяются не только координаты пунктов наблюдений, но также параметры орбит, геофизические параметры, входящие в характеристики возмущающих сил, действующих на спутники, в частности, параметры гравитационного поля Земли. Разновидностью динамического метода является орбитальный метод космической геодезии. В орбитальном методе модель гравитационного поля Земли предполагается хорошо известной, а из геофизических параметров могут определяться лишь те, которые сравнительно быстро изменяются, как, например, плотность атмосферы.

В орбитальном методе разработано несколько вариантов его реализации. Наиболее общая схема орбитального метода, когда производится уравнивание всех выполненных наблюдений с определением координат пунктов, орбит и геофизических параметров применяется, например, в центрах обработки Международной геодинамической службы. Повседневным стало применение навигационного варианта орбитального метода. В этом методе вначале по наблюдениям с опорных пунктов определяется орбиты спутников, далее они экстраполируются на некоторое время вперед и засылаются на спутники, а когда производятся измерения с неизвестных пунктов, параметры движения навигационных спутников передаются с них наблюдателю [Баранов и др. 1986].

4.2 АБСОЛЮТНОЕ И ОТНОСИТЕЛЬНОЕ ПОЗИЦИОНИРОВАНИЕ

Под позиционированием понимается определение пространственного положения объектов:

— по отношению к системе координат, начало которой однозначно определено и в общем случае недоступно. Определение положения в этой системе известно как позиционирование точки или абсолютное позиционирование.

— по отношению к другой точке, принимаемой за начало некоторой местной системы координат. Этот способ позиционирования известен как относительное позиционирование или дифференциальное позиционирование.

4.2.1 Абсолютное позиционирование

При абсолютном позиционировании должна быть строго определена и поддерживаться система отсчета (система опорных координат). Никакой прямой доступ к началу или опорным осям обычно невозможен и вся надежда ложится на совокупность опорных точек, несущих координатную систему. Обычно начало находится в центре масс Земли (геоцентре), а оси системы определяются общепринятым способом. В классической геодезии единственным средством, которым можно было определить абсолютное положение (точнее, плановые компоненты положения) были астрономические наблюдения.

В современной геодезии спутниковые наблюдения предлагают средство, которым можно определять трехмерное положение с различными степенями точности. Спутниковое позиционирование точки является процессом, в котором:

(1) дается вектор положения наблюдаемого спутника (в общеземной системе);

(2) дается топоцентрический вектор от наземной станции наблюдений до наблюдаемого спутника (в той же самой системе);

(3) определяется вектор положения наземной станции.

Концептуально это проиллюстрировано на рис. 1. К нему можно сделать следующие замечания:

— в зависимости от того, как измеряется вектор расстояния, возможны различные методы позиционирования,

— вектор положения спутника изменяется во времени, и требуется решать задачу вычисления спутниковых эфемерид, что требует применения алгоритмов небесной механики,

— наземная наблюдательная станция может быть стационарной, но может и находиться в движении,

— «естественной» системой координат для спутникового позиционирования является геоцентрическая система координат, обычно реализуемая в форме прямоугольных или геодезических координат. Главная ось этой системы направлена по оси вращения Земли, а основные направления выбираются в зависимости от решаемой задачи (либо в точку пространства, если система не вращается, либо в точку пересечения меридиана Гринвича и плоскости экватора для системы жестко связанной с Землей).

В некоторых методах космической геодезии положение стационарного объекта можно определять очень точно, например, в методе лазерной локации спутников. Однако обычно координаты пункта в абсолютном смысле определяются со значительно меньшей точностью, чем точность самих измерений.

4.2.2 Относительное позиционирование

Относительное позиционирование применяется и в обычной наземной геодезии, и в космической геодезии. Хотя координаты выражаются через три компоненты глобальной системы отсчета, они выводятся из наблюдений, сделанных вблизи контрольных точек, координаты которых известны.

В классической геодезии абсолютные координаты «начальной» станции в геодезической системе назначаются произвольным образом, а их связь с геоцентром поэтому определена с малой точностью. Однако в результате высокоточных геодезических измерений координаты других станций определяются со сравнительно высокой точностью, но только в относительном смысле. Таким способом может быть определен полный набор точек и образована сеть. Эта сеть является эффективным средством для распространения координат, и, имея много возможных «путей» передачи координат от одной станции к другой, можно использовать «избыточную» информацию для «уравнивания» сети, чтобы вывести наилучший набор координат для всех точек.

Поскольку методы обычного наземного позиционирования в прошлом использовались исключительно для определения векторов между станциями, связи между отдельными пунктами сети были ограничены взаимной видимостью. Принято различать плановые геодезические сети, в которых определяются широты и долготы опорных точек, и геодезические нивелирные сети, в которых точно определяются высоты. Обычно точки плановых сетей имеют слабо определенные высоты, а нивелирные реперы, как правило, не имеют плановых координат.

В случае СРНС абсолютное положение чаще всего определяется с невысокой точностью (то есть координаты относительно геоцентра известны довольно грубо), но относительные положения любой пары пунктов определяются с высокой точностью. Концептуально, относительное положение равно разности координат двух пунктов (в общеземной системе), выраженной в локальной системе отсчета с началом в одной из точек сети. Большая часть ошибок в абсолютных положениях являются общей для всех координат, и, следовательно, исключаются в компонентах базовых линий. В этом случае точность позиционирования приближается к точности измерения самих измерений, и поэтому является стандартным методом спутниковых измерений (а также точной навигации).

(8)

Геоцентрический радиус-вектор спутника r i является функцией текущих элементов орбиты , где j – номер мерной дуги (номер орбиты), ti – эпоха наблюдений спутника i . Поскольку , то

(9)

В свою очередь элементы орбиты на текущую эпоху являются функциями от вектора начальных условий движения НУД , поэтому можно записать:

. (10)

В этом уравнении

— матрица частных производных от параметров наблюдений по небесным геоцентрическим координатам спутника;

(11)

(12)

— матрица изохронных производных.

Матрица производных от параметров наблюдений по координатам пункта:

(13)

Вместо представления в Кеплеровых элементах орбиты может использоваться представление в других элементах (например, регулярных) или в прямоугольных координатах. В этом случае вектор НУД задается как =. Тогда матрица изохронных производных выглядит следующим образом:

(14)

В динамическом методе в уравнение поправок добавляются неизвестные гармонические коэффициента геопотенциала Cnm , Snm или поправки к известным гармоническим коэффициентам:

, (15)

где , и .

КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ «КОСМИЧЕСКАЯ ГЕОДЕЗИЯ И ГЕОДИНАМИКА» ДЛЯ СТУДЕНТОВ СПЕЦИАЛЬНОСТИ 300500

5. ГЛОБАЛЬНЫЕ РАДИО НАВИГАЦИОННЫЕ СПУТНИКОВЫЕ СИСТЕМЫ

Приведем некоторые характеристики о спутниковых системах позиционирования, прошлых, действующих и планируемых.

5.1 Доплеровская система TRANSIT

История TRANSIT начинается со старта космических запусков (4 октября 1957 года). Когда в СССР был запущен Первый спутник, то доплеровское смещение сигналов было использовано для определения орбиты спутника. Впоследствии метод был реализован в обратном порядке таким образом, что, если орбита была известна, то положение приемника можно было определить [ Misra and Eng 2001]. Навигационные системы первого поколения, построенные на базе низкоорбитальных спутников, разрабатывались и вводились в строй в 60–70 гг. В США была разработана система навигации для ВМС под названием NNSS (Navy Navigation Satellite System), впоследствии получила наименование TRANSIT. В ее состав входили спутники типа Oscar и Nova .

Рис. 1. Конфигурация доплеровской спутниковой системы позиционирования TRANSIT (пять спутников на полярных орбитах).

Разработка системы TRANSIT началась в 1959 г., первый спутник был запущен в 1961 г. Система стала пригодна для военного использования с 1964 г. и была реализована для гражданского использования с 1967 г. Спутники ведут передачи на двух частотах (400 и 150 МГц), с фазовой модуляцией навигационных сообщений. Система в рабочем состоянии имеет небольшое количество спутников (4-6) на полярных орбитах с высотой около 1075 км и периодом обращения 107 минут (рис. 1.18), что подразумевает непродолжительное время прохождения в зоне видимости пункта (обычно в пределах 15 минут). Точность вычисления координат источника в системах первого поколения в большой степени зависит от погрешности определения скорости источника. Так, если скорость объекта определена с погрешностью 0,5 м, то это в свою очередь приведёт к ошибке определения координат в 500 м. Для неподвижного объекта эта величина уменьшается до 50 м. Для геодезического использования этой системы были разработаны малогабаритные приемники GEOCEIVER, позволяющие определять координаты с субметровой точностью. С помощью этой системы, в частности, в СССР и затем в России в 1984–1993 гг. была создана доплеровская геодезическая сеть.

Система в ышла из применения в 1996 г.

5.2 Доплеровская система Цикада

Разработки системы ЦИКАДА (другое название «Надежда») начались в СССР в 1963 г. В 1967 г. на орбиту был выведен первый отечественный навигационный спутник «Космос-192».

С РНС « Цикада-М » — это низкоорбитальная, глобальная, доплеровская система, предназначенная для навигационного обеспечения военных морских потребителей ВМС России. С 1990 г. система открыта для использования гражданскими потребителями. Система ограниченно применяется в целях топогеодезической привязки объектов. Прекращение работы системы «Цикада-М» в 1997 г.

Состав системы «Цикада-М» — 6 космических аппаратов (КА), находящихся на круговых орбитах на высоте 1000 км с углом наклонения 83°.
Оборудование наземных средств контроля и управления выработало технический ресурс, а ряд элементов аппаратуры космических аппаратов снят с производства.
КРНС «Цикада» аналогична системе «Цикада-М». В состав системы входят 4 КА, что позволяет при совместном применении сократить дискретность обсерваций.

5.3 Система ARGOS

ARGOS — еще одна спутниковая система, которая использует Доплеровский принцип позиционирования. ARGOS коммерческий проект Французского Национального Центра Космических исследований (CNES), НАСА и Американского Национального Управления по Океанам и Атмосфере (NOAA) и была впервые запущена в 1978 г. Передатчиками управляются пользователи с различных «платформ» (буи, отслеживаемые животные, радиозонды и т. д.), а спутники действуют как приемники (один из двух — Американский метеоспутник TIROS). CNES вычисляет положение и скорость платформ, передает информацию (и счет!) пользователю. Другие такие системы для «подписчиков» включает в себя системы поиска и спасения COSPAS-SARSAT и GEOSTAR. Важное различие состоит в том, что ARGOS по существу спутниковая система слежения, тогда как многие другие системы ( включая GPS) — системы самоуправления.

5.4 Система Галилео

Европейская спутниковая радионавигационная система Галилео разрабатывается по инициативе Европейского Союза и Европейского космического агентства (ЕКА). Галилео должна полностью войти в строй в 2008 г. в результате объединения усилий членов Европейского союза. В проекте предусматривается создание глобальной системы под гражданским управлением. Система должна включать глобальный (космический), региональный и локальный компоненты, а также приемники пользователей и терминалы.

Космический сегмент состоит из 30 спутников, распределенных в трех орбитальных плоскостях с наклонение 56 ° . Рассматриваются другие варианты созвездия Галилео, в частности, с использованием нескольких геостационарных спутников. Высота полета 23616 км, период обращения 14 ч. 04 мин. В запуске планируется выводить от двух до восьми спутников, в зависимости от возможностей ракеты и потребностей группировки. В качестве средств запуска возможно использование ракет-носителей Ариан, Протон и Союз. В космический сегмент входят два Центра контроля, размещаемые в Западной Европе, станции передачи данных и станции мониторинга. Региональный и локальный сегменты представляют инфраструктуру широкозонной и локальной дифференциальных подсистем.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Системы координат и связь между ними. Классификация и виды используемых систем координат

Классификация и виды используемых систем координат

Кинематические характеристики движения центра масс и вращательного движения КА вокруг центра масс зависят от системы координат, в которой изучается его движение. При изучении движения орбитальных объектов и небесных тел применяются прямоугольные, криволинейные и оскулирую- щие системы координат. Криволинейными являются цилиндрические, сферические, эллипсоидальные, параболоидальные координаты.

В зависимости от места положения начала координат системы делятся на:

• • геоцентрические с началом координат в центре масс Земли;
• • топоцентрические — начало координат в точке на поверхности Земли;
• • объектоцентрические — с началом координат в центре масс КА.

В зависимости от выбора направления осей систем по отношению к пространственным ориентирам системы делятся на вращающиеся (неинерциальные) и невращающиеся (абсолютные, инерциальные).

Для инерциальных геоцентрических систем координат необходимо указать момент времени (эпоху), к которому отнесена принятая система координат.

Основными системами координат, используемыми в баллистике, являются:

• 1. Абсолютная геоцентрическая система OXYZ (АГСК), фиксированная на фундаментальную эпоху Т₀. В качестве эпохи Т₀ принята эпоха J2000,0: 2000 г., январь 1, 12 h . Начало системы совпадает с центром масс Земли. Основная плоскость OXY — плоскость среднего экватора эпохи Т₀. Направление ОХ — направление в среднюю точку весеннего равноденствия той же эпохи.
• 2. Гринвичская относительная система координат Oxyz (ГОСК), отнесена к истинному экватору. Её начало совпадает с центром масс Земли. Основная плоскость Оху — плоскость истинного экватора. Опорное направление Ох — линия пересечения плоскости гринвичского меридиана с плоскостью истинного экватора.
• 3. В гринвичской СК сферические координаты — /?,#>, А,

где: R- геоцентрический радиус-вектор;

(р — геоцентрическая широта (угол между радиусом-вектором R точки

и его проекцией на плоскость экватора);

Я — долгота (угол между гринвичским меридианом и меридианом

4. Геодезическая система координат BLH. Основная плоскость системы — плоскость экватора принятого эллипсоида (в России — эллипсоид Красовского). Его центр и малая ось должны как можно точнее совпадать с центром масс и осью вращения Земли. Размеры задаются значениями большой полуоси а и сжатия а.

Опорное направление определяется пересечением гринвичского меридиана с плоскостью экватора. Геодезическая высота точки Н — расстояние от поверхности эллипсоида, отсчитываемое по нормали; геодезическая широта В — угол между нормалью к эллипсоиду и экватором; геодезическая долгота L — угол между опорным направлением и меридианом точки на экваторе, отсчитываемым на восток.

• 5. Топоцентрическая прямоугольная система координат 0%г]?. Начало системы — фазовый центр антенны измерительной станции. Основная плоскость — плоскость горизонта, перпендикулярная к геоцентрическому радиусу-вектору точки начала отсчета и проходит через нее. Опорное направление 0% — направление на север по меридиану начала. Ось Orj — совпадает с направлением геоцентрического радиуса — вектора точки начала системы координат. Ось — направлена на восток.
• 6. Орбитальная прямоугольная система координат O_xrln. Начало системы в центре масс космического аппарата. Ось О/г -направлена по радиусу-вектору КА, ось Oil — по трансверсальному направлению к орбите КА в сторону его движения, ось Ощ — дополняет систему до правой.
• 7. Стартовая система координат (ССК). Начало отсчета совпадает с центром масс PH, находящейся на пусковой установке. Ось OY направлена вертикально по линии отвеса. Ось ОХ находится в плоскости, перпендикулярной оси OY, и развернута на угол А_ст от плоскости меридиана точки старта (направления на север N), называемый азимутом запуска PH. Ось OZ дополняет систему до правой системы.
• 8. Начальная стартовая система координат (НССК) Ox_HCy_HCz_HC. Получается фиксацией стартовой СК в некоторый момент времени 1ф. Переход из НССК в ГОСК, фиксированных на один и тот же момент времени, производится с использованием тех же функциональных преобразований (матрицы перехода), что и из стартовой СК в гринвичскую СК.
• 9. Связанная система координат (СвСК) OxiyjZj. Начало отсчета совпадает с центром масс РБ (КА). Ось Ох, направлена по продольной оси объекта, ось Оу, перпендикулярна плоскости «выведения», ось Oz, дополняет систему до правой.
• 10. Скоростная система координат (СкСК) Ox_vy^z_v. Начало отсчета — центр масс РБ (КА). Ось Oy_v направлена по радиусу-вектору РБ (КА) с началом в центре масс Земли, ось Ox_v находится в плоскости, образуемой радиусом-вектором и вектором скорости набегающего потока, и направлена в сторону, противоположную набегающему потоку. Ось Oz_v дополняет систему до правой.

Переход от одной системы координат к другой проводится с использованием соотношений, записываемых в векторно-матричном виде.

1. Связь гринвичской относительной СК (Oxyz) с абсолютной геоцентрической (OXYZ) фундаментальной эпохи фиксации с учетом неравномерности вращения Земли определяется:

где: Rs — матрица учета суточного вращения Земли;

N — матрица нутации в эпоху (;

Р — матрица прецессии, описывающая переход от среднего равноденствия и экватора стандартной эпохи к экватору эпохи t.

Матрица Rs имеет вид

где: S- значение гринвичского истинного звездного времени в эпоху t.

Матрицы прецессии и нутации учитывают колебания оси вращения

Для обратного перехода от одной системы координат к другой используются транспонированные исходные матрицы перехода.

2. Для связи прямоугольных и сферических координат прямоугольным координатам ставят в соответствие сферические. Связь прямоугольных координат Ь_х, Ь_у, b_z вектора b со сферическими Ь, Xi определяется соотношениями:

Угол gi отсчитывается в плоскости ху от оси л: до проекции вектора b на плоскость ху против хода часовой стрелки, смотря с конца оси +z. Угол Xi считается положительным, если лежит по одну сторону с осью z относительно плоскости ху.

3. Топоцентрическая прямоугольная система координат связана с гринвичской относительной системой соотношениями

где: VgyVqyVg — составляющие вектора скорости в топоцентрической горизонтальной СК;

Х_т, Y_m, Z_m, ф_т, Л_т — соответственно гринвичские прямоугольные и сферические координаты начала топоцентрической системы.

4. Между сферическими геодезическими координатами В, L, Н и геодезическими прямоугольными координатами X, Y, Z существуют соотношения:

где: а и а — соответственно большая полуось и полярное сжатие эллипсоида относимости,

N— радиус кривизны первого вертикала [3.7].

Если геодезические координаты В, L, Н заданы на общем земном эллипсоиде, то прямоугольные координаты X, Y, Z совпадают с гринвичскими координатами х, у, z.

🎬 Видео

Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

05. Пространство и время. Координаты. Вектор перемещения. Радиус вектор.Скачать

Радиус вектор точки геометрияСкачать

Координаты вектора. 9 класс.Скачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Построение проекции вектора на осьСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Разложение вектора по базису. 9 класс.Скачать