Геометрическое место прямых пересекающих две параллельные прямые (8 видео)

Найдите геометрическое место (ГМ) прямых

Скачать
презентациюНазовите прямые, проходящие через вершины куба >>

Упражнение 4. Найдите геометрическое место (ГМ) прямых, пересекающих две данные параллельные прямые. Ответ: Плоскость.

Слайд 5 из презентации «Параллельность прямых в пространстве» к урокам геометрии на тему «Параллельность в пространстве»

Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке геометрии, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Параллельность прямых в пространстве.ppt» можно в zip-архиве размером 177 КБ.

Содержание

Параллельность в пространстве
Введение. Аксиомы стереометрии и их следствие. 5 часов (стр. 7 )
Геометрия Лобачевского
💡 Видео

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Параллельность в пространстве

«Параллельность прямых в пространстве» — Прямые AB и C3D3 параллельны. Сколько имеется пар параллельных прямых. Плоские углы. Всегда ли две не пересекающиеся прямые в пространстве параллельны. Прямые AA1 и CC1 параллельны. Ребра икосаэдра. Прямые AA1 и CC1, проходящие через вершины правильной шестиугольной призмы, параллельны. Прямая, пересекающая одну из параллельных прямых, пересекает и вторую прямую.

«Параллельность прямой и плоскости» — Найти угол между прямыми CM и BD. Задача № 20. Задача № 40. Найти угол между прямыми MD и AC. Свойство 2. Дано: прямая allb, a є ?, b є ?. Доказать:all?. Свойства. 3. Прямая и плоскость не имеют общих точек. 1. Определение. 2. Признак. 3. Свойства. Найти скрещивающиеся прямые. Угол между прямыми. Точки Е,F,M,N – середины ребер.

«Параллельные плоскости» — Стороны AB и BC параллелограмма ABCD пересекают некоторую плоскость. Две плоскости в пространстве называются параллельными, если. Прямая пересекает две стороны треугольника. Каково взаимное расположение данной прямой и второй диагонали? Могут ли прямая и плоскость не иметь общих точек? Взаимное расположение двух плоскостей в пространстве.

«Определение параллельности прямых» — Две прямые. Параллелепипед. Точка. Стороны. Свойство. Взаимное расположение прямых. Метод. Отрезки параллельных прямых. Параллельность плоскостей. Скрещивающиеся прямые. Угол между прямыми. Полуплоскости. Параллельные прямые в пространстве. Плоскость. Взаимное расположение. Признак параллельности. Две параллельные плоскости.

«Теоремы о параллельности плоскостей и прямых» — Теорема о параллельных прямых. Любые три точки лежат в одной плоскости. Провести плоскость. Различные плоскости. Теорема. Аксиомы. Прямая проходит через вершину треугольника. Признак параллельности двух плоскостей. Плоскость. Середина. Параллельные прямые. Пропущенные слова. Способы задания плоскостей.

«Параллельные прямые в пространстве» — Следствия аксиомы параллельных прямых — ? Какие прямые в планиметрии называются параллельными? Аксиома параллельных прямых — ? Каково может быть взаимное расположение прямых в пространстве? Теорема о параллельности трех прямых в пространстве. Какие прямые в пространстве называются параллельными? Параллельные отрезки, параллельные лучи в пространстве.

Видео:Параллельные прямые. 6 класс.Скачать

Введение. Аксиомы стереометрии и их следствие. 5 часов (стр. 7 )

Геометрическое место прямых пересекающих две параллельные прямые

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

5. Геометрическое место прямых, пересекающих одну из скрещивающихся прямых и параллельных другой, есть…

II. Объяснение нового материала.

Пункты учебника (п. 8, 9) можно прочитать вместе с учащимися. Проверить осознанность усвоения теоремы об углах с соноправленными сторонами, можно, попросив учащихся доказать теорему на видоизмененном чертеже, составить план доказательства.

III. Решение задач №№ 44, 45, 47.

Домашнее задание: теория (п. 8 – 9); №№ 46, 97.

Уроки 10–11
АКСИОМЫ СТЕРЕОМЕТРИИ.
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Цель: повторить теорию, подготовить учащихся к контрольной работе.

I. Устная работа.

1. Прямая пересекает две стороны треугольника. Лежит ли она в плоскости этого треугольника?

2. Прямая пересекает вершину треугольника. Лежит ли она в плоскости этого треугольника?

3. Три вершины параллелограмма лежат в плоскости. Принадлежит ли четвертая вершина параллелограмма этой плоскости?

4. Хорда окружности принадлежит плоскости. Верно ли утверждение, что и вся окружность лежит в этой плоскости?

5. Две пересекающиеся хорды окружности принадлежат плоскости. Верно ли утверждение, что любая точка окружности принадлежит этой плоскости?

6. Сколько плоскостей можно провести через: три различные точки; две различные точки; через прямую и не лежащую на ней точку; через две параллельные прямые?

7. Верно ли утверждение: любые три точки принадлежат плоскости; через любые три точки проходит единственная плоскость?

8. Известно, что прямая параллельна плоскости. Параллельна ли она любой прямой, лежащей в этой плоскости? Может ли данная прямая пересечь какую-либо прямую, лежащую в плоскости?

9. Средняя линия трапеции лежит в плоскости α. Пересекают ли основания трапеции эту плоскость?

10. Прямая а параллельна линии пересечения плоскостей α и β. Каково взаимное расположение а и α; а и β?

11. Прямая b непараллельна линии пересечения плоскостей α и β. Каково взаимное расположение b и α; b и β?

12. Сколько можно провести через данную точку: прямых, параллельных данной плоскости; плоскостей, параллельных данной прямой?

13. Стороны АВ и ВС параллелограмма ABCD пересекают некоторую плоскость. Докажите, что прямые AD и DC пересекают эту плоскость.

14. Плоскость α параллельна одной из двух параллельных прямых. Каково взаимное расположение второй прямой и плоскости α?

15. Сторона АВ параллелограмма ABCD лежит в плоскости α. Докажите, что сторона CD параллельна этой плоскости.

16. Прямая пересекает плоскость. Можно ли в плоскости провести прямую, параллельную данной прямой?

17. Две прямые параллельны одной плоскости. Можно ли утверждать, что эти прямые параллельны?

18. Каким может быть взаимное расположение двух прямых, из которых одна параллельна некоторой плоскости, а другая пересекает эту плоскость?

19. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b быть параллельными? Пересекаться?

20. Может ли каждая из двух скрещивающихся прямых быть параллельна третьей прямой?

21. Прямая, не лежащая в плоскости параллелограмма, параллельна одной из его диагоналей. Каково взаимное расположение данной прямой и второй диагонали?

22. Как могут быть расположены прямая и плоскость, если данная прямая и некоторая прямая, лежащая в этой плоскости, скрещиваются?

II. Решение задач.

Варианты I и IV рассмотреть в классе. Варианты II и III дать домой для самостоятельного решения.

1. На рисунке точки А, С, М и Р лежат в плоскости α, а точка В α.

Постройте точку пересечения прямой MP с плоскостью АВС.

2. Треугольники АВС и ADC лежат в разных плоскостях и имеют общую сторону АС. Точка Е лежит на стороне АВ, F – на стороне ВС, причем EF параллельна плоскости ADC. Р – середина AD, а K – середина DC.

2) Каково взаимное положение прямых РK и АВ? Чему равен угол между этими прямыми, если АВС = 40° и ВСА = 80°?

3. Плоскости α и β пересекаются по прямой m. Прямая а лежит в плоскости α. Каково возможное взаимное положение прямой а и плоскости β ? Сделайте рисунок и поясните.

4*. Используя рисунок, постройте линию пересечения плоскости EFM с плоскостью α. Поясните.

1. На рисунке точки Е и F лежат в плоскости β, а М – в плоскости α. Постройте линии пересечения плоскости EFM с плоскостями α и β. Поясните.

2. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.

1) Докажите, что BCFE – параллелограмм.

2) Каково взаимное положение прямых EF и АВ? Чему равен угол между ними, если АВС = 150°? Поясните.

3. Отрезок АВ параллелен плоскости α, а отрезок CD лежит в этой плоскости, причем AB = CD. Можно ли утверждать, что четырехугольник ABDC – параллелограмм? Поясните.

4*. Плоскости α и β пересекаются по прямой m. Прямая АВ лежит в плоскости α, а CD – в плоскости β.

Что нужно изменить в условии, чтобы прямые АС и BD могли пересекаться?

В каком случае это возможно?

1. На рисунке точки А и В лежат в плоскости α, а С – в плоскости β.

Постройте линии пересечения плоскости АВС с плоскостями α и β.

2. Треугольники ABC и DCE лежат в разных плоскостях и имеют общую вершину С, АВ || DE.

1) Постройте линию пересечения плоскостей АВС и DCE. Поясните.

2) Каково взаимное положение прямых АВ и DF, где F лежит на стороне CE? Чему равен угол между этими прямыми, если FED = 60° и DFE = 100°? Поясните.

3. Прямая а параллельна плоскости α, точка М и прямая с лежат в плоскости α (М с). Через точку М проведена прямая b, параллельная а. Каково взаимное положение прямых b и с? Поясните.

4*. Плоскости α и β пересекаются по прямой m. Прямая АВ лежит в плоскости α, а CD – в плоскости β.

Что нужно изменить в условии, чтобы прямые EF и MK могли быть параллельными? Поясните.

1. На рисунке точки А, С, E и F лежат в плоскости α, а точка В α.

Постройте точку пересечения прямой EF с плоскостью АВС.

2. Трапеция ABCD (AD и ВС – основания) и треугольник AED имеют общую сторону AD и лежат в разных плоскостях. Точка М лежит на стороне АЕ, а Р – на стороне DE, причем МР параллельна плоскости трапеции.

2) Каково взаимное положение прямых МР и АВ? Чему равен угол между этими прямыми, если АВС = 110°? Поясните.

3. Плоскости α и β пересекаются по прямой m. Прямая а лежит в плоскости α, а b – в плоскости β. Какие возможны взаимные положения прямых а и b? Сделайте рисунок и поясните.

4*. Используя рисунок, постройте линию пересечения плоскости МРK с плоскостью α.

Урок 12
КОНТРОЛЬНАЯ РАБОТА № 1

1. В каком случае три точки в пространстве не определяют положение плоскости, проходящей через эти точки?

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Геометрия Лобачевского

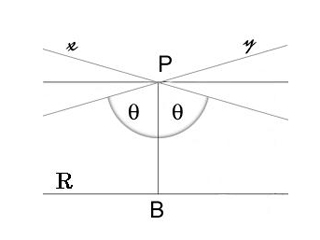
Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.

Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.

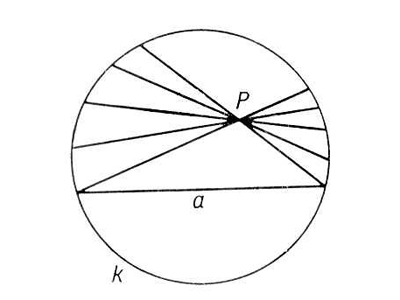
И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.

Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.

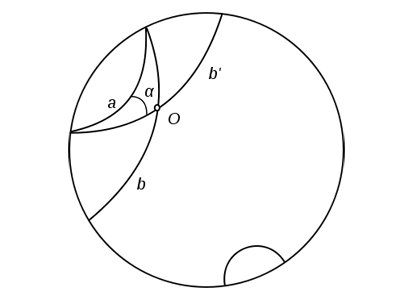
Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.

Аксиома параллельности Лобачевского выглядит следующим образом:

Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.

Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.

Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.

В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».

Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».

Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:

x 2 + y 2 + z 2 = c 2 t 2 ,

при делении на t 2 , то есть для скорости света, даёт уравнение сферы в пространстве с координатами v_x, v_y, v_z, которые являются составляющими скорости света по осям х, у, z.

Преобразование Лоренца сохраняет эту сферу, а поскольку они линейны, переводят прямые пространства скоростей в прямые. Из этого следует, (согласно модели Клейна) что в пространстве скоростей внутри сферы радиуса с , значит есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.