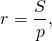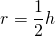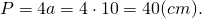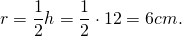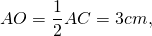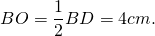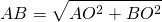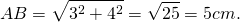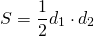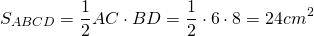Где лежит центр вписанной окружности в параллелограмме

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

1. Не во всякий четырехугольник можно вписать окружность.
2. Если у четырехугольника суммы длин его противолежащих
   сторон равны, то окружность, может быть, вписана (Теорема Пито).
3. Центр вписанной окружности и середины двух
   диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
4. Точка пересечения биссектрис — это центр вписанной окружности.
5. Точка касания — это точка, в которой соприкасается
   окружность и любая из сторон четырехугольника.
6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

• Треугольник
  
• Четырехугольник
  
• Многоугольник
  

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

В параллелограмм вписана окружность

Если в условии задачи сказано, что в параллелограмм вписана окружность, то что сразу можно сказать об этом параллелограмме?

Для этого надо вспомнить, когда в четырехугольник можно вписать окружность. Это можно сделать лишь в том случае, если суммы противолежащих сторон четырехугольника равны.

Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).

Следовательно, если известно, что в параллелограмм можно вписать окружность, сразу можно сделать вывод, что все его стороны равны, и для него справедливы все свойства ромба. Если же дополнительно сказано, что хотя бы один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.

Радиус вписанной в ромб окружности можно найти по формуле

где S — площадь ромба, p — его полупериметр;

или как половину высоты ромба

1) В параллелограмм вписана окружность. Найти периметр параллелограмма, если одна из его сторон равна 10 см.

Из всех параллелограммов вписать окружность можно только в ромб (и квадрат). У ромба все стороны равны.

2) В параллелограмм вписана окружность. Найти её радиус, если высота параллелограмма равна 12 см.

Из параллелограммов вписать окружность можно в ромб (и квадрат). Радиус вписанной в ромб (и квадрат) окружности равен половине его высоты:

3) В параллелограмм вписана окружность. Найти её радиус, если диагонали параллелограмма равны 6 см и 8 см.

Из всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).

Пусть ABCD — ромб, AC=6 см, BD=8 см.

Рассмотрим треугольник AOB.

По теореме Пифагора

полупериметр — p=2a=2∙AB=25=10 см.

Следовательно, радиус вписанной окружности равен

Окружность вписана в параллелограмм теорема

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6cf6d5a6ee840c42 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

1. Не во всякий четырехугольник можно вписать окружность.
2. Если у четырехугольника суммы длин его противолежащих
   сторон равны, то окружность, может быть, вписана (Теорема Пито).
3. Центр вписанной окружности и середины двух
   диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
4. Точка пересечения биссектрис — это центр вписанной окружности.
5. Точка касания — это точка, в которой соприкасается
   окружность и любая из сторон четырехугольника.
6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

• Треугольник
  
• Четырехугольник
  
• Многоугольник
  

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Четырехугольники, вписанные в окружность. Теорема Птолемея

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

💥 Видео