Функция график которой является прямая параллельная оси абсцисс (5 видео)

Прямые на координатной плоскости

Линейная функция

График линейной функции

Прямые, параллельные оси ординат

Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

Содержание

Линейная функция
График линейной функции
Прямые, параллельные оси ординат
Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
ГДЗ учебник по алгебрее 7 класс Макарычев. 16. Линейная функция и ее график. Номер №320
Решение а
Решение б
Решение в
Решение г
Линейная функция
🌟 Видео

Видео:ГРАФИК ФУНКЦИЙ — Сдвиги Графика Функции, Как строить Графики Функции // Алгебра 8 классСкачать

Линейная функция

Линейной функцией называют функцию, заданную формулой

y = kx + b,

(1)

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

Видео:7 класс. Задайте формулой линейную функцию, параллельную данной и проходящую через точку NСкачать

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

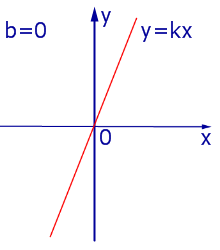Рис.1

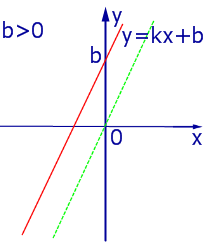Рис.2

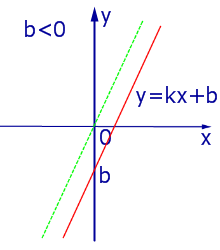Рис.3

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

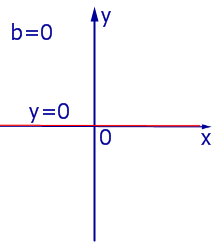Рис.4

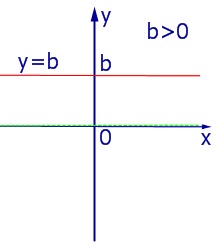Рис.5

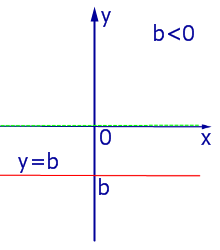Рис.6

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b₁ и y = kx + b₂ ,

имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны .

имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.

y = kx + b₁ и

перпендикулярны при любых значениях свободных членов.

Угловой коэффициент прямой линии

y = kx

(2)

равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).

Рис.10

Рис.11

Рис.12

Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .

При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Прямые, параллельные оси ординат

Прямые, параллельные оси Oy , задаются формулой

x = c ,

(3)

где c – произвольное число, и изображены на рис. 13, 14, 15.

Рис.13

Рис.14

Рис.15

Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;

Видео:Дан график производной Найти абсциссу точки в которой касательная к графику функции парал-на оси ХСкачать

Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

px + qy = r ,

(4)

где p, q, r – произвольные числа.

В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

что и требовалось.

В случае, когда получаем:

откуда вытекает, что уравнение (4) задает прямую линию вида (3).

В случае, когда q = 0, p = 0, уравнение (4) имеет вид

0 = r ,

(5)

и при r = 0 его решением являются точки всей плоскости:

В случае, когда уравнение (5) решений вообще не имеет.

Замечание 2 . При любом значении r₁ , не совпадающем с r прямая линия, заданная уравнением

px + qy = r₁ ,

(6)

параллельна прямой, заданной уравнением (4) .

Замечание 3 . При любом значении r₂ прямая линия, заданная уравнением

– qx + py = r₂ ,

(7)

перпендикулярна прямой, заданной уравнением (4) .

Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и

параллельной к прямой
4x + 5y = 7 ; (8)
перпендикулярной к прямой (8).

В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде

4x + 5y = r₁ ,

(9)

где r₁ – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство

Итак, уравнение прямой, параллельной к прямой

В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде

– 5x + 4y = r₂ ,

(10)

где r₂ – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

ГДЗ учебник по алгебрее 7 класс Макарычев. 16. Линейная функция и ее график. Номер №320

(Задача−исследование.) Дана линейная функция y = kx + 4 . При каком значении k график этой функции:
а) параллелен графику прямой пропорциональности y = −x;
б) не пересекает ось абсцисс;
в) пересекает ось абсцисс в точке с абсциссой 3 ;
г) проходит через точку пересечения графиков функций y = 12 − x и y = x + 4 ?
Обсудите ответы на поставленные вопросы.

Решение а

График функции y = kx + 4 будет параллелен графику y = −x при k = − 1 .

Решение б

График функции y = kx + 4 не пересекает ось абсцисс при k = 0 .

Решение в

Пересекает ось абсцисс в точке ( 3 ; 0 ):
y = kx + 4
0 = 3 k + 4
3 k = − 4

Решение г

12 − x = x + 4
2 x = 8
x = 4
y = 12 − x = 12 − 4 = 8
Точка пересечения графиков y = 12 − x и y = x + 4 имеет координаты ( 4 ; 8 ).
y = kx + 4
8 = 4 k + 4
4 k = 8 − 4
4 k = 4
k = 1

Видео:Линейная функция и ее график. 7 класс.Скачать

Линейная функция

Линейная функция – функция вида , где и – некоторые числа.

Число называется угловым коэффициентом прямой (и равняется тангенсу угла наклона прямой к положительному направлению оси абсцисс). Число называется свободным членом . График линейной функции является прямой линией, откуда и вытекает название.

Графики линейных функций, имеющие один и тот же угловой коэффициент , параллельны друг другу ( см. рис. слева (ниже)).

Графики функций, коэффициенты и которых связаны следующим образом: , перпендикулярны друг другу (рис. справа).

Частные случаи:

1)
Тогда , графиком является прямая, параллельная оси абсцисс, проходящая, в частности, через точку (рис. слева (ниже))
2)
Тогда (прямая пропорциональность), графиком является прямая, проходящая через начало координат (рис. справа).

Строить график линейной функции можно двумя основными способами:

1) Через две точки

Одну из точек обычно берут . Эта точка сразу же видна, ведь свободный член в формуле задает ординату точки пересечения с осью (оy). Вторую точку выбираем любую (), лишь бы удобно было в ней считать соответствующее значение .