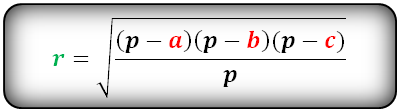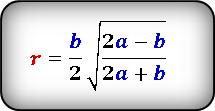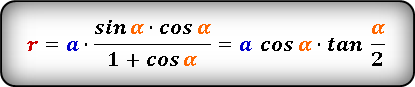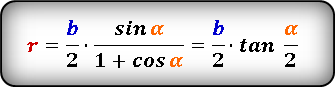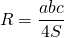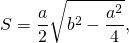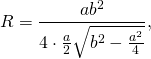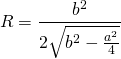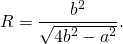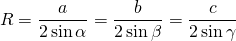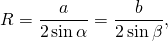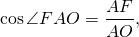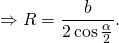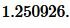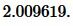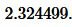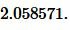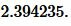- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Радиус описанной окружности равнобедренного треугольника
- Вписанная и описанная окружность равнобедренного треугольника формула
- Все формулы для радиуса вписанной окружности
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- 1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- 2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- 3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- 4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- 5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
- 📽️ Видео
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

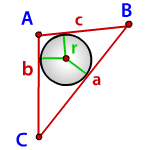
Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

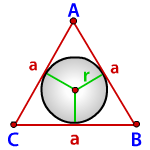
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
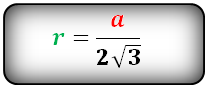
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

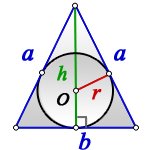
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
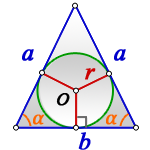
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Радиус описанной окружности равнобедренного треугольника
Радиус описанной окружности равнобедренного треугольника можно найти по одной из общих формул радиуса окружности, описанной около треугольника.
Используя свойства равнобедренного треугольника, можно также получить дополнительные формулы.
I. Радиус описанной около треугольника окружности можно найти по формуле
Площадь равнобедренного треугольника через длину основание a и боковую сторону b можно найти по формуле
соответственно, формула для нахождения радиуса описанной окружности для равнобедренного треугольника принимает вид:
верна и для равнобедренного треугольника.
Радиус описанной около равнобедренного треугольника окружности:
где a — основание, b — боковая сторона, α — угол при вершине, β — угол при основании.
III. Радиус описанной окружности в равнобедренном треугольнике можно найти непосредственно, без использования общих формул.
Например, в прямоугольном треугольнике AOF AO=R, AF=b/2, ∠FAO=α/2. Отсюда
IV. В равнобедренном тупоугольном треугольнике центр описанной окружности лежит вне треугольника, напротив его вершины.
Радиус находят по тем же формулам, что и для остроугольного треугольника.
V. В равнобедренном прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, радиус равен половине гипотенузы (то есть половине основания треугольника).
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная и описанная окружность равнобедренного треугольника формула
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Все формулы для радиуса вписанной окружности
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Видео:Радиус вписанной и описанной окружности в равностороннем треугольникеСкачать

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Радиус описанной окружностиСкачать

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
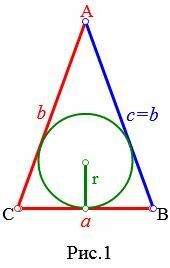 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
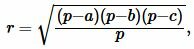 | (1) |
где полупериметр p вычисляется из формулы:
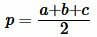 . . | (2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac ) ( small =frac , ) | (3) |
| ( small p-a=frac -a ) ( small =frac , ) | (4) |
| ( small p-b=p-c=frac -b ) ( small =frac . ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
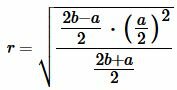 , , |
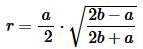 . . | (6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
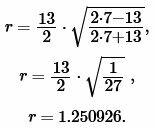 |
Ответ:
Видео:Формулы для радиусов вписанной и описанной окружностей треугольника Геометрия 9классСкачать

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
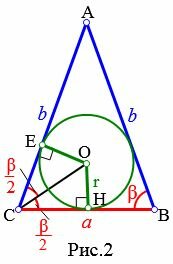 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac . ) Для прямоугольного треугольника OCH можно записать:
| ( small frac =frac >=mathrm frac .) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac cdot mathrm frac .) | (8) |
| ( small r=frac cdot frac .) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
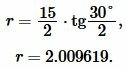 |
Ответ:
Видео:Формулы равностороннего треугольника #shortsСкачать

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
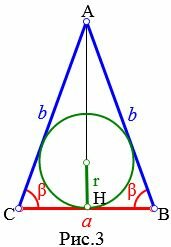 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| ( small frac =frac > = cos beta .) |
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=frac cdot mathrm frac =frac cdot mathrm frac ) ( small =b cos beta cdot mathrm frac ) |
| ( small r=b cdot cos beta cdot mathrm frac ) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac ) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
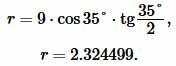 |
Ответ:
Видео:Формула радиуса описанной окружности треугольника. Геометрия 9 классСкачать

4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
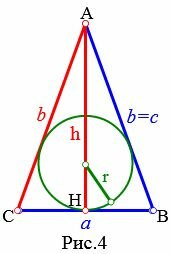 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
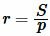 , , | (13) |
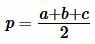 | (14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| ( small left( frac right)^2=b^2-h^2 ) |
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac ) ( small =frac ) ( small =frac +b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac ) ( small =frac > > ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
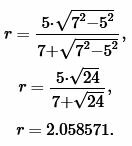 |
Ответ:
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
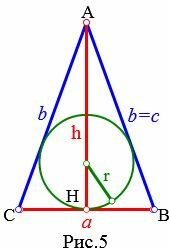 |
Из формулы (15) найдем b:
| ( small b^2-h^2=left( frac right)^2 ) |
| ( small b^2= frac +h^2 ) |
| ( small b= frac cdot sqrt ) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=frac > >) ( small =frac +h^2-h^2>> cdot sqrt + sqrt +h^2-h^2>>) ( small = large frac > cdot sqrt +frac >) |
| ( small r=large frac >) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
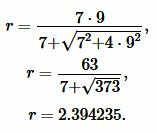 |
Ответ:
📽️ Видео
Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

Формула радиуса вписанной окружности треугольника. Геометрия 9 классСкачать