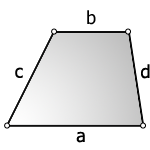
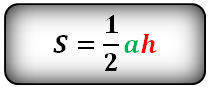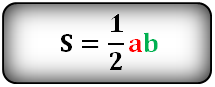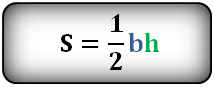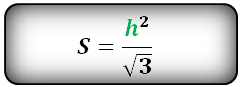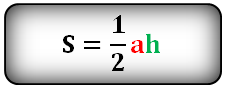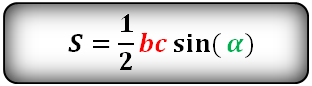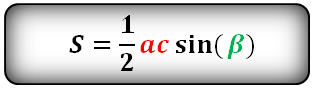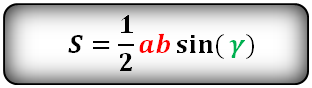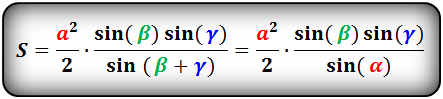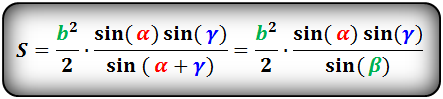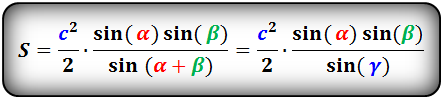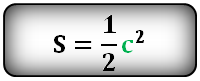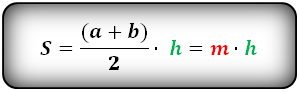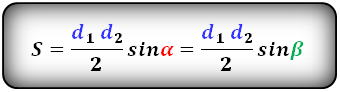- Формулы, признаки и свойства правильного многоугольника
- Признаки правильного многоугольника
- Основные свойства правильного многоугольника
- Формулы правильного n-угольника
- Формулы длины стороны правильного n-угольника
- Формула стороны правильного n-угольника через радиус вписанной окружности
- Формула стороны правильного n-угольника через радиус описанной окружности
- Формулы радиуса вписанной окружности правильного n-угольника
- Формула радиуса вписанной окружности n-угольника через длину стороны
- Формула радиуса описанной окружности правильного n-угольника
- Формула радиуса описанной окружности n-угольника через длину стороны
- Формулы площади правильного n-угольника
- Формула площади n-угольника через длину стороны
- Формула площади n-угольника через радиус вписанной окружности
- Формула площади n-угольника через радиус описанной окружности
- Формула периметра правильного многоугольника
- Формула периметра правильного n-угольника
- Формула определения угла между сторонами правильного многоугольника
- Формула угла между сторонами правильного n-угольника
- Правильный треугольник
- Формулы правильного треугольника
- Формула стороны правильного треугольника через радиус вписанной окружности
- Формула стороны правильного треугольника через радиус описанной окружности
- Формула площади правильного треугольника через длину стороны
- Формула площади правильного треугольника через радиус вписанной окружности
- Формула площади правильного треугольника через радиус описанной окружности
- Углы между сторонами правильного треугольника
- Правильный четырехугольник
- Формулы правильного четырехугольника
- Формула стороны правильного четырехугольника через радиус вписанной окружности
- Формула стороны правильного четырехугольника через радиус описанной окружности
- Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
- Формула радиуса описанной окружности правильного четырехугольника через длину стороны
- Формула площади правильного четырехугольника через длину стороны
- Формула площади правильного четырехугольника через радиус вписанной окружности
- Формула площади правильного четырехугольника через радиус описанной окружности
- Углы между сторонами правильного четырехугольника
- Правильный шестиугольник
- Формулы правильного шестиугольник
- Формула стороны правильного шестиугольника через радиус вписанной окружности
- Формула стороны правильного шестиугольника через радиус описанной окружности
- Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
- Формула радиуса описанной окружности правильного шестиугольника через длину стороны
- Формула площади правильного шестиугольника через длину стороны
- Формула площади правильного шестиугольника через радиус вписанной окружности
- Формула площади правильного шестиугольника через радиус описанной окружности
- Углы между сторонами правильного шестиугольника
- Правильный восьмиугольник
- Площадь правильного многоугольника
- Онлайн калькулятор — площадь правильного многоугольника
- Формулы площадей многоугольников вписанных в окружность
- Правильный многоугольник
- Формулы, признаки и свойства правильного многоугольника
- Признаки правильного многоугольника
- Основные свойства правильного многоугольника
- Формулы правильного n-угольника
- Формулы длины стороны правильного n-угольника
- Формула стороны правильного n-угольника через радиус вписанной окружности
- Формула стороны правильного n-угольника через радиус описанной окружности
- Формулы радиуса вписанной окружности правильного n-угольника
- Формула радиуса вписанной окружности n-угольника через длину стороны
- Формула радиуса описанной окружности правильного n-угольника
- Формула радиуса описанной окружности n-угольника через длину стороны
- Формулы площади правильного n-угольника
- Формула площади n-угольника через длину стороны
- Формула площади n-угольника через радиус вписанной окружности
- Формула площади n-угольника через радиус описанной окружности
- Формула периметра правильного многоугольника
- Формула периметра правильного n-угольника
- Формула определения угла между сторонами правильного многоугольника
- Формула угла между сторонами правильного n-угольника
- Правильный треугольник
- Формулы правильного треугольника
- Формула стороны правильного треугольника через радиус вписанной окружности
- Формула стороны правильного треугольника через радиус описанной окружности
- Формула площади правильного треугольника через длину стороны
- Формула площади правильного треугольника через радиус вписанной окружности
- Формула площади правильного треугольника через радиус описанной окружности
- Углы между сторонами правильного треугольника
- Правильный четырехугольник
- Формулы правильного четырехугольника
- Формула стороны правильного четырехугольника через радиус вписанной окружности
- Формула стороны правильного четырехугольника через радиус описанной окружности
- Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
- Формула радиуса описанной окружности правильного четырехугольника через длину стороны
- Формула площади правильного четырехугольника через длину стороны
- Формула площади правильного четырехугольника через радиус вписанной окружности
- Формула площади правильного четырехугольника через радиус описанной окружности
- Углы между сторонами правильного четырехугольника
- Правильный шестиугольник
- Формулы правильного шестиугольник
- Формула стороны правильного шестиугольника через радиус вписанной окружности
- Формула стороны правильного шестиугольника через радиус описанной окружности
- Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
- Формула радиуса описанной окружности правильного шестиугольника через длину стороны
- Формула площади правильного шестиугольника через длину стороны
- Формула площади правильного шестиугольника через радиус вписанной окружности
- Формула площади правильного шестиугольника через радиус описанной окружности
- Углы между сторонами правильного шестиугольника
- Правильный восьмиугольник
- Площадь правильного многоугольника
- Онлайн калькулятор — площадь правильного многоугольника
- Формулы площадей всех основных фигур
- 1. Формула площади круга через радиус или диаметр
- 2. Формула расчета площади треугольника
- 3. Площадь треугольника, формула Герона
- 4. Площадь прямоугольного треугольника по катетам
- 5. Как вычислить площадь равнобедренного треугольника ?
- 6. Площадь равностороннего треугольника равна:
- 7. Найти площадь треугольника, угол и две стороны
- 8. Площадь треугольника по стороне и двум углам, формула.
- 9. Формула расчета площади прямоугольника
- 10. Как рассчитать площадь квадрата через диагональ или сторону
- 11. Формулы площади параллелограмма
- 12. Площадь произвольной трапеции
- 13. Площадь равнобедренной трапеции
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы, признаки и свойства правильного многоугольника
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.
a 1 = a 2 = a 3 = … = a n-1 = a n ,
α 1 = α 2 = α 3 = … = α n-1 = α n
где a1 … an — длины сторон правильного многоугольника,
α 1 … α n — внутренние углы между стронами правильного многоугольника.
Основные свойства правильного многоугольника
- Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
- Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
- Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольникаO.
- Сумма всех углов n-угольника равна: 180° · n — 2
- Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
- В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формулы правильного n-угольника
Формулы длины стороны правильного n-угольника
Формула стороны правильного n-угольника через радиус вписанной окружности
a = 2 · r · tg 180° n (через градусы),
a = 2 · r · tg π n (через радианы)
Формула стороны правильного n-угольника через радиус описанной окружности
a = 2 · R · sin 180° n (через градусы),
a = 2 · R · sin π n (через радианы)
Формулы радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны
r = a : 2 · tg 180° n (через градусы),
r = a : 2 · tg π n (через радианы)
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны
R = a : 2 · sin 180° n (через градусы),
R = a : 2 · sin π n (через радианы)
Формулы площади правильного n-угольника
Формула площади n-угольника через длину стороны
Формула площади n-угольника через радиус вписанной окружности
Формула площади n-угольника через радиус описанной окружности
Формула периметра правильного многоугольника
Формула периметра правильного n-угольника
Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.
Формула определения угла между сторонами правильного многоугольника
Формула угла между сторонами правильного n-угольника
Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Правильный треугольник
Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Формулы правильного треугольника
Формула стороны правильного треугольника через радиус вписанной окружности
Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.
Формула стороны правильного треугольника через радиус описанной окружности
Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.
Формула площади правильного треугольника через длину стороны
Формула площади правильного треугольника через радиус вписанной окружности
Формула площади правильного треугольника через радиус описанной окружности
Углы между сторонами правильного треугольника
Видео:2190 угол между стороной правильного n угольника вписанного в окружностьСкачать

Правильный четырехугольник
Правильный четырехугольник — это квадрат.
Формулы правильного четырехугольника
Формула стороны правильного четырехугольника через радиус вписанной окружности
Сторона правильного четырехугольника равна двум радиусам вписанной окружности.
Формула стороны правильного четырехугольника через радиус описанной окружности
Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.
Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.
Формула радиуса описанной окружности правильного четырехугольника через длину стороны
Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.
Формула площади правильного четырехугольника через длину стороны
Площадь правильного четырехугольника равна квадрату стороны четырехугольника.
Формула площади правильного четырехугольника через радиус вписанной окружности
Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.
Формула площади правильного четырехугольника через радиус описанной окружности
Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.
Углы между сторонами правильного четырехугольника
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Правильный шестиугольник
Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.
Формулы правильного шестиугольник
Формула стороны правильного шестиугольника через радиус вписанной окружности
Формула стороны правильного шестиугольника через радиус описанной окружности
Длина стороны правильного шестиугольника равна радиусу описанной окружности.
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
Формула радиуса описанной окружности правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности
Углы между сторонами правильного шестиугольника
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Правильный восьмиугольник
Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Площадь правильного многоугольника
Видео:Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Онлайн калькулятор — площадь правильного многоугольника
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Правильный многоугольник так же называют правильным n-угольником, где n — это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).
В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью.
Около любого правильного многоугольника можно описать окружность.
Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Формулы площадей многоугольников вписанных в окружность
Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Правильный многоугольник
Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Формулы, признаки и свойства правильного многоугольника
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.
a 1 = a 2 = a 3 = … = a n-1 = a n ,
α 1 = α 2 = α 3 = … = α n-1 = α n
где a1 … an — длины сторон правильного многоугольника,
α 1 … α n — внутренние углы между стронами правильного многоугольника.
Основные свойства правильного многоугольника
- Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
- Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
- Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольникаO.
- Сумма всех углов n-угольника равна: 180° · n — 2
- Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
- В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .
Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Формулы правильного n-угольника
Формулы длины стороны правильного n-угольника
Формула стороны правильного n-угольника через радиус вписанной окружности
a = 2 · r · tg 180° n (через градусы),
a = 2 · r · tg π n (через радианы)
Формула стороны правильного n-угольника через радиус описанной окружности
a = 2 · R · sin 180° n (через градусы),
a = 2 · R · sin π n (через радианы)
Формулы радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны
r = a : 2 · tg 180° n (через градусы),
r = a : 2 · tg π n (через радианы)
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны
R = a : 2 · sin 180° n (через градусы),
R = a : 2 · sin π n (через радианы)
Формулы площади правильного n-угольника
Формула площади n-угольника через длину стороны
Формула площади n-угольника через радиус вписанной окружности
Формула площади n-угольника через радиус описанной окружности
Формула периметра правильного многоугольника
Формула периметра правильного n-угольника
Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.
Формула определения угла между сторонами правильного многоугольника
Формула угла между сторонами правильного n-угольника
Видео:Геометрия 9 класс (Урок№26 - Построение правильных многоугольников.)Скачать

Правильный треугольник
Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Формулы правильного треугольника
Формула стороны правильного треугольника через радиус вписанной окружности
Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.
Формула стороны правильного треугольника через радиус описанной окружности
Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.
Формула площади правильного треугольника через длину стороны
Формула площади правильного треугольника через радиус вписанной окружности
Формула площади правильного треугольника через радиус описанной окружности
Углы между сторонами правильного треугольника
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Правильный четырехугольник
Правильный четырехугольник — это квадрат.
Формулы правильного четырехугольника
Формула стороны правильного четырехугольника через радиус вписанной окружности
Сторона правильного четырехугольника равна двум радиусам вписанной окружности.
Формула стороны правильного четырехугольника через радиус описанной окружности
Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.
Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.
Формула радиуса описанной окружности правильного четырехугольника через длину стороны
Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.
Формула площади правильного четырехугольника через длину стороны
Площадь правильного четырехугольника равна квадрату стороны четырехугольника.
Формула площади правильного четырехугольника через радиус вписанной окружности
Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.
Формула площади правильного четырехугольника через радиус описанной окружности
Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.
Углы между сторонами правильного четырехугольника
Видео:Площадь многоугольника через радиус вписанной окружностиСкачать

Правильный шестиугольник
Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.
Формулы правильного шестиугольник
Формула стороны правильного шестиугольника через радиус вписанной окружности
Формула стороны правильного шестиугольника через радиус описанной окружности
Длина стороны правильного шестиугольника равна радиусу описанной окружности.
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
Формула радиуса описанной окружности правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности
Углы между сторонами правильного шестиугольника
Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Правильный восьмиугольник
Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Площадь правильного многоугольника
Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Онлайн калькулятор — площадь правильного многоугольника
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Правильный многоугольник так же называют правильным n-угольником, где n — это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).
В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью.
Около любого правильного многоугольника можно описать окружность.
Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Видео:Задание № 1094 - Геометрия 9 класс (Атанасян)Скачать

Формулы площадей всех основных фигур
Видео:Геометрия 9 класс (Урок№23 - Длина окружности.)Скачать

1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
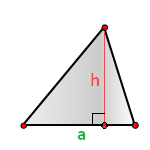
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
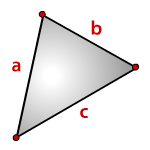
3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
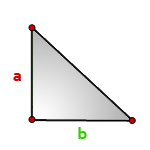
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
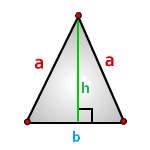
5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):

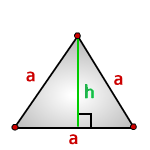
6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
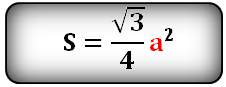
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
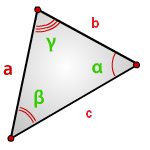
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
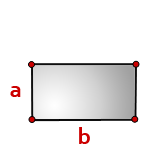
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
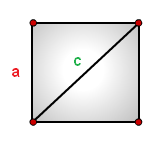
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
12. Площадь произвольной трапеции
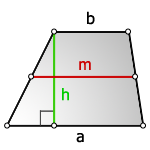
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
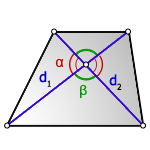
2. Формула площади трапеции через диагонали и угол между ними
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):