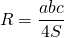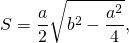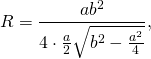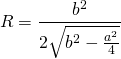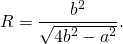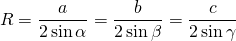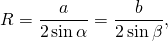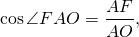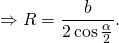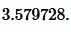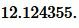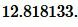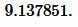Радиус описанной окружности равнобедренного треугольника можно найти по одной из общих формул радиуса окружности, описанной около треугольника.
Используя свойства равнобедренного треугольника, можно также получить дополнительные формулы.
I. Радиус описанной около треугольника окружности можно найти по формуле
Площадь равнобедренного треугольника через длину основание a и боковую сторону b можно найти по формуле
соответственно, формула для нахождения радиуса описанной окружности для равнобедренного треугольника принимает вид:
верна и для равнобедренного треугольника.
Радиус описанной около равнобедренного треугольника окружности:
где a — основание, b — боковая сторона, α — угол при вершине, β — угол при основании.
III. Радиус описанной окружности в равнобедренном треугольнике можно найти непосредственно, без использования общих формул.
Например, в прямоугольном треугольнике AOF AO=R, AF=b/2, ∠FAO=α/2. Отсюда
IV. В равнобедренном тупоугольном треугольнике центр описанной окружности лежит вне треугольника, напротив его вершины.
Радиус находят по тем же формулам, что и для остроугольного треугольника.
V. В равнобедренном прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, радиус равен половине гипотенузы (то есть половине основания треугольника).
- Радиус описанной окружности около равнобедренного треугольника онлайн
- 1. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и боковая сторона b=c
- 2. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и противолежащий угол A
- 3. Радиус окружности описанной около равнобедренного треугольника, если известны боковая сторона b=c треугольника и угол между боковыми сторонами A
- 4. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и прилежащий угол B=C
- Равнобедренные треугольники
- 📸 Видео
Видео:№690. Найдите основание равнобедренного треугольника, если центр вписанной в него окружностиСкачать

Радиус описанной окружности около равнобедренного треугольника онлайн
С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

1. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и боковая сторона b=c
Пусть известны основание a равнобедренного треугольника и боковая сторона b=c. Найдем радиус описанной окружности около равнобедренного треугольника. На странице Радиус окружности описанной около треугольника онлайн была выведена формула вычисления радиуса R описанной около любого треугольника окружности:
| ( small R=frac<large 4 cdot sqrt >. ) | (1) |
где p вычисляется из формулы:
| ( small p= frac. ) | (2) |
Учитывая, что у нас треугольник равнобедренный, т.е. b=c, имеем:
| ( small p= frac=b+ frac, ) | (3) |
| ( small p-a= b- frac, ) | (4) |
| ( small p-b= frac, ) | (5) |
Подставляя (3)−(5) в (1) и учитывая, что b=c, получим:
| ( small R=frac<large 4 cdot frac cdot sqrt<left ( b+fracright)left ( b-fracright)>> ) ( small =frac<large 2 cdot sqrt< b^2-frac>> ) ( small =frac< sqrt> ,) |
| ( small R=frac< sqrt>. ) | (6) |
Пример 1. Известны основание ( small a=7 ) и боковая сторона ( small b=frac ) равнобедренного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (6).
Подставим значения ( small a=7 ) и ( small b=frac ) в (6):
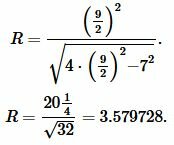 |
Ответ:
Видео:Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать

2. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и противолежащий угол A
Пусть известны сторона a и противолежащий угол A. Формула для нахождения радиуса окружности описанной около равнобедренного треугольника по основанию и противолежащему углу аналогична формуле для нахождения радиуса окружности описанной около произвольного треугольника:
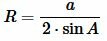 . . | (7) |
Пример 2. Сторона основание равнобедренного треугольника равна:( small a=21 ) а противолежащий угол ( small angle A=60°.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения ( small a=21 ) и ( small angle A=60° ) в (7):
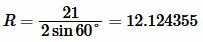 . . |
Ответ:
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

3. Радиус окружности описанной около равнобедренного треугольника, если известны боковая сторона b=c треугольника и угол между боковыми сторонами A
Пусть известны боковая сторона b=c равнобедренного треугольника и угол между боковыми сторонами A. Найдем радиус описанной окружности около равнобедренного треугольника.
На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известных сторонах и углу между ними:
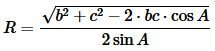 . . | (8) |
Подставляя в (8) c=b, получим:
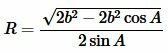 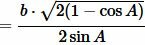 |
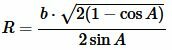 . . | (9) |
Пример 3. Известны основание ( small a=21 ) равнобедренного треугольника и угол между боковыми сторонами: ( small angle A=70°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (9). Подставим значения ( small a=21; ) и ( small angle A=70° ) в (9):
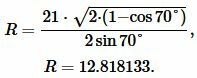 |
Ответ:
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

4. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и прилежащий угол B=C
Пусть известны основание a равнобедренного треугольника и прилежащие к ней угол B=C. Найдем радиус описанной окружности около треугольника. На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известной стороне и прилежащим двум углам:
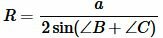 . . | (10) |
Подставляя ( small C=B ) в (10), получим требуемую формулу:
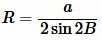 . . | (11) |
Пример 4. Известны основание равнобедренного треугольника ( small a=14 ) и прилежащий к ней угол: ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (11). Подставим значения ( small a=14 ) и ( small angle B=25° ) в (11):
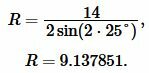 |
Ответ:
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

Равнобедренные треугольники
Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
$∠BCD$ — внешний угол треугольника $АВС$.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$.
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$cos BOA= — cos BOC;$
$ctg BOA= — ctg BOC.$
В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.
Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)
Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$
Рассмотрим прямоугольный треугольник $АНС$.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:
Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:
Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
В треугольнике $АВС$ $ВС=16, sin∠A=/$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
Далее подставим числовые данные и найдем $R$
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
📸 Видео
Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Геометрия Боковые стороны равнобедренного треугольника равны 4, радиус описанной окружности равенСкачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

Вариант 55, № 8. Радиус окружности, описанной около равнобедренного треугольникаСкачать

Радиус описанной окружностиСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Центр описанной окружности равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

ЕГЭ 6 номер. Нахождение диаметра описанной окружности около равнобедренного треугольникаСкачать

2080 Боковые стороны равнобедренного треугольника равны 569 основание равно 462Скачать

Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать
Нахождение радиуса окружности, описанной около равнобедренного треугольника.Скачать

Задание 24 Площадь вписанного равнобедренного треугольникаСкачать