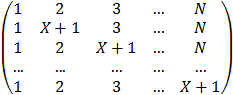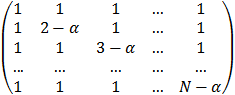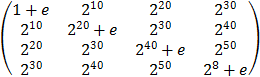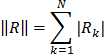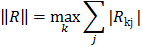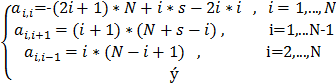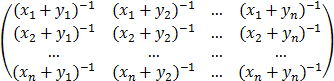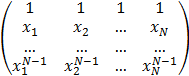Формирование матрицы по заданному вектору (6 видео)

Процедура формирования матрицы. Норма вектора и матриц

Содержание

Страницы работы
Содержание работы
Формирование векторов и матриц
Особенности задания векторов и матриц
Объединение малых матриц в большую
Формирование матрицы по заданному вектору
🔥 Видео

Страницы работы

Содержание работы

Составить процедуру формирования матрицы A(N,N) , зависящей от параметра X

A =

Используя эту процедуру, подпрограммы DECOMP и SOLVE , найти A -1 для N=5 и значений X = 1.1 , 1.001 , 1.00001 , для каждого X вычислить матрицу R=AA -1 — E и ее норму.

Написать процедуру формирования матрицы A по заданному вектору B

A = 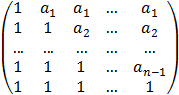, B = ( a₁ , a₂ , …, a_n-1 ) T

Задавая n=5 , a₁ = 4 , a₂ = 3 , a₃ = 2 , a₄ = var = 1.5 ; 1.01 ; 1.001 ; 1.0001 и вычисляя A -1 с помощью DECOMP и SOLVE , найти нормы матриц

R = AA -1 — E для всех вариантов a₄ .

Составить процедуру формирования матрицы A(N,N) , зависящей от параметра a

A =

Решить систему Ay = B , где B_k = k+cos(k) , используя программы DECOMP и SOLVE , для a = 0.9999 ; 0.99999 ; 0.999999 и для N=4. Сравнить результаты решения с двойной и стандартной точностью.

Составить процедуру формирования матрицы A(e) по заданному параметру e

A =

Для e = 10 , 1 , 0.1 сравнить решения систем A T Ax=A T b и Ax=b для

b = (1, 2, 3, 4) T в этих трех случаях. Сравнение результатов проводить по норме невязок R = Ax-b и R = A T Ax-A T b . Норму вектора вычислять по формуле

Составить процедуру вычисления нормы матрицы R = AA -1 — E , где

Используя DECOMP и SOLVE , вычислить A -1 по заданной матрице

A =

Для N=4 и четырех значений s = -1.01 , -1.001 , -1.0001 , -1.00001 вычислить нормы матриц R.

1. Построить процедуру вычисления матрицы по заданным векторам x, y:

A =

2. Для x_k = 1/cos(k) , k=1, …, 5 и y_k = k , k=1, …, 4 решить три системы уравнений Az = b , где y₅ = 1.01 , 1.001 , 1.0001 , а компоненты вектора b вычисляются по формуле b_k = 2 k . Сравнить решения, полученные с двойной и стандартной точностями, используя программы DECOMP и SOLVE.

Составить процедуру формирования матриц H и A по формулам

H = , A = bE + H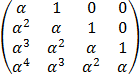

Решить ряд линейных систем Ax = b , где взять a = 10 , b = 0.1 , 0.01 , 0.5 , 1.0 ; b_k = tg(k) , используя программы DECOMP и SOLVE. Сравнить решения, получаемые со стандартной и двойной точностью.

Составить процедуру вычисления по заданной матрице A(N,N) матрицы R = A -1 A — E и ее нормы .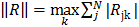

Построить три матрицы A при x_k = (1+cos(k))/sin 2 (k) , k=1, …, 4 и

x₅ = (1+cos(1))/sin 2 (1+e) для трех значений e = 0.001 , 0.00001 , 0.000001 и N=5.

A =

Исследовать зависимость погрешности вычисления 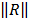от e .

1. Составить процедуру вычисления матрицы R и ее нормы 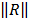по заданной матрице A : R = A -1 A — E ,

2. Построить несколько вариантов матрицы A , зависящей от параметра d = 1.01 , 1.001 , 1.0001

A_ik = 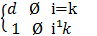, N = 5 .

Вычисляя A -1 по процедурам DECOMP и SOLVE , исследовать зависимость 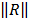от d .

Составить процедуру вычисления матрицы

Решить ряд линейных систем Ax=b , где b_k = cos(k) , a₁ = 1.01 , a₂ = 1.001 , a₃ = var = 1.01 , 1.001 , 1.0001 , используя DECOMP и SOLVE . Сравнить решения, полученные с обычной и двойной точностью.

Составить процедуру вычисления матрицы

A =

Полагая y_k = cos(k) , k=1, …, 5 ; x_k = 1/(1+k) , k = 1, …, 4 и задавая три варианта x₅ = 0.9 , 0.99 , 0.999 , исследовать поведение матрицы R = A -1 A — E и ее нормы 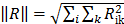от параметра x₅ . Для вычисления A -1 использовать программы DECOMP и SOLVE.

Построить процедуру вычисления элементов матриц H и A :

H = , A = bE + H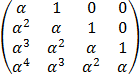

Для a = 2 и b = 0.1 , 0.01 , 0.001 вычислить матрицу R = A -1 A — E и ее норму 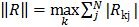. Объяснить результаты.

1. Составить процедуру вычисления матрицы A вида

A =

2. Используя ее, решить несколько раз линейную систему Az=b , где N=5, b_k = 2 k + cos(k) , k = 1, …, 5 ; x_k = k , k=1,…,4 и x₅ = 1.1 , 1.01 , 1.001 , 1.0001 . Системы решать с обычной и двойной точностью, используя программы DECOMP и SOLVE. Сделать необходимые выводы.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Формирование векторов и матриц

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Особенности задания векторов и матриц

MATLAB — система, специально предназначенная для проведения сложных вычислений с векторами, матрицами и массивами — в том числе многомерными.

При этом она по умолчанию предполагает, что каждая заданная переменная — это вектор, матрица или массив. Все определяется конкретным значением переменной. Например, если задано х=1, то это значит, что X — это вектор с единственным элементом, имеющим значение 1. Если надо задать вектор из трех элементов, то их значения следует перечислить в квадратных скобках, разделяя пробелами. Так, например, присваивание

задает вектор V, имеющий три элемента со значениями 1, 2 и 3. После ввода вектора система выводит его на экран дисплея.

Задание матрицы требует указания нескольких строк. Для разграничения строк используется знак ; (точка с запятой). Этот же знак в конце ввода предотвращает вывод матрицы или вектора (и вообще любой операции) на экран дисплея. Так, ввод

» М= [ 1 2 3; 4 5 6; 7 8 9];

задает квадратную матрицу, которую можно вывести:

Возможен ввод элементов матриц и векторов в виде арифметических выражений, содержащих любые доступные системе функции, например:

» V= [2+2/(3 + 4) exp (5) sqrt(10)];

2.2857 148.4132 3.1623

Для указания отдельного элемента вектора или матрицы используются выражения вида v(i) илим(1, j ). Например, если задать

то результат будет равен 5. Если нужно присвоить элементу м (i, j) новое значение х, следует использовать выражение

Например, если элементу м(2, 2) надо присвоить значение 10, следует записать

Вообще говоря, в тексте программ MATLAB лучше не использовать буквы i и j как индексы, так как i и j — обозначение квадратного корня из —1. Но можно использовать I и J.

Выражение м (i) с одним индексом дает доступ к элементам матрицы, развернутым в один столбец. Такая матрица образуется из исходной, если подряд выписать ее столбцы. Следующий пример поясняет такой доступ к элементам матрицы м:

» М=[1 2 3; 4 5 6; 7 8 9]

Возможно задание векторов и матриц с комплексными элементами, например:

» СМ = [1 2; 34]+ i*[5 6; 7 8]

» СМ = [l+5*i 2+6*1; 3 + 7*i 4+8*i]

Это создает матрицу:

1.0000 + 5.0000i 2.0000 + 6.00001
3.0000 + 7.00001 4.0000 + 8.00001

Наряду с операциями над отдельными элементами матриц и векторов система позволяет производить операции умножения, деления и возведения в степень сразу над всеми элементами, то есть над массивами. Для этого перед знаком операции ставится точка. Например, оператор * означает умножение для векторов или матриц, а оператор . * — поэлементное умножение всех элементов массива. Так, если м — матрица, то м. *2 даст матрицу, все элементы которой умножены на скаляр — число 2. Впрочем, для умножения матрицы на скаляр оба выражения — м*2 и м.*2 — оказываются эквивалентными.

Имеется также ряд особых функций для задания векторов и матриц. Например, функция magic (п) задает магическую матрицу размера п х п, у которой сумма всех столбцов, всех строк и даже диагоналей равна одному и тому же числу:

16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1

Уже сама по себе возможность создания такой матрицы с помощью простой функции magic заинтересует любителей математики. Но векторных и матричных функций в системе множество, и мы их детально рассмотрим в дальнейшем. Напомним, что для стирания переменных из рабочей области памяти служит команда clear.

Видео:Матрицы и векторыСкачать

Объединение малых матриц в большую

Описанный способ задания матриц позволяет выполнить операцию конкатенации — объединения малых матриц в большую. Например, создадим вначале магическую матрицу размера 3×3:

Теперь можно построить матрицу, содержащую четыре матрицы:

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Формирование матрицы по заданному вектору

Операции с векторами и матрицами

Создание стандартных матриц

Создание векторов равноотстоящих точек в линейном и логарифмическом масштабах

Создание массивов со случайными элементами

Изменение порядка расположения элементов матриц

Вычисление сумм и произведений

Изменение формы матриц

Выделение треугольных частей матриц

Вычисление тестовых матриц

Матрицы представляют собой самые распространенные объекты системы MATLAB. Ниже описываются основные операции с матрицами. По обилию матричных операторов и функций MATLAB является лидером среди массовых систем компьютерной математики.

Создание матриц с заданными свойствами

Создание единичной матрицы

Для создания единичной матрицы (она обычно обозначается как Е) служит функция eye:

еуе(n) — возвращает единичную матрицу размера nrn;

eye(m.n) или еуе([m n]) — возвращают матрицу размера mm с единицами по диагонали и нулями в остальных ячейках;

eye(size(A)) — возвращает единичную матрицу того же размера, что и А.

Единичная матрица не определена для многомерных массивов. Так, функция у = eye([2,3,4]) при попытке ее вычисления приведет к ошибке.

Пример использования функции eye:

Создание матрицы с единичными элементами

Для создания матриц, все элементы которых — единицы, используется функция ones:

ones(n) — возвращает матрицу размера nхn, все элементы которой — единицы. Если п — не скаляр, то появится сообщение об ошибке;

ones(m.n) или ones([m п]) — возвращают матрицу размера mxn, состоящую из единиц;

ones(dl.d2,d3. ) или ones([dl1 d2 d3. ]) — возвращает массив из единиц с размером d1xd2xd3x. ;

ones(size(A)) — возвращает массив единиц той же размерности и размера, что и А. Матрица с единичными элементами в отличие от единичной матрицы в MATLAB определена и для многомерных массивов.

Создание матрицы с нулевыми элементами

Иногда нужны матрицы, все элементы которых — нули. Следующая функция обеспечивает создание таких матриц:

zeros(п) — возвращает матрицу размера nхn, содержащую нули. Если n — не скаляр, то появится сообщение об ошибке;

zeros(m.n) или zeros([m n]) — возвращают матрицу размера mxn, состоящую из нулей;

zeros(d1.d2,d3. ) или zeros([d1.d2.d3. ]) — возвращают массив из нулей размера d1xd2xd3x. ;

zeros(size(A)) — возвращает массив нулей того же размера и размерности, что и А.

Создание линейного массива равноотстоящих точек

Функция linspace формирует линейный массив равноотстоящих узлов. Это подобно оператору :, но дает прямой контроль над числом точек. Применяется в следующих формах:

llnspace(a.b) — возвращает линейный массив из 100 точек, равномерно распределенных между а и b;

linspace(a,b,n) — генерирует п точек, равномерно распределенных в интервале от а до b.

Columns I through 7

4.0000 5.2308 6.4615 7.6923 8.9231 10.153811.3846

Columns 8 through 14

Создание вектора равноотстоящих в логарифмическом масштабе точек

Функция logspace генерирует вектор равноотстоящих в логарифмическом масштабе точек. Она особенно эффективна при создании вектора частот. Это логарифмический эквивалент оператора : и функции linspace:

logspace(a.b) — возвращает вектор-строку из 50 равноотстоящих в логарифмическом масштабе точек между декадами 10^0 и 10^b;

logspace(a.b.n) — возвращает n точек между декадами 10^a и 10^b;

logspace(a.pi) — возвращает точки в интервале между 10^a и п. Эта функция очень полезна в цифровой обработке сигналов.

Все аргументы функции logspace должны быть скалярными величинами. Пример:

Columns 1 through 7

Columns 8 through 14

Создание массивов со случайными элементами

р = randperm(n) — возвращает случайные перестановки целых чисел 1:n в векторе-строке. Пример:

Функция rand генерирует массивы случайных чисел, значения элементов которых равномерно распределены в промежутке (0, 1):

rand(n) — возвращает матрицу размера nхn. Если n — не скаляр, то появится сообщение об ошибке;

rand(m.n) или rand([m п]) — возвращают матрицу размера mxn;

rand(m.n,p. ) или rand([m n р. ]) — возвращает многомерный массив;

rand(size(A)) — возвращает массив того же размера и размерности, что и А, с элементами, распределенными по равномерному закону;

rand (без аргументов) — возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет равномерный закон распределения;

rand(‘ state’) — возвращает вектор с 35 элементами, содержащий текущее состояние генератора случайных чисел с равномерным распределением. Для изменения состояния генератора можно применять следующие формы этой функции:

rand(‘state’ .s) — устанавливает состояние в s;

rand( ‘state’ ,0) — сбрасывает генератор в начальное состояние;

rand( ‘state’. j) — для целых j, устанавливает генератор в j-е состояние;

rand( ‘state’ ,sum(100*clock)) — каждый раз сбрасывает генератор в состояние, зависящее от времени.

0.9501 0.8913 0.8214

0.2311 0.7621 0.4447

0.6068 0.4565 0.6154

0.4860 0.0185 0.7919

Проверить равномерность распределения случайных чисел можно, построив большое число точек на плоскости со случайными координатами. Это делается с помощью следующих команд:

Полученный при этом график показан на рис. 10.1. Нетрудно заметить, что точки довольно равномерно распределены на плоскости, так что нет оснований не доверять заданному закону распределения координат точек.

Рис. 10.1. Случайные точки с равномерным распределением координат на плоскости

Функция randn генерирует массив со случайными элементами, распределенными по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением, равным 1:

randn(n) — возвращает матрицу размера nхn. Если n — не скаляр, то появится сообщение об ошибке;

randn(m.n) или randn([m n]) — возвращают матрицу размера mxn;

randn(m,n,p. ) или randn([m n р. ]) — возвращает массив с элементами, значения которых распределены по нормальному закону;

randn(size(A)) — возвращает массив того же размера, что и А, с элементами, распределенными по нормальному закону;

randn (без аргументов) — возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет нормальное распределение;

randn( ‘state’) — возвращает двухэлементный вектор, включающий текущее состояние нормального генератора. Для изменения состояния генератора можно применять следующие формы этой функции:

randn(‘state’,s) — устанавливает состояние в s;

randn(‘state’ ,0) — сбрасывает генератор в начальное состояние;

randn(‘state’, j) — для целых j устанавливает генератор в J-e состояние;

randn(‘state’, sum( 100*clock)) — каждый раз сбрасывает генератор в состояние, зависящее от времени.

-0.4326 -1.1465 0.3273

-1.6656 1.1909 0.1746

0.1253 1.1892 -0.1867

0.2877 -0.0376 0.7258

Проверить распределение случайных чисел по нормальному закону можно, построив гистограмму распределения большого количества чисел. Например, следующие команды

строят гистограмму (рис. 10.2) из 100 столбцов для 10 000 случайных чисел с нормальным распределением.

Рис. 10.2. Гистограмма для 10 000 нормально распределенных чисел в 100 интервалах

Из рисунка видно, что огибающая гистограммы действительно близка к нормальному закону распределения.

В пакете расширения Statistics Toolbox можно найти множество статистических функций, в том числе для генерации случайных чисел с различными законами распределения и определения их статистических характеристик.

Конкатенацией называют объединение массивов, которое реализует следующая функция.

С = cat (dim, А, В) — объединяет массивы А и В в соответствии со спецификацией размерности dim и возвращает объединенный массив; dim = 1 — горизонтальная конкатенация, dim = 2 — вертикальная, dim = 3 — многомерный массив размерности 3 и т. д.;

С = cat(dim,Al,A2,A3,A4. ) объединяет все входные массивы (А1, А2, A3, А4 и т. д.) в соответствии со спецификацией размерности dim и возвращает объединенный массив;

cat(2.A,B) — это то же самое, что и [А,В],асаt(,А,В) —то же самое, что и [А; В]. При записи cat (dim, С (:)) или cat (dim, С. field) эта функция применима к массивам ячеек или структур, содержащим численные матрицы. Пример:

Создание матриц с заданной диагональю

Свойства матриц сильно зависят от их диагональных элементов. Следующая функция MATLAB позволяет создавать специальные типы матриц с заданными диагональными элементами:

X = diag(v.k) — для вектора v, состоящего из п компонентов, возвращает квадратную матрицу X порядка n+abs(k) с элементами v на k-й диагонали, при k=0 -это главная диагональ (из левого верхнего угла матрицы в правый нижний угол), при k>0 — одна из диагоналей (диагональ в терминологии MATLAB — это линия, параллельная главной диагонали) выше главной диагонали, при k

X = diag(v) — помещает вектор v на главную диагональ (то же. что и в предыдущем случае при k=0);

v = diag(X.k) — для матрицы X возвращает вектор-столбец, состоящий из элементов n-й диагонали матрицы X;

v = diag(X) — возвращает главную диагональ матрицы X (то же, что и в предыдущем случае при k=0).