Если вектора а и в не коллинеарны то любой вектор с можно (3 видео)

выберите верные утверждения

помогите решить геометрию, пожалуйста! (
А) если вектор С можно разложить по векторам А и Б т. е представить в виде С=ХА+УВ, где Х и У-некоторые числа, то векторы а и в, с компланарны
Б) при сложении трех некомпланарных вектором можно пользоваться правилом параллелепипеда
В) три вектора, среди которых имеются два коллинеарных, компланарны
Г) два любых сонаправленых вектора некомпланарны

1)а, б, в, г
2)а, б, г
3)а, б, в
4)а, в, г

все, кроме г, правильно.
сонаправленные векторы коллинеарны (т. е. лежат на одной прямой) , а значит и компланарны (лежат в одной плоскости).. . да и вообще любые два вектора компланарны

Содержание

Коллинеарность векторов, условия коллинеарности векторов.
Условия коллинеарности векторов
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Примеры задач на коллинеарность векторов в пространстве
04.07. Линейная зависимость векторов
Линейная зависимость векторов
📺 Видео

Видео:№914. Докажите, что если векторы а и 6 не коллинеарны, то: а) векторы a+b и a - b не коллинеарныСкачать

Коллинеарность векторов, условия коллинеарности векторов.

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).

Если вектора а и в не коллинеарны то любой вектор с можно

рис. 1

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = < a_x ; a_y ; a_z > и b = < na_x ; na_y ; na_z >. Найдем их векторное произведение

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Примеры задач на коллинеарность векторов

Примеры задач на коллинеарность векторов на плоскости

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:

a_x	=	a_y	.
b_x		b_y

Вектора a и b коллинеарны т.к.	1	=	2	.
	4		8

Вектора a и с не коллинеарны т.к.	1	≠	2	.
	5		9

Вектора с и b не коллинеарны т.к.	5	≠	9	.
	4		8

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

n =	b_y	=	6	= 2
	a_y		3

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

a_x	=	a_y	.
b_x		b_y

3	=	2	.
9		n

Решим это уравнение:

n =	2 · 9	= 6
	3

Ответ: вектора a и b коллинеарны при n = 6.

Примеры задач на коллинеарность векторов в пространстве

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:

a_x	=	a_y	=	a_z	.
b_x		b_y		b_z

Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12

Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12

Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

n =	b_y	=	6	= 2
	a_y		3

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

a_x	=	a_y	=	a_z	.
b_x		b_y		b_z

3	=	2	=	m
9	=	n	=	12

Из этого соотношения получим два уравнения:

3	=	2
9	=	n

3	=	m
9	=	12

Решим эти уравнения:

n =	2 · 9	= 6
	3

m =	3 · 12	= 4
	9

Ответ: вектора a и b коллинеарны при n = 6 и m = 4.

Видео:№354. Докажите, что если векторы a + b и a - b не коллинеарны, то: а) векторы а и b не коллинеарныСкачать

04.07. Линейная зависимость векторов

Линейная зависимость векторов

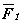
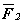
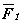
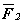
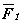
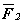
Пусть даны три силы , , , лежащие в одной плоскости. Можно ли любую из них выразить через две другие? Эта задача очень часто встречается в физике. Если и не лежат на одной прямой (рис. 3.15, а), то сила может быть представлена через , и по правилу параллелограмма:

Рис. 3.15. Различные случаи расположения сил.

Если же и лежат на одной прямой, то эту задачу решить не удастся (рис. 3.15, б). Решение задачи окажется невозможным и в том случае, когда сила находится вне плоскости, которую образуют силы , , если они не лежат на одной прямой (рис. 3.15, в). Чтобы понять, почему это происходит, перейдем от геометрической иллюстрации этой задачи к ее строгому математическому анализу, основанному на понятии линейной зависимости векторов и исследовании свойств таких систем векторов.

Где – векторы, а – скаляры, называется ЛИНЕЙНОЙ КОМБИНАЦИЕЙ ВЕКТОРОВ. Его смысл состоит в том, что над системой векторов производятся линейные операции, введенные выше, в результате выполнения которых получается некоторый новый вектор, возможно даже нулевой, если, например, все множители . А если не все равны нулю, может ли их линейная комбинация обратиться в нуль? Оказывается, что условия, определяющие эту возможность, разделяют векторы на две принципиально различные группы.

Система векторов , среди которых есть ненулевые, называется ЛИНЕЙНО ЗАВИСИМОЙ, если их линейная комбинация обращается в нулевой вектор при условии, что Не все скалярные множители равны нулю, то есть

Система векторов называется ЛИНЕЙНО НЕЗАВИСИМОЙ, если их линейная комбинация обращается в нулевой вектор только при условии, что Все скалярные множители равны нулю, т. е.

Очевидно, если в системе векторов есть нулевой вектор, то она линейно зависима. Для доказательства этого факта достаточно в равенстве

Взять все коэффициенты равными нулю, за исключением одного – стоящего перед нулевым вектором (он может принимать любое отличное от нуля значение). Это и будет означать линейную зависимость данной системы векторов.

Если система из n векторов включает в себя m линейно зависимых, то она линейно зависима. Действительно, пусть первые m векторов линейно зависимы. Тогда в равенстве

Хотя бы один из скалярных коэффициентов отличен от нуля. Записав формально равенство

Где не все равны нулю, получим, что система векторов линейно зависима.

Рис. 3.16. Коллинеарные
Векторы.

Как геометрически представить себе линейно зависимые и линейно независимые векторы? Введем для этого два определения.

Векторы называются КОЛЛИНЕАРНЫМИ (рис. 3.16), если они лежат на параллельных прямых.

Нулевой вектор считается коллинеарным любому вектору.

Приведя эти векторы к общему началу, получим, что они располагаются на одной прямой.

Векторы, лежащие в параллельных плоскостях, называются КОМПЛАНАРНЫМИ (рис. 3.17). Нулевой вектор считается компланарным любой системе компланарных векторов.

Рис. 3.17. Компланарные векторы.

Если привести их к общему началу, то они окажутся расположенными в одной плоскости.

Из этих определений следует, что коллинеарность векторов можно рассматривать для системы, состоящей из двух или более векторов, а компланарность – для трех и более векторов.

Действительно, когда число векторов более одного, их приведение к одной прямой осуществимо не всегда. Для коллинеарных векторов этого удается добиться.

Термин «коллинеарность» характеризует взаимное расположение векторов, поэтому коллинеарность одного вектора лишена смысла.

Будут ли коллинеарные векторы компланарны? Будут ли компланарные векторы коллинеарны?

Аналогично, два вектора путем свободного переноса всегда можно расположить в одной плоскости. Поэтому они всегда компланарны. Этого может не быть, если число векторов больше двух. Если же векторы компланарны, то их всегда можно привести в одну плоскость.

Оказывается, коллинеарность и компланарность векторов неразрывно связаны с их линейной зависимостью. Мы докажем сейчас теоремы, которые соединяют эти понятия и служат предпосылками для введения центрального понятия всей математики – СИСТЕМЫ КООРДИНАТ.

ТЕОРЕМА 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Слова «тогда и только тогда», как известно, означают, что имеет место прямая и обратная теоремы. Сформулируем их и докажем.

Необходимость. Если два вектора линейно зависимы, то они коллинеарны.

ДОКАЗАТЕЛЬСТВО. Пусть векторы и линейно зависимы. Тогда в равенстве

Хотя бы один из скалярных множителей или отличен от нуля. Пусть для определенности . Тогда

Где , что означает коллинеарность векторов и .

Достаточность. Если два вектора коллинеарны, то они линейно зависимы.

ДОКАЗАТЕЛЬСТВО. Пусть векторы и коллинеарны. Тогда, очевидно, они связаны соотношением

Это означает, что линейная комбинация векторов и обращается в нулевой вектор, причем скалярный множитель при векторе не равен нулю, то есть система векторов и линейно зависима.

Наряду с доказанной теоремой, могут быть сформулированы еще две, являющиеся ее следствиями.

Сформулируйте эти утверждения с помощью предикатов.

Следствие 1. Если два вектора не являются линейно зависимыми, то они не будут коллинеарны.

Следствие 2. Если два вектора не являются коллинеарными, то они не будут линейно зависимы.

ТЕОРЕМА 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Необходимость. Если три вектора линейно зависимы, то они компланарны.

Рис. 3.18. Связь
между линейной
зависимостью
и компланарностью.

ДОКАЗАТЕЛЬСТВО. Пусть векторы , и линейно зависимы (рис. 3.18). Тогда в равенстве

Хотя бы один из скалярных множителей , или отличен от нуля. Пусть для определенности . Тогда

То есть вектор – диагональ параллелограмма, построенного на векторах и как на сторонах (по правилу сложения векторов). Но векторы и , а также И попарно коллинеарны. Следовательно, и лежат в плоскости этого же параллелограмма, то есть , и – компланарны.

В случае коллинеарности векторов и компланарность , и очевидна.

Достаточность. Если три вектора компланарны, то они линейно зависимы.

Рис. 3.19. Связь между компланарностью и линейной зависимостью векторов.

ДОКАЗАТЕЛЬСТВО. Пусть , и компланарны (рис. 3.19), то есть они лежат в одной плоскости и хотя бы два из них, например, и , неколлинеарны. После приведения системы векторов к общему началу вектор можно разложить по направлениям неколлинеарных векторов и , то есть представить его в виде суммы векторов, лежащих на прямых, задаваемых векторами и :

Но , , поэтому

или .

Поскольку имеется хотя бы один скалярный множитель, отличный от нуля, то , и линейно зависимы.

Могут ли быть среди трех некомпланарных векторов два коллинеарных?

Следствие 1. Если три вектора не являются линейно зависимыми, то они не будут компланарны.

Следствие 2. Если три вектора не являются компланарными, то они не будут линейно зависимы.

ТЕОРЕМА 3. Всякий вектор может быть единственным образом разложен по трем некомпланарным векторам.

Теорема означает, что если векторы , и некомпланарны и вектор произволен, то существует единственное представление

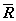
ДОКАЗАТЕЛЬСТВО. Приведем векторы , , и к общему началу (рис. 3.20). Пусть точка L – конец вектора , а точка М – определяет пересечение вспомогательной прямой LM, параллельной вектору , с плоскостью векторов и . Рассмотрим вспомогательные отрезки . Тогда, по правилу сложения векторов,

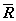
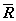
Рис. 3.20. Разложение вектора по трем
некомпланарным
направлениям.

Но векторы и , и , и коллинеарны, поэтому

. (3.1)

Покажем, что это разложение единственно. Предположим противное, что существует другое представление 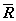через векторы , И :

(3.2)

И хотя бы один из коэффициентов не равен соответствующему коэффициенту . Пусть для определенности . Тогда, вычитая из (3.1) равенство (3.2), получим:

Полученное соотношение означает, что линейная комбинация векторов , и равна нулевому вектору, но скалярный коэффициент при векторе отличен от нуля, то есть векторы , и линейно зависимы, а потому компланарны, что противоречит условию теоремы. Следовательно, предположение о справедливости равенства (3.2) наряду с равенством (3.1), неверно, то есть разложение (3.1) единственно.

Следствие. Любые четыре вектора в пространстве линейно зависимы.

Действительно, если , и некомпланарны, то из равенства (3.1) следует:

Скалярный коэффициент при векторе 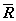не равен нулю. Следовательно, четыре вектора в пространстве линейно зависимы.

Если же какие-то три из векторов , , , компланарны, то они будут линейно зависимы, а значит приведут к линейной зависимости всю систему векторов.

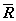
Если какие-то два из четырех векторов коллинеарны, то это означает их линейную зависимость и, следовательно, линейную зависимость всех четырех векторов.

Таким образом, любые четыре вектора в пространстве линейно зависимы.

Вернемся теперь к задачам, поставленным в начале параграфа. Если силы и лежат на одной прямой и силу необходимо выразить через эти векторы, то ясно, что подобная задача неразрешима, так как всякая линейная комбинация сил и есть некоторый вектор

Лежащий на этой прямой и неколлинеарный вектору .

Если две из трех сил коллинеарны, то их можно параллельным переносом привести в одну плоскость, а значит они линейно зависимы. В их линейной комбинации, приравненной к нулю, есть хотя бы один коэффициент, отличный от нуля, что позволяет выразить одну силу через две другие. Если же силы , и представляют собой неколлинеарные друг другу векторы, то, располагаясь в одной плоскости, они образуют линейно зависимую систему векторов, что обеспечивает возможность выразить одну из них через две другие.

Если векторы линейно зависимы, то всякий ли вектор можно выразить через остальные?

Когда одна из сил, например , лежит вне плоскости, образуемой силами и , то система векторов , , становится некомпланарна, а значит, линейно независимой, поэтому между ними возможно лишь соотношение: