Если в пространстве одна из двух параллельных прямых скрещивается с третьей прямой то

Понятие о параллельных прямых

Прямые (a) и (b) являются параллельными в трехмерном пространстве только в том случае, если они находятся в одной плоскости и не пересекаются.

Если рассмотреть примеры, то параллельные прямые мы можем наблюдать как противоположные края у прямоугольного или квадратного стола, железнодорожные рельсы и шпалы, провода линий электропередач, линии в тетради в полоску и прочее. Таких примеров из реального мира можно привести очень много.

Другими вариантами прямых, расположенных в 3D-пространстве, есть их скрещивание и пересечение. Пересекающимися есть прямые, имеющие общую точку, она же и есть точкой пересечения. Скрещивающимися есть прямые, расположенные в разных плоскостях и не параллельные между собой.

Есть ряд теорем, описывающих поведение параллельных прямых в пространстве. Рассмотрим их подробнее.

Теоремы о параллельности двух прямых

1. если две прямые в пространстве перпендикулярные к одной плоскости, то они параллельные между собой;
2. через точку в пространстве, что не расположена на заданной прямой, возможно провести лишь одну прямую, параллельную заданной.

Доказательство теоремы : Через прямую a и точку (M) , не находящуюся на данной прямой, проведем плоскость ∝. Эта плоскость определяется заданной прямой a и точкой (M) , то есть она однозначно определена.

Для доказательства этой теоремы применим евклидовую аксиому из планиметрии про параллельные прямые.
Таким образом, через точку (M) возможно проложить лишь одну прямую, параллельную прямой (a) , и ее существование доказано. Назовем эту прямую (b) .
Два отрезка будут параллельными при их расположении на параллельных прямых.

Свойства параллельных прямых в пространстве

Некоторые свойства пересекаются с вышеизложенными теоремами, но все же рассмотрим их все:

1. имея две параллельных прямых, одна из которых параллельная третьей прямой, можно утверждать, что вторая тоже будет параллельна третьей;
2. если из двух параллельных прямых одна пересекает некую плоскость, то и вторая так же будет ее пересекать. Это свойство является леммой про две параллельные прямые в пространстве, ее применяют при обоснованиях различных геометрических теорем;
3. при помощи двух параллельных прямых можно изобразить однозначно заданную плоскость;
4. через любую точку, находящуюся в 3D-пространстве и не расположенную на заданной прямой, возможно провести лишь одну прямую, что параллельна заданной.

Рассмотрим подробнее лемму про параллельные прямые и докажем ее. К примеру, некая прямая (b) пересекает плоскость (∝) в точке (M) , что расположена на заданной плоскости. Параллельные прямые a и образуют некую плоскость (β) . Таким образом, если точка (M) общая для плоскостей (∝) и (β) , то эти плоскости пересекаются, линию пересечения обозначим c, на ней расположена точка (M) .
Все прямые (a) , (b) и (c) расположены в плоскости (β) .

Не нашли что искали?

Просто напиши и мы поможем

В соответствии с аксиомой планиметрии, при пересечении одной из параллельных прямых третьей прямой, вторая так же будет ее пересекать.

В нашем варианте прямая a пересекает прямую c в точке (K) .

Точка (K) расположена одновременно на прямой a и на плоскости (∝) , значит она есть общей для них. Таким образом, прямая a пересекает плоскость (∝) .

Пример задачи о параллельных прямых

Заданы прямые (a) и (b) , описывающиеся уравнениями. Определить, параллельны ли заданные прямые.
(a: == ) ;

При совпадении прямых или если они параллельны их направляющие векторы (s_1) и ( s_2) будут коллинеарными, таким образом, их координаты будут иметь следующее соотношение:

Для того, чтобы найти направляющие вектора, воспользуемся каноническими уравнениями, таким образом для прямой a вектор (s_1) будет равен .

Для прямой b найдем направляющий вектор при помощи произведения нормальных векторов плоскостей, на которых он расположен:

Таким образом, соблюдается вышеуказанное условие, значит эти прямые либо параллельны, либо совпадают. Необходимо определить каковыми именно они являются: параллельны или совпадают. Возьмем некую точку (K) с координатами (1;2;-1), находящуюся на прямой a, и подставим ее координаты в уравнение прямой (b) :
1-2+1+1=0;1=0,

Равенство не выполняется, таким образом, точка (K) не расположена на прямой (b) , а это означает, что прямые (a) и (b) не совпадают, соответственно они параллельны.

Взаимное расположение двух прямых в пространстве.
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Признак скрещивающихся прямых

Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся прямые		Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.
Две параллельные прямые		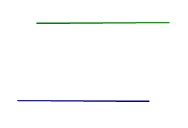Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек
Две скрещивающиеся прямые		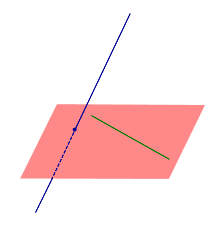Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

Две пересекающиеся прямые

Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две параллельные прямые

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две скрещивающиеся прямые

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.

Фигура	Рисунок	Тип утверждения и формулировка
Две различные точки		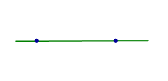Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия.
Прямая линия и точка, не лежащая на этой прямой		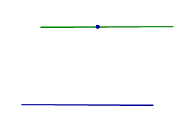Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.
Две пересекающиеся прямые		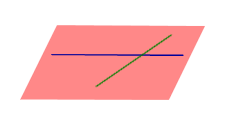Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Две параллельные прямые		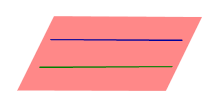Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две различные точки

Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Прямая линия и точка, не лежащая на этой прямой

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Две пересекающиеся прямые

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две параллельные прямые

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Признак скрещивающихся прямых

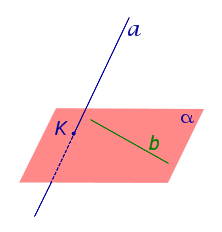
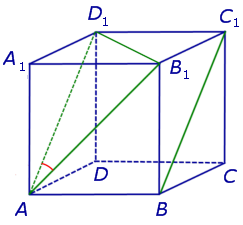
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».

Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.

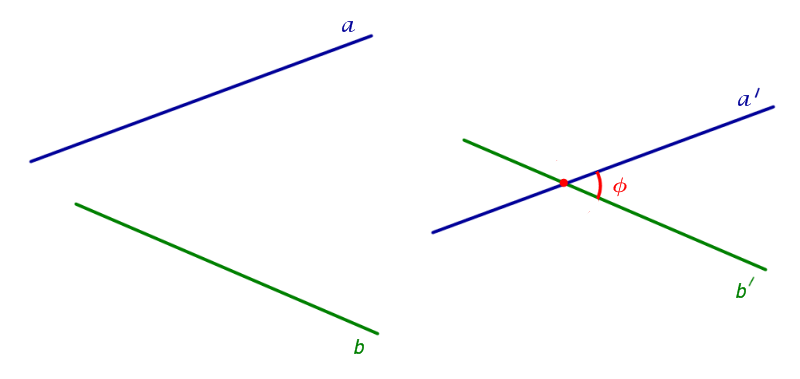
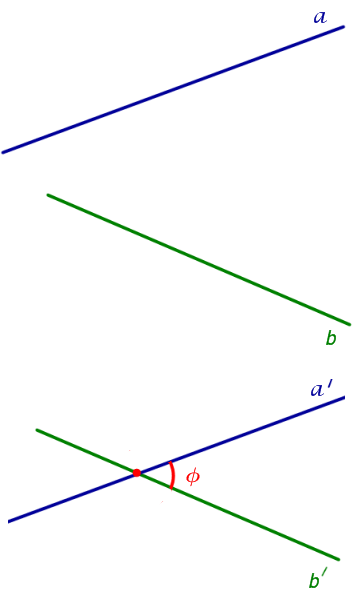
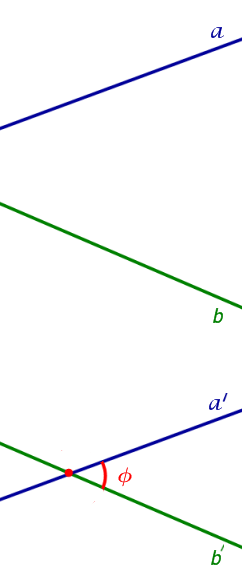
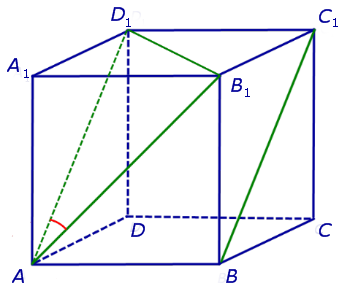
Угол между скрещивающимися прямыми

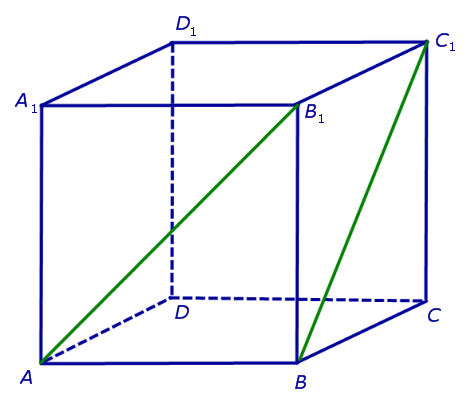
На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .

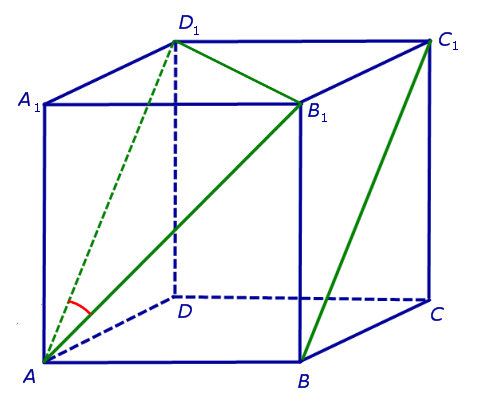
Для того, чтобы найти угол между прямыми AB₁ и BC₁ , проведем в кубе диагональ боковой грани AD₁ и диагональ верхнего основания D₁B₁ (рис. 4).

Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».

Параллельные прямые в пространстве. Параллельность трех прямых

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы дадим основные определения и теоремы на тему параллельных прямых в пространстве.
В начале урока рассмотрим определение параллельных прямых в пространстве и докажем теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной. Далее докажем лемму о двух параллельных прямых, пересекающих плоскость. И с ее помощью докажем теорему о двух прямых, параллельных третьей прямой.

🔥 Видео