Если в четырехугольнике противоположные углы попарно равны то его противоположные

Доказательство:

Дано: АВСD — четырехугольник, АD = ВС, АDВС.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

2. Рассмотрим АВС и АDС: АС — общая, 1 =3 (т.к. по условию АDВС, 1 и 3 накрест лежащие углы при пересечении параллельных прямых АD и BC секущей АС), АВС =АDС (по 1 признаку равенства треугольников), АВ = DC и 2 = 4. Но 2 и 4 накрест лежащие углы при пересечении прямых АВ и DС секущей АС, АВDС.

3. Итак, АDВС и АВDС, т.е. в четырехугольнике АВСD противоположные стороны попарно параллельны, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Доказательство:

Дано: АВСD — четырехугольник, АВ = DС, АD = ВC.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

2. Рассмотрим АВС и АDС: АС — общая, по условию АВ = DС, АD = ВC, АВС =АDС (по 3 признаку равенства треугольников), 1 = 2, при этом 1 и 2 накрест лежащие при пересечении прямых АD и ВC секущей АС, по признаку параллельности двух прямых АDВС.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Доказательство:

Дано: АВСD — четырехугольник, АС и DВ диагонали, АС ∩ DВ = О, АО = ОС, DО = ОВ.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Рассмотрим АОD и ВОС: по условию АО = ОС, DО = ОВ, АОD и ВОС (как вертикальные углы), АОD =ВОС (по 1 признаку равенства треугольников), АD = ВC и 1 = 2.

2. 1 и 2 накрест лежащие при пересечении прямых АD и ВC секущей АС, при этом 1 = 2, по признаку параллельности двух прямых АDВС.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Видео:В параллелограмме противоположные углы равны 8кл теоремаСкачать

Параллелограмм

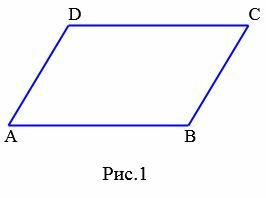
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.

На Рис.1 изображен параллелограмм поскольку ( small AB || CD, ;; AD || BC .)

Видео:№430. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположныеСкачать

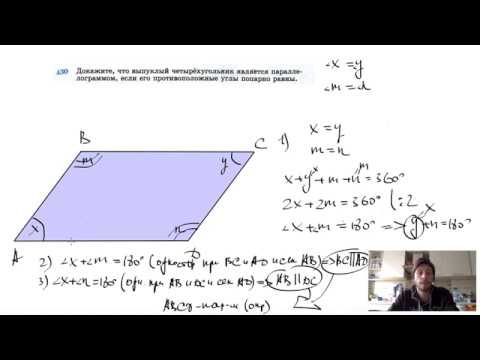
Свойства параллелограмма

Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).

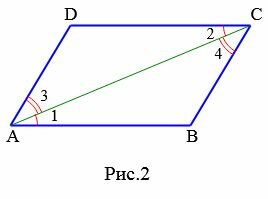Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. ( small angle 1=angle 2 ) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично ( small angle 3=angle 4 ), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, ( small angle 1=angle 2 ), ( small angle 3=angle 4 ) (см. статью Треугольники. Признаки равенства треугольников). Поэтому ( small AB=CD, ;; AD=BC, ;; angle B=angle D. )

Из рисунка Рис.2 имеем: ( small angle A=angle 1+angle 3, ;; angle C=angle 2+angle 4. ) Учитывая, что ( small angle 1=angle 2 ) и ( small angle 3=angle 4 ), получим: ( small angle A=angle C. )

Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.

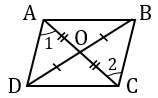
Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. ( small angle 1=angle 2 ) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. ( small angle 3=angle 4 ), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам. Тогда AO=OC и BO=OD.

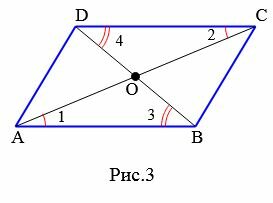Видео:8 класс, 4 урок, ПараллелограммСкачать

Признаки параллелограмма

Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.

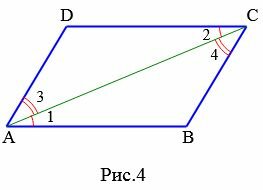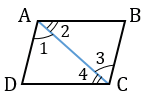
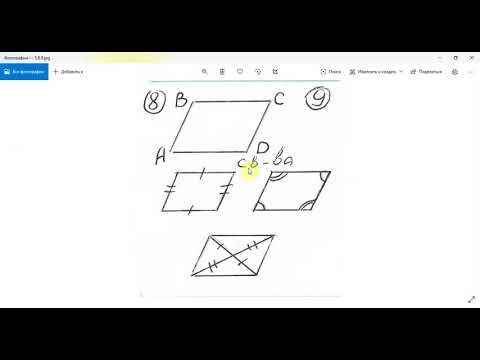
Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то ( small angle 1=angle 2 ) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона ( small angle 1=angle 2 ). Но тогда ( small angle 3=angle 4. ) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку ( small angle 3 ) и ( small angle 4 ) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм.

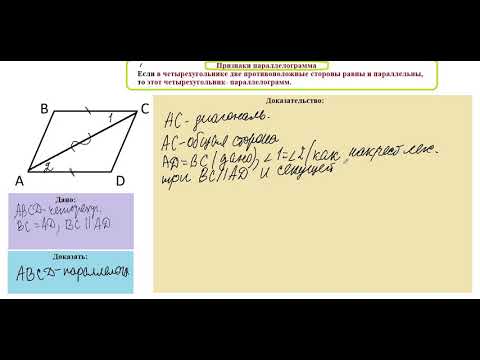
Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.

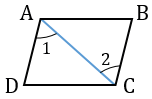
Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда ( small angle 1=angle 2 ). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.

Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.

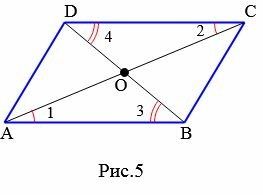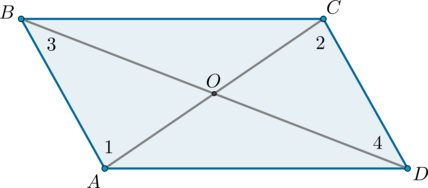
Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:

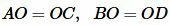Углы AOB и COD вертикальные, следовательно ( small angle AOB=angle COD ). Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:

,

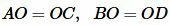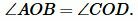Тогда AB = CD и ( small angle 1=angle 2 ). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:

и, по признаку 1 четырехугольник ABCD − параллелограмм.

Видео:Геометрия Признак параллелограмма: Если в четырехугольнике противолежащие стороны равныСкачать

Параллелограмм

Определение

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Теорема (первый признак параллелограмма)

Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

Доказательство

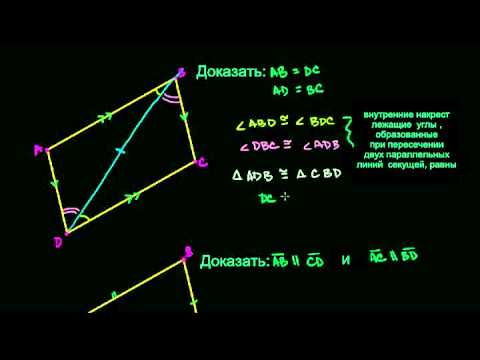
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD) .

Проведём диагональ (AC) , разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA) . Эти треугольники равны по двум сторонам и углу между ними ( (AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC) ), поэтому (angle 3 = angle 4) . Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC) , следовательно, (ADparallel BC) . Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.

Теорема (второй признак параллелограмма)

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

Доказательство

Проведём диагональ (AC) данного четырехугольника (ABCD) , разделяющую его на треугольники (ABC) и (CDA) .

Эти треугольники равны по трем сторонам ( (AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC) . Отсюда следует, что (ABparallel CD) . Так как (AB = CD) и (ABparallel CD) , то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.

Теорема (третий признак параллелограмма)

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Доказательство

Рассмотрим четырехугольник (ABCD) , в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.

Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ( (AO = OC) , (BO = OD) по условию, (angle AOB = angle COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle 2) . Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC) ) следует, что (ABparallel CD) .

Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.

Свойства параллелограмма:

1. В параллелограмме противоположные стороны равны и противоположные углы равны.

2. Диагонали параллелограмма точкой пересечения делятся пополам.

Свойства биссектрисы параллелограмма:

1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.

2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.

3. Отрезки биссектрис противоположных углов равны и параллельны.

Доказательство

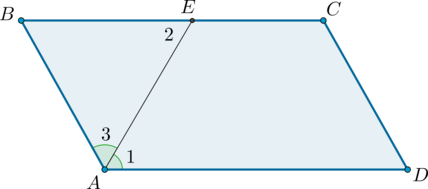
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD) .

Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE) . Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2) , откуда следует, что треугольник (ABE) – равнобедренный.

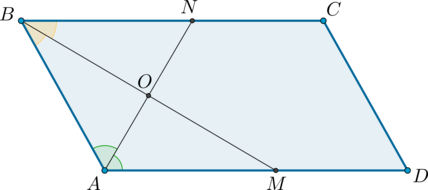
2) Пусть (ABCD) – параллелограмм, (AN) и (BM) – биссектрисы углов (BAD) и (ABC) соответственно.

Так как сумма односторонних углов при параллельных прямых и секущей равна (180^) , тогда (angle DAB + angle ABC = 180^) .

Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM = 0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^) , откуда (angle AOB = 180^circ — (angle BAN + angle ABM) = 90^circ) .

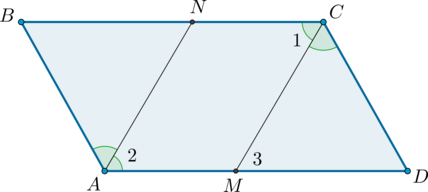
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD) .

Так как в параллелограмме противоположные углы равны, то (angle 2 = 0,5cdotangle BAD = 0,5cdotangle BCD = angle 1) . Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM) , тогда (angle 2 = angle 3) , откуда следует, что (ANparallel CM) . Кроме того, (AMparallel CN) , тогда (ANCM) – параллелограмм, следовательно, (AN = CM) .

📸 Видео

Геометрия Признак параллелограмма: Если в четырех угольнике каждые две противолежащие стороны равныСкачать

8 класс, 5 урок, Признаки параллелограммаСкачать

Признак параллелограмма (если в четырехугольнике две стороны равны и параллельны, тоСкачать

Противоположные стороны параллелограмма равны 8 клСкачать

Признаки параллелограмма. Геометрия 8 класс. Глава 5Скачать

Какой четырехугольник называется параллелограммом? Геометрия 8 класс. Глава 5Скачать

№ 430 - Геометрия 7-9 класс АтанасянСкачать

Противолежащие стороны параллелограмма равныСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Признак параллелограмма (второй), 8 классСкачать

8 класс. Геометрия. Четырехугольник: вершины, стороны, диагонали. Свойства параллелограмма. Урок #1Скачать

Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать

ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

🤠 Техас: выстрел АВРОРЫ! Шатун Штатов. Бортник: Три месяца Газы. Фронт горит! Броня ТЦК. Запрет УПЦСкачать