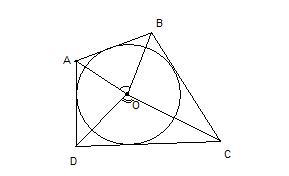
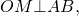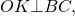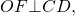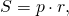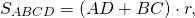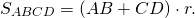Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.
На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.
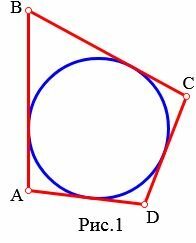 |
Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.
Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).
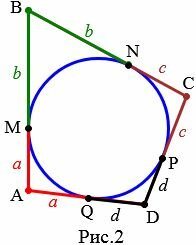 |
Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то
| ( small AM=AQ=a, ) ( small BM=BN=b, ) ( small CN=CP=c, ) ( small DQ=DP=d ) |
| ( small AB+CD ) ( small=AM+BM+CP+DP ) ( small =a+b+c+d, ) | (1) |
| ( small AD+BC) ( small=AQ+DQ+BN+CN) ( small=a+d+b+c. ) | (2) |
Из равенств (1) и (2), следует:
( small AB+CD=AD+BC. )  |
Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.
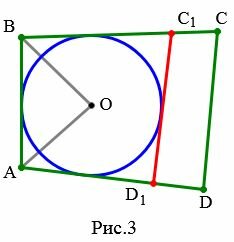 |
Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.
Пусть эта окружность не касается стороны CD. Тогда возможны два случая.
Случай 1. Сторона CD не имеет общих точек с построенной окружностью.
Проведем касательную C1D1 к окружности, параллельно стороне CD четырехугольника.
Тогда окружность с центром O вписан в четырехугольник ABC1D1. Следовательно, по теореме 1, имеем:
| ( small AB+C_1D_1=AD_1+BC_1. ) | (3) |
Но по условию данной теоремы:
| ( small AB+CD=AD+BC. ) | (4) |
Вычтем из равенства (4) равенство (3):
| ( small CD-C_1D_1) (small=AD-AD_1+BC-BC_1 ) |
| ( small CD-C_1D_1=DD_1+CC_1 ) |
| ( small CD=DD_1+CC_1+C_1D_1) |
Получили, что в четырехугольнике CC1D1D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).
Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.
Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).
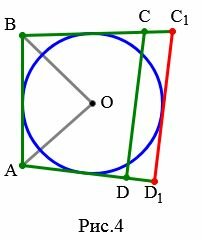 |
Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.
Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.
- Вписанная в четырехугольник окружность
- Докажите, что если в четырехугольник АВСД вписана окружность с центром в точке О, то угол АОВ + угол СОД = 180 градусов?
- Четырехугольник АВСД вписан в окружность?
- Четырехугольник АВСД вписан в окружность?
- В угол С велечиной 79 градусов вписана окружность с центром О которая касается сторон угла в точках А и В?
- Чему равен угол угол АДС четырехугольника АВСД, вписанного в окружность, если угол АСД = 32 градуса, СВД = 56 градусов, САВ = 48 градусов?
- В угол с величиной 99 градусов вписана окружность с центром в точке О, которая касается сторон угла в точках А и В?
- В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности?
- В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности?
- В угол с величиной 75° вписана окружность которая касается сторон угла в точках А и В где о — центр окружность?
- Треугольник ABC вписан в окружность с центром в точке О Найдите ACB если угол АОВ равен 173 градуса?
- Точка О — центр вписанной в треугольник АВС окружности найти угол С , если угол АОВ равен 128 градусам?
- 🎦 Видео
Видео:3 правила для вписанного четырехугольника #shortsСкачать

Вписанная в четырехугольник окружность
Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.
Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.

И обратно, если суммы противоположных сторон четырехугольника равны:
то в четырехугольник ABCD можно вписать окружность.
Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.

AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,
то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.
3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.

5. Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
где p — полупериметр четырехугольника.
Так как суммы противолежащих сторон описанного четырехугольника равны, полупериметр равен любой из пар сумм противолежащих сторон.
Например, для четырехугольника ABCD p=AD+BC или p=AB+CD и
Соответственно, радиус вписанной в четырехугольник окружности равен
Видео:Если в четырёхугольник можно вписать окружностьСкачать

Докажите, что если в четырехугольник АВСД вписана окружность с центром в точке О, то угол АОВ + угол СОД = 180 градусов?
Геометрия | 5 — 9 классы
Докажите, что если в четырехугольник АВСД вписана окружность с центром в точке О, то угол АОВ + угол СОД = 180 градусов.
Рассмотрим треугольник АОВ.
Здесь < ; OAB = 1 / 2< ; A.
Для этого утверждения мы использовали свойство касательных к окружности : отрезки касательных АВ и АD к окружности, проведенные из одной точки А, равны и составляют равные углы с прямой АО, проходящей через эту точку А и центр окружности О (< ; OAB = < ; OAD = 1 / 2< ; A).
Таким же образом утверждаем, что< ; ОВА = 1 / 2< ; В (касательные ВС и ВА проведены к окружности из точки В).
Зная сумму углов треугольника, запишем :
< ; AOB = 180 — (< ; OAB + < ; OBA) = 180 — (1 / 2< ; A + 1 / 2< ; B) = 180 — 1 / 2(< ; A + < ; B).
Рассмотрим треугольник COD.
Здесь < ; OCD = 1 / 2< ; C (касательные CB и CD к окружности проведены из точки С) и < ; ODC = 1 / 2< ; D (касательные DC и DA проведены из точки D).
< ; COD = 180 — (< ; OCD + < ; ODC) = 180 — (< ; 1 / 2< ; C + 1 / 2< ; D) = 180 — 1 / 2(< ; C + < ; D).
Зная сумму углов четырехугольника ABCD, запишем :
< ; A + < ; B + < ; C + < ; D = 360,
< ; A + < ; B = 360 — < ; C — < ; D.
В выражение < ; AOB = 180 — 1 / 2(< ; A + < ; B) подставим значение для суммы < ; A + < ; B :
< ; AOB = 180 — 1 / 2(< ; A + < ; B) = 180 — 1 / 2(360 — < ; C — < ; D) = 1 / 2(< ; C + < ; D).
Запишем сумму углов АОВ и COD :
< ; AOB + < ; COD = 1 / 2(< ; C + < ; D) + 180 — 1 / 2(< ; C + < ; D) = 180°, что и требовалось доказать.
Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Четырехугольник АВСД вписан в окружность?
Четырехугольник АВСД вписан в окружность.
Угол АВС равен 48 градусов, угол САД равен 38 градусов.
Найдите угол АВД.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Четырехугольник АВСД вписан в окружность?
Четырехугольник АВСД вписан в окружность.
Угол Авс равен 130 градусов, угол САД равен79 град.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

В угол С велечиной 79 градусов вписана окружность с центром О которая касается сторон угла в точках А и В?
В угол С велечиной 79 градусов вписана окружность с центром О которая касается сторон угла в точках А и В.
Найдиде угол АОВ.
Видео:В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать

Чему равен угол угол АДС четырехугольника АВСД, вписанного в окружность, если угол АСД = 32 градуса, СВД = 56 градусов, САВ = 48 градусов?
Чему равен угол угол АДС четырехугольника АВСД, вписанного в окружность, если угол АСД = 32 градуса, СВД = 56 градусов, САВ = 48 градусов.
Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

В угол с величиной 99 градусов вписана окружность с центром в точке О, которая касается сторон угла в точках А и В?
В угол с величиной 99 градусов вписана окружность с центром в точке О, которая касается сторон угла в точках А и В.
Найдите угол АОВ.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности?
В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности.
Найдите угол АОВ.
Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности?
В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности.
Найдите угол АОВ.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В угол с величиной 75° вписана окружность которая касается сторон угла в точках А и В где о — центр окружность?
В угол с величиной 75° вписана окружность которая касается сторон угла в точках А и В где о — центр окружность.
Найти угол АОВ ответ дать в градусах.
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Треугольник ABC вписан в окружность с центром в точке О Найдите ACB если угол АОВ равен 173 градуса?
Треугольник ABC вписан в окружность с центром в точке О Найдите ACB если угол АОВ равен 173 градуса.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Точка О — центр вписанной в треугольник АВС окружности найти угол С , если угол АОВ равен 128 градусам?
Точка О — центр вписанной в треугольник АВС окружности найти угол С , если угол АОВ равен 128 градусам.
Вы перешли к вопросу Докажите, что если в четырехугольник АВСД вписана окружность с центром в точке О, то угол АОВ + угол СОД = 180 градусов?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
1. Площадь ромба — это половина произведения его диагоналей. То есть S = 10 * 16 / 2 = 80 см квадратных. 2. По теореме Пифагора c = Так как сторона, лежащая против угла 30 градусов равна половине гипотенузы (пускай это будет сторона а), то формула..
Находим углы треугольника АВС = X + x + 90 = 180 2x = 180 — 90 X = 90 : 2 X = 45 Это значит что трейгольник АВС равнобедреный Треугольник МЛКтоже равнобедреный = >треугольники равны по стороне и двум прележащим к ней углам = >что соответствующие элем..
Ответ : 14Пошаговое объяснение : CD = BD — BCCD = 27 + x — (3x + 47) = 27 + x — 3x — 47 = — 2x — 20CE = CD + DE = — 2x — 20 + 10 = — 2x — 10С другой стороны, СЕ = х + 26, x + 26 = — 2x — 103x = — 36x = — 12CE = x + 26 = — 12 + 26 = 14.
Решение в приложении.
ЕН⊥СН и EF⊥CF. Углы между соответственно перпендикулярными прямыми равны, значит∠FCH = ∠FEH. ВЕ = CF, значит ЕBCF — прямоугольник. BF — диагональ. Точка О — центр описанной окружности около прямоугольника. ∠FCH = ∠FEH значит FH — хорда окружност..
По теореме Пифагора 100 — 73 = 27. Сторона треугольника равна 2 корень из 27, или 6 корень из 3. Треугольник равносторонний. Расстояние от данной точки до плоскости треугольника — расстояние от точки до точки пересечения биссектрис (высот, медиан)..
16 — (5×2) = 6 6÷2 = 3 Друга сторона паралелограма 3см.
Sтрап. = ½(17 + 9)×4 = 13×4 = 52см².
12) С 16) А 17) D 18) С.
180 — 90 — 70 = 20 180 — (20 * 2) = 140 — один угол 180 — 140 = 40 — другой угол.
🎦 Видео
Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

11 класс, 44 урок, Описанный четырехугольникСкачать

Задание 26 Вписанный четырёхугольникСкачать
Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Тема 9. Вписанные и описанные четырехугольникиСкачать

Геометрия 11 класс. Вписанный четырехугольникСкачать