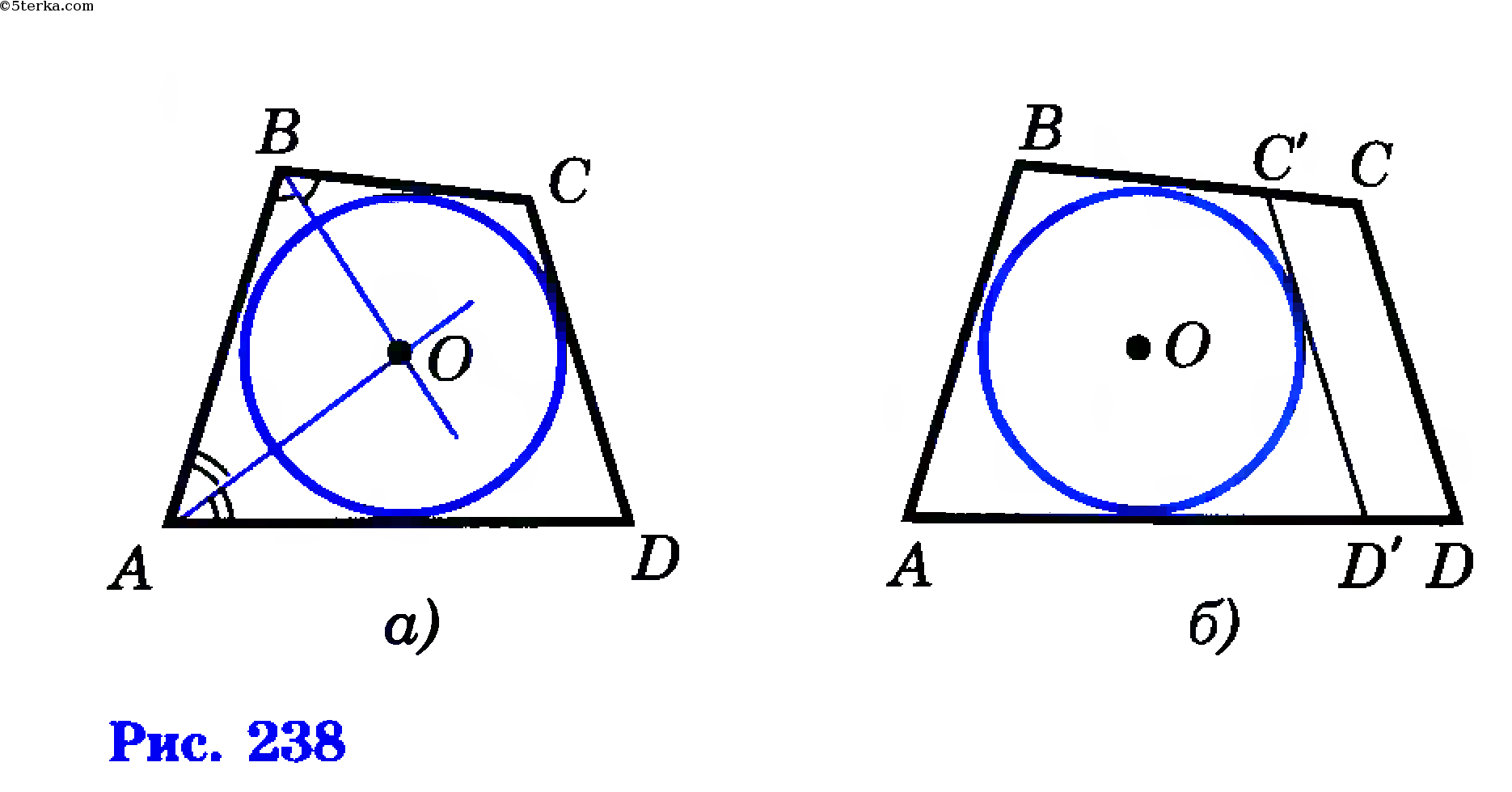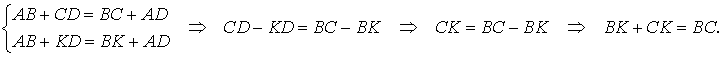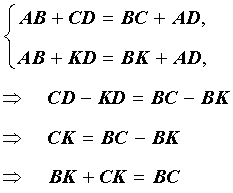Если суммы противоположных сторон выпуклого четырехугольника равны то в него можно вписать (6 видео)

724 Докажите, что если в выпуклом четырехугольнике суммы противоположных сторон равны, то в этот четырехугольник можно вписать окружность.

Пусть в выпуклом четырехугольнике ABCD

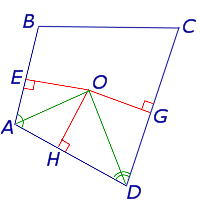
Точка О пересечения биссектрис углов А и В равноудалена от сторон AD, АВ и ВС, поэтому можно провести окружность с центром О, касающуюся указанных трех сторон (рис. 238, а). Докажем, что эта окружность касается также стороны CD и, значит, является вписанной в четырехугольник ABCD.

Предположим, что это не так. Тогда прямая CD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай (рис. 238, б). Проведем касательную C’D’, параллельную стороне CD (С’ и D’ — точки пересечения касательной со сторонами ВС и AD). Так как ABC’D’ — описанный четырехугольник, то по свойству его сторон

Но ВС’ =ВС -С’С, AD’ =AD — D’D, поэтому из равенства (2) получаем:

Правая часть этого равенства в силу (1) равна CD. Таким образом, приходим к равенству

т.е. в четырехугольнике C’CDD’ одна сторона равна сумме трех других сторон. Но этого не может быть, и, значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны CD, что и требовалось доказать.

Решебник по геометрии за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №724
к главе «Глава VIII. Окружность. Дополнительные задачи».

Содержание

Вписанная окружность
Доказательство
Доказательство
Доказательство
Доказательство
Доказательство
Доказательство
Описанные четырехугольники
💡 Видео

Видео:№430. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположныеСкачать

Вписанная окружность

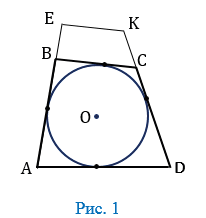
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность. На рисунке 1 четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

Теорема

В любой треугольник можно вписать окружность.

Доказательство

Дано: произвольный АВС.

Доказать: в АВС можно вписать окружность.

Доказательство:

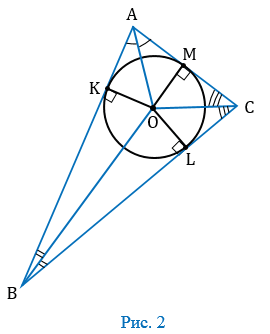
1. Проведем биссектрисы углов А, В и С, которые пересекутся в точке О (следствие из свойства биссектрис). Из точки О проведем перпендикуляры ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА (Рис. 2).

2. Точка О равноудалена от сторон АВС (свойство биссектрис), поэтому ОК = ОL = ОМ. Следовательно, окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны АВС касаются этой окружности в точках К, L, М, т.к. они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в АВС. Теорема доказана.

Замечание 1

В треугольник можно вписать только одну окружность.

Доказательство

Предположим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают, значит в треугольник можно вписать только одну окружность. Что и требовалось доказать.

Замечание 2

Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности.

Доказательство

На рисунке 2 мы видим, что АВС составлен из трех треугольников: АВО, ВСО и САО. Пусть АВ, ВС и АС основания треугольников АВО, ВСО и САО соответственно, тогда высотами данных треугольников окажутся отрезки ОК = ОL = ОМ = r ( r — радиус окружности с центром О). Следовательно, площади этих треугольников вычисляются по формулам: . Тогда, по свойству площадей, площадь треугольника АВС выражается формулой: , где — периметр АВС. Что и требовалось доказать.

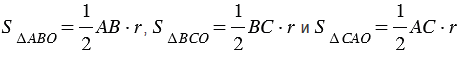
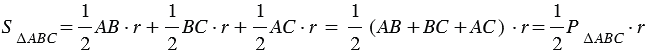
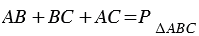
Замечание 3

Не во всякий четырехугольник можно вписать окружность.

Доказательство

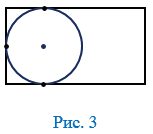
Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т.е. прямоугольник, не являющийся квадратом. В такой прямоугольник можно «поместить» окружность, касающуюся трех его сторон (Рис.3), но нельзя «поместить» окружность так, чтобы она касалась всех четырех его сторон, т.к. диаметр окружности меньше большей стороны прямоугольника т.е. нельзя вписать окружность. Что и требовалось доказать.

Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:

В любом описанном четырехугольнике суммы противоположных сторон равны.

Доказательство

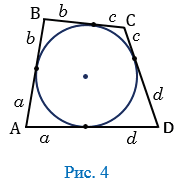
Рассмотрим четырехугольник АВСD, описанный около окружности (Рис. 4).

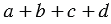
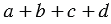
На рисунке 4 одинаковыми буквами обозначены равные отрезки касательных, т.к. отрезки касательных к окружности, проведенные из одной точки, равны. Тогда АВ + СD = и ВС + АD = , следовательно, АВ + СD = ВС + АD.

Верно и обратное утверждение:

Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Доказательство

Пусть в выпуклом четырехугольнике АВСD

АВ + СD = ВС + АD. (1)

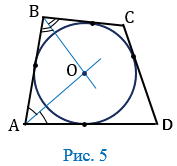
Точка О пересечения биссектрис углов А и В равноудалена от сторон АD, АВ и ВС (свойство биссектрис), поэтому можно провести окружность с центром О, касающуюся указанных трех сторон (Рис. 5).

Докажем, что эта окружность касается также стороны СD и, значит, является вписанной в четырехугольник АВСD.

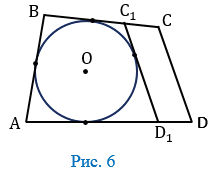
Предположим, что это не так. Тогда прямая СD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай (Рис. 6). Проведем касательную С₁D₁, параллельную стороне СD (С₁ и D₁ — точки пересечения касательной со сторонами ВС и АD).

Так как АВС₁D₁ — описанный четырехугольник, то по свойству его противоположных сторон

АВ + С₁D₁ = ВС₁ + AD₁. (2)

Но ВС₁ = ВС — С₁С, АD₁ = АD — D₁D, поэтому из равенства (2) получаем:

С₁D₁ + С₁С + D₁D = ВС + АD — АВ.

Правая часть этого равенства в силу (1) равна СD. Следовательно, приходим к равенству

т.е. в четырехугольник С₁СDD₁ одна сторона равна сумме трех других сторон. Но этого не может быть, т.к. к аждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон. Значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны СD. Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Видео:Геометрия Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можноСкачать

Описанные четырехугольники

Определение 1 . Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником .

Замечание . В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.

Теорема 1 . Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.

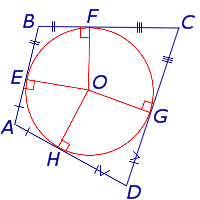
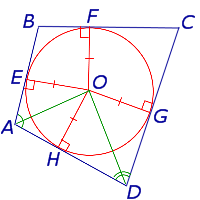
Доказательство . Рассмотрим четырёхугольник ABCD , описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).

AH = AE, BF = BE, CF = CG, DH = DG,

Складывая эти равенства, получим:

AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,

то справедливо равенство

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

Доказательство . Рассмотрим четырёхугольник ABCD , длины сторон которого удовлетворяют равенству

и проведём биссектрисы углов BAD и CDA . Обозначим точку пересечения этих биссектрис буквой O , и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).

Следовательно, справедливы равенства

из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH , касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:

Окружность касается касается стороны BC (рис.4).

В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.

Окружность не касается стороны BC .

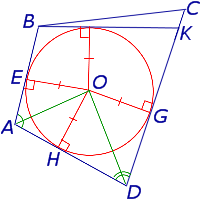
В этом случае касательная, проведенная к окружности из точки B , пересекает прямую DC в точке K , и возможны два случая:

Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:

Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольника неравенству треугольника неравенству треугольника . Полученное противоречие доказывает, что случай 2а невозможен.

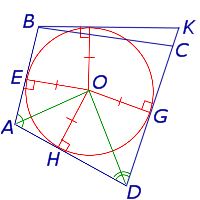
Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.

Итак, возможен и реализуется лишь случай 1.

Из доказательства теоремы 2 непосредственно вытекает

Теорема 3 . Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.

В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.

Примеры описанных четырёхугольников

Фигура	Рисунок	Утверждение
Ромб		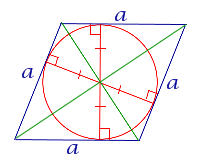В любой ромб можно вписать окружность
Квадрат		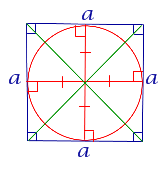В любой квадрат можно вписать окружность
Прямоугольник		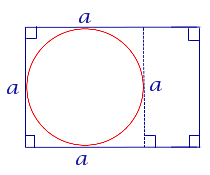В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом
Параллелограмм		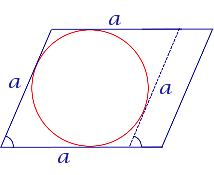В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом
Дельтоид		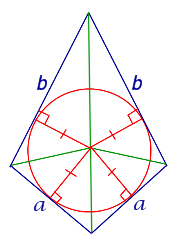В любой дельтоид можно вписать окружность
Трапеция		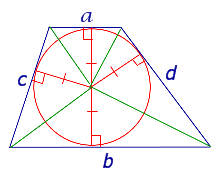В трапецию можно вписать окружность тогда и только тогда, когда у трапеции *сумма длин боковых сторон рана сумме длин оснований*