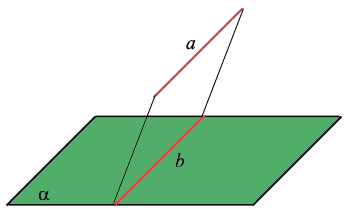
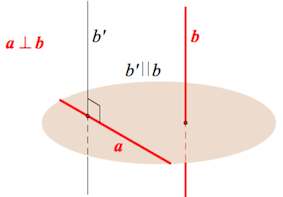
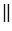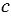Если прямая перпендикулярна плоскости то она параллельна какой нибудь прямой этой плоскости (5 видео)

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

Две плоскости называются параллельными, если они не пересекаются.

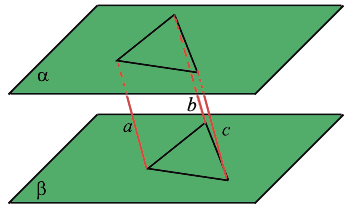
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как

Отрезки параллельных прямых между параллельными плоскостями равны.

= =

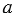
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

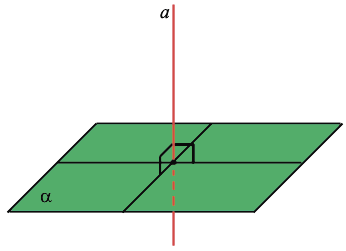
Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.

Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.

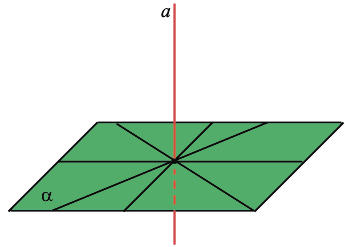
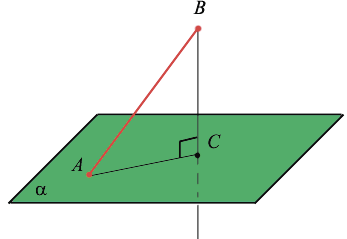
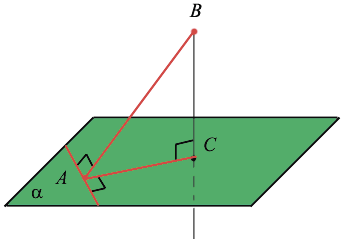
Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

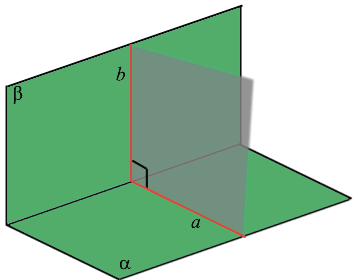
Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.

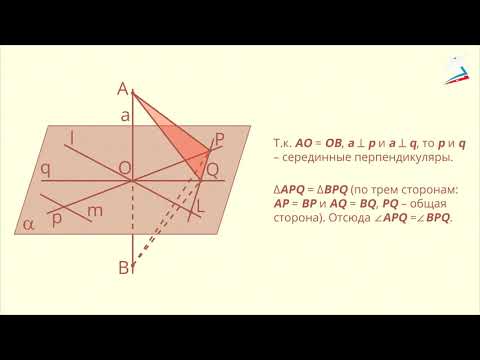
Так как , то .

Поделись с друзьями в социальных сетях:

Содержание

Перпендикулярность прямых и плоскостей
Перпендикулярные прямые
Перпендикулярность прямой и плоскости
Признак перпендикулярности прямой и плоскости
Свойства перпендикулярных прямой и плоскости
Перпендикулярность плоскостей
Признак перпендикулярности плоскостей
Свойство перпендикулярных плоскостей
Параллельность прямой и плоскости
💡 Видео

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Перпендикулярность прямых и плоскостей

Видео:10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

Перпендикулярные прямые

Две прямые в пространстве называются перпендикулярными , если угол между ними составляет .

При этом прямые могут пересекаться,

а могут быть скрещивающимися:

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Перпендикулярность прямой и плоскости

Прямая называется перпендикулярной к плоскости , если она перпендикулярна любой прямой, лежащей в этой плоскости.

Признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Свойства перпендикулярных прямой и плоскости

1). Две прямые, перпендикулярные одной и той же плоскости, параллельны.

2). Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.

3). Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой

Видео:Геометрия 10 класс (Урок№8 - Перпендикулярность прямой и плоскости.)Скачать

Перпендикулярность плоскостей

Пересекающиеся плоскости называются перпендикулярными , если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Признак перпендикулярности плоскостей

Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Свойство перпендикулярных плоскостей

Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямой и плоскости

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок посвящен теме «Параллельность прямой и плоскости». На этом уроке мы обсудим параллельность прямой и плоскости как один из трех возможных вариантов их взаимного расположения в пространстве, рассмотрим ситуацию плоскость параллельная прямой. Сформулируем теорему и докажем ее и два утверждения, которые часто используются при решении задач на эту тему.