Признак параллельности прямой и плоскости
Все возможные случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Формулировка | |||||||||||
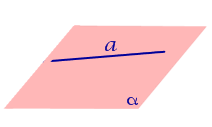
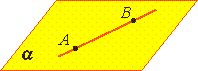
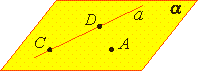
| Прямая лежит на плоскости (принадлежит плоскости) |  | ||||||||||||
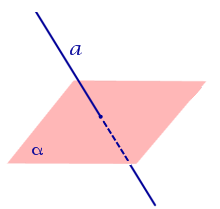
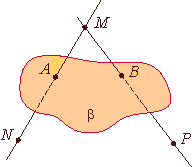
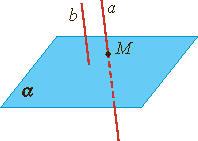
| Прямая пересекает плоскость | 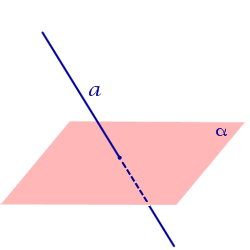 | ||||||||||||
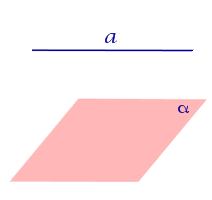
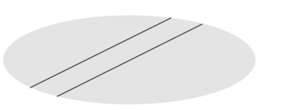
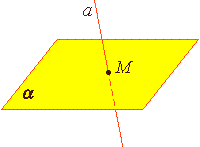
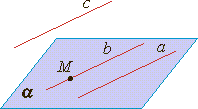
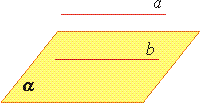
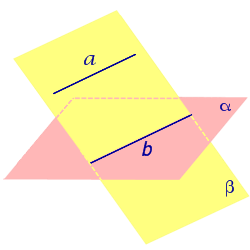
| Прямая параллельна плоскости | 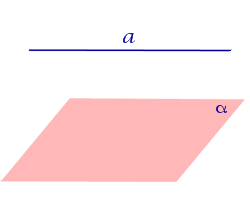 |
| Прямая лежит на плоскости (принадлежит плоскости) | |
| Прямая пересекает плоскость | |
| Прямая параллельна плоскости | |
 |
 |
| Рис.1 |
 |
| Рис.2 |
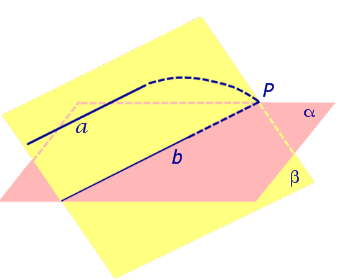
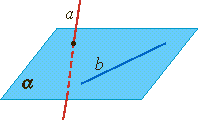
Доказательство . Рассмотрим случай 2 и предположим противное. Предположим, что прямые a и b пересекаются в некоторой точке P (рис.3) .
Но тогда точка P оказывается точкой пересечения прямой a и плоскости α , и мы получаем противоречие с тем, что прямая a и плоскость α параллельны. Полученное противоречие и завершает доказательство утверждения 1.
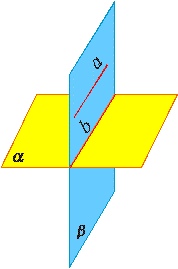
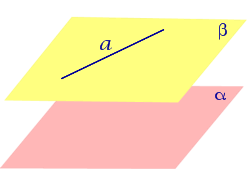
Утверждение 2 (признак параллельности прямой и плоскости) . Если прямая a , не лежащая в плоскости α , параллельна некоторой прямой b , лежащей в плоскости α , то прямая a и плоскость α параллельны.
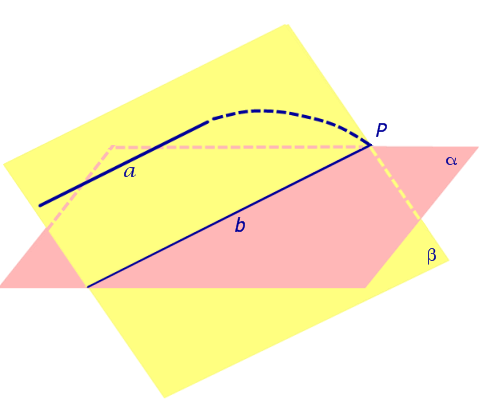
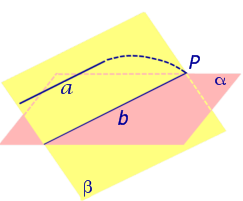
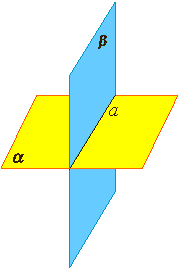
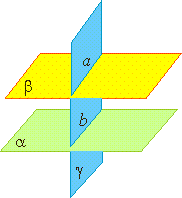
Доказательство. Докажем признак параллельности прямой и плоскости «от противного». Предположим, что прямая a пересекает плоскость α в некоторой точке P . Проведем плоскость β через параллельные прямые a и b Проведем плоскость β через параллельные прямые a и b (рис. 4).
Точка P лежит на прямой a и принадлежит плоскости β. Но по предположению точка P принадлежит и плоскости α , следовательно точка P лежит на прямой b , по которой пересекаются плоскости α и β . Однако прямые a и b параллельны по условию и не могут иметь общих точек.
Полученное противоречие завершает доказательство признака параллельности прямой и плоскости.
- Параллельность прямых и плоскостей
- Параллельные прямые
- Признак параллельности прямых
- Параллельные прямая и плоскость
- Признак параллельности прямой и плоскости
- Свойство прямой, параллельной данной плоскости
- Параллельные плоскости
- Признаки параллельности плоскостей
- Свойства параллельных плоскостей
- Если прямая и плоскость имеют две общие точки то они пересекаются параллельны
- 10 класс
- Аксиомы стереометрии и их следствия
- Некоторые следствия из аксиом
- Параллельные прямые в пространстве
- 📺 Видео
Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Параллельность прямых и плоскостей
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельные прямые
Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.
Признак параллельности прямых
Две прямые, параллельные третьей, параллельны между собой.
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Параллельные прямая и плоскость
Прямая и плоскость называются параллельными , если они не имеют общих точек.
Признак параллельности прямой и плоскости
Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.
Свойство прямой, параллельной данной плоскости
Если плоскость β проходит через прямую a , параллельную плоскости α , и пересекает эту плоскость по прямой b , то b || a .
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

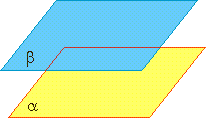
Параллельные плоскости
Параллельные плоскости – плоскости, которые не пересекаются.
Признаки параллельности плоскостей
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.
Свойства параллельных плоскостей
Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.
Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Если прямая и плоскость имеют две общие точки то они пересекаются параллельны
10 класс
Материалы к зачетной работе по теме
«Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей»
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Простейшие фигуры в пространстве: точка, прямая, плоскость.

Аксиомы стереометрии и их следствия
Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3.
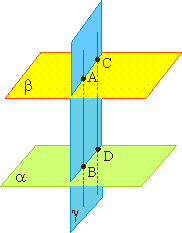
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.
Некоторые следствия из аксиом
Теорема 2.
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
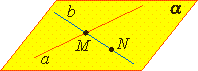
Параллельные прямые в пространстве
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Теорема о трех прямых в пространстве.
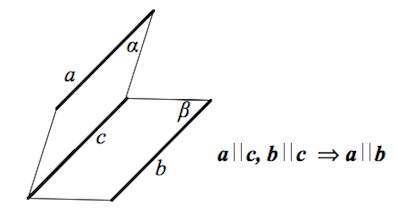
Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости
Теорема.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Теорема.
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Взаимное расположение прямых в пространстве
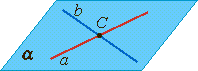 | 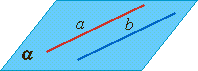 |  |
Признак параллельности двух плоскостей Теорема. | 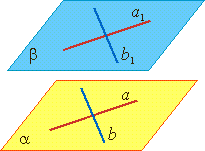 |
Свойства параллельных плоскостей
Вели α∥β и они пересекаются с γ, то а∥b.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Если α∥β и AB∥CD, то АВ = CD.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
📺 Видео
Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Параллельность прямой к плоскостиСкачать

Геометрия 10 класс Параллельность прямых, прямой и плоскости теорияСкачать

Параллельность прямых. 10 класс.Скачать

10 класс, 2 урок, Аксиомы стереометрииСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

6. Параллельность прямой и плоскостиСкачать

10 класс, 10 урок, Параллельные плоскостиСкачать

Построение точки пересечения прямой и плоскости | Стереометрия #29 | ИнфоурокСкачать

№13. Могут ли две плоскости иметь: а) только одну общую точку; б) только две общие точкиСкачать

ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ и ПЛОСКОСТИ 10 11 класс стереометрияСкачать

Точка встречи прямой с плоскостьюСкачать

ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ 10 класс стереометрияСкачать