- Вписанная окружность
- Описанная окружность
- Задачи
- Ответы к задачам
- Описанная и вписанная окружность
- теория по математике 📈 планиметрия
- Описанная окружность
- Вписанная окружность
- Вписанный и описанный треугольники
- Вписанный и описанный четырехугольники
- Многоугольник. Свойства четырехугольников описанных около окружности.
- 💥 Видео
Вписанная окружность
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности. На рисунке 231 четырёхугольник EFMN описан около окружности с центром О, а четырёхугольник DKMN не является описанным около этой окружности, так как сторона DK не касается окружности.
На рисунке 232 треугольник АВС описан около окружности с центром О.
Докажем теорему об окружности, вписанной в треугольник.
| В любой треугольник можно вписать окружность. |
Рассмотрим произвольный треугольник АВС и обозначим буквой О точку пересечения его биссектрис. Проведём из точки О перпендикуляры OK, OL и ОМ соответственно к сторонам АВ, ВС и СА (см. рис. 232). Так как точка О равноудалена от сторон треугольника АВС, то OK = OL = ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны треугольника АВС касаются этой окружности в точках К, L, М, так как они перпендикулярны к радиусам OK, OL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС. Теорема доказана.
Отметим, что в треугольник можно вписать только одну окружность.
В самом деле, допустим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудалён от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают.
Обратимся к рисунку 232. Мы видим, что треугольник АВС составлен из трёх треугольников: ABO, ВСО и САО. Если в каждом из этих треугольников принять за основание сторону треугольника АВС, то высотой окажется радиус r окружности, вписанной в треугольник АВС. Поэтому площадь S треугольника АВС выражается формулой
| площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности. |
В отличие от треугольника не во всякий четырёхугольник можно вписать окружность.
Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т. е. прямоугольник, не являющийся квадратом. Ясно, что в такой прямоугольник можно «поместить» окружность, касающуюся трёх его сторон (рис. 233, а), но нельзя «поместить» окружность так, чтобы она касалась всех четырёх его сторон, т. е. нельзя вписать окружность. Если же в четырёхугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
| В любом описанном четырёхугольнике суммы противоположных сторон равны. |
Это свойство легко установить, используя рисунок 233, б, на котором одними и теми же буквами обозначены равные отрезки касательных. В самом деле, АВ + CD = а + b + с + d, ВС + AD-a + b + c + d, поэтому АВ + CD = ВС + AD. Оказывается, верно и обратное утверждение:
| Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность (см. задачу 724). |
Описанная окружность
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник — вписанным в эту окружность. На рисунке 234 четырёхугольник ABCD вписан в окружность с центром О, а четырёхугольник AECD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.
Треугольник АВС на рисунке 235 является вписанным в окружность с центром О.
Докажем теорему об окружности, описанной около треугольника.
| Около любого треугольника можно описать окружность. |
Рассмотрим произвольный треугольник АВС. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведём отрезки ОА, ОВ и ОС (рис. 235). Так как точка О равноудалена от вершин треугольника АВС, то О А = ОВ = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника АВС. Теорема доказана.
Отметим, что около треугольника можно описать только одну окружность.
В самом деле, допустим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудалён от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают.
В отличие от треугольника около четырёхугольника не всегда можно описать окружность.
Например, нельзя описать окружность около ромба, не являющегося квадратом (объясните почему). Если же около четырёхугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
| В любом вписанном четырёхугольнике сумма противоположных углов равна 180°. |
Это свойство легко установить, если обратиться к рисунку 236 и воспользоваться теоремой о вписанном угле. В самом деле,
Оказывается, верно и обратное:
| Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность (см. задачу 729). |
Задачи
689. В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13 см. Найдите радиус окружности, вписанной в этот треугольник.
690. Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведённую к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см.
691. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см, считая от основания. Найдите периметр треугольника.
692. В треугольник АВС вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и R. Найдите АР, РВ, BQ, QC, СВ, RA, если АВ = 10 см, ВС = 12 см, СА = 5 см.
693. В прямоугольный треугольник вписана окружность радиуса г. Найдите периметр треугольника, если: а) гипотенуза равна 26 см, r = 4см; б) точка касания делит гипотенузу на отрезки, равные 5 см и 12 см.
694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенуза треугольника равна с, а сумма катетов равна m.
695. Сумма двух противоположных сторон описанного четырёхугольника равна 15 см. Найдите периметр этого четырёхугольника.
696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм — ромб.
697. Докажите, что площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
698. Сумма двух противоположных сторон описанного четырёхугольника равна 12 см, а радиус вписанной в него окружности равен 5 см. Найдите площадь четырёхугольника.
699. Сумма двух противоположных сторон описанного четырёхугольника равна 10 см, а его площадь — 12 см 2 . Найдите радиус окружности, вписанной в этот четырёхугольник.
700. Докажите, что в любой ромб можно вписать окружность.
701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждый из них впишите окружность.
702. В окружность вписан треугольник АВС так, что АВ — диаметр окружности. Найдите углы треугольника, если: а) 

703. В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найдите углы треугольника, если 
704. Окружность с центром О описана около прямоугольного треугольника. а) Докажите, что точка О — середина гипотенузы. б) Найдите стороны треугольника, если диаметр окружности равен d, а один из острых углов треугольника равен α.
705. Около прямоугольного треугольника АВС с прямым углом С описана окружность. Найдите радиус этой окружности, если: а) АС = 8 см, ВС = 6 см; б) АС = 18 см, ∠B = 30°.
706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружности равен 10 см.
707. Угол, противолежащий основанию равнобедренного треугольника, равен 120°, боковая сторона треугольника равна 8 см. Найдите диаметр окружности, описанной около этого треугольника.
708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любой равнобедренной трапеции.
709. Докажите, что если около параллелограмма можно описать окружность, то этот параллелограмм — прямоугольник.
710. Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.
711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. Для каждого из них постройте описанную окружность.
Ответы к задачам
689. 
692. АР =1,5 см, РВ = 8,5 см, BQ = 8,5 см, QC = 3,5 см, CR= 3,5 см, RА = 1,5 см.
693. а) 60 см; б) 40 см.
702. a) ∠A = 67°, ∠B = 23°, ∠C = 90°; б) ∠A = 55°, ∠B = 35°, ∠C = 90°.
703. ∠A = 51°, ∠B = ∠C = 64°30′ или ∠A= 129°, ∠B = ∠C = 25°30′.
704. 6) d, d sin α, d cos α.
705. a) 5 cm; б) 18см. Указание. Воспользоваться задачей 704.
709. Указание. Воспользоваться свойством углов вписанного четырёхугольника.
710. Указание. Воспользоваться задачей 659.
Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Описанная и вписанная окружность
теория по математике 📈 планиметрия
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Описанная окружность
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.
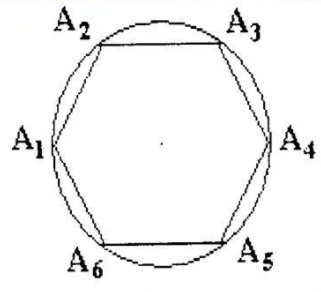
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанная окружность
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.
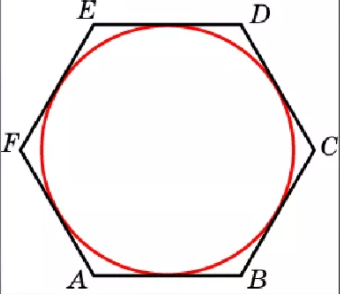
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.
Вписанный и описанный треугольники
Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
В любой треугольник можно вписать окружность: 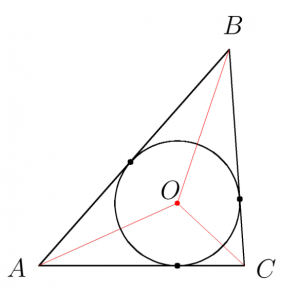
Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Вписанный и описанный четырехугольники
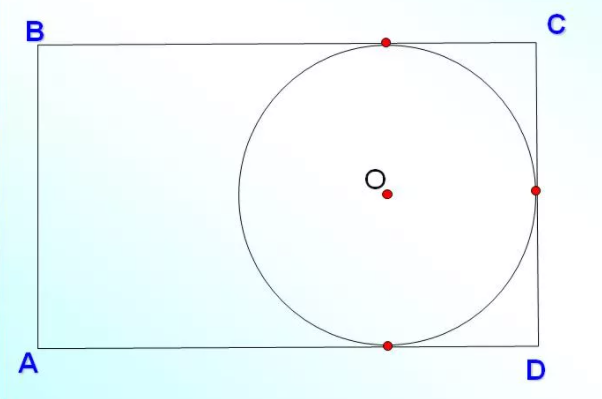
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.
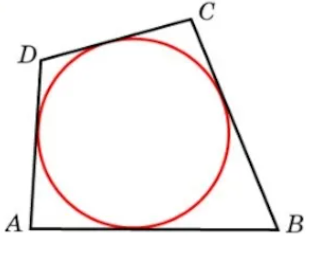
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.
На рисунке выполняется данное условие, то есть AD + BC=DC + AB
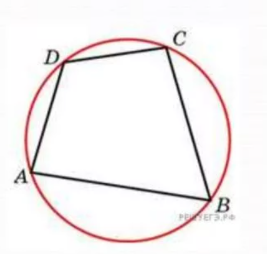
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.
На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.
Видео:Окружность касается катетовСкачать

Многоугольник. Свойства четырехугольников описанных около окружности.
Если все стороны какого-нибудь многоугольника (MNPQ) касаются окружности, то говорят, что этот многоугольник описан около окружности, или что окружность вписана в него.
Теорема.
В описанном выпуклом четырехугольнике суммы противоположных сторон равны.
Пусть ABCD будет описанный выпуклый четырехугольник, т.е. стороны его касаются окружности. Требуется доказать, что AB + CD = BC + AD.
Обратная теорема.
Если в выпуклом четырехугольнике равны суммы противоположных сторон, то в него можно вписать окружность.
Требуется доказать, что в него можно вписать окружность.
Пусть ABCD такой выпуклый четырехугольник, в котором: AB + CD = AD + BC.
💥 Видео
Окружность касается! И ВСЕХ КАСАЕТСЯ!Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Многоугольники и окружности. ЕГЭ по математике. Be Student SchoolСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

111. Окружность, вписанная в правильный многоугольникСкачать

№1084. Сколько сторон имеет правильный вписанный многоугольник, если дуга описаннойСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

78. Описанная окружностьСкачать

Вписанная окружностьСкачать

Вневписанная окружность | Теоремы об окружностях - 3Скачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Вписанная окружность. Видеоурок по геометрии 8 классСкачать