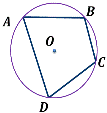
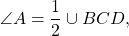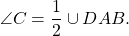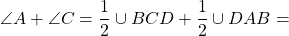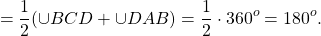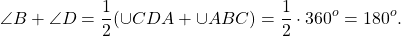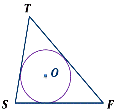Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
Поскольку четырёхугольник ABCD вписанный, сумма углов ABC и ADC равна 180°.
Получаем, что в треугольниках KAB и KCD углы ABK и CDK равны, угол K общий, следовательно, эти треугольники подобны.
Видео:Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать
Около четырехугольника можно описать окружность
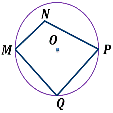
Теорема (свойство вписанного четырёхугольника)
Сумма противолежащих углов вписанного четырёхугольника равна 180°.
Дано: ABCD вписан в окр. (O; R)
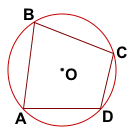
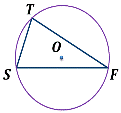
∠A — вписанный угол, опирающийся на дугу BCD.
∠C — вписанный угол, опирающийся на дугу DAB.
Так как вписанный угол равен половине дуги, на которую он опирается, то
Что и требовалось доказать.
Теорема (признак вписанного четырёхугольника)
Около четырёхугольника можно описать окружность, если сумма его противолежащих углов равна 180°.
Дано: ABCD — четырёхугольник,
Доказать: ABCD можно вписать в окружность
Опишем окружность около треугольника ABC и докажем, что точка D лежит на этой окружности.
Доказательство будем вести методом от противного.
Предположим, что точка D не лежит на описанной около треугольника ABD окружности. Тогда D лежит либо внутри этой окружности, либо вне её.
Пусть точка D лежит внутри окружности и луч AD пересекает окружность в точке E.
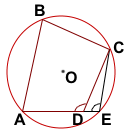
В этом случае четырёхугольник ABCE — вписанный, и сумма его противолежащих углов равна 180°: ∠B+∠E=180°.
По условию, ∠B+∠D=180°. Отсюда следует, что ∠D=∠E.
Но угол D — внешний угол треугольника DCE при вершине D.
Так как внешний угол треугольника равен сумме двух внутренних не смежных с ним углов, то
∠ADC=∠DEC+∠DCE, то есть угол D не может быть равным углу E. Пришли к противоречию. А значит, точка D не может лежать внутри окружности, описанной около треугольника ABC.
Предположим, что точка D лежит вне описанной около треугольника ABC окружности.
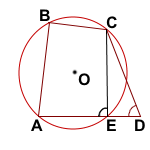
Луч AD пересекает окружность в точке E.
Тогда ABCE — вписанный четырёхугольник и ∠B+∠E=180°.
По условию, ∠B+∠D=180°. Получаем, что ∠D=∠E.
Но угол E — внешний угол треугольника ECD при вершине E. А значит,
∠AEC=∠EDC+∠DCE, то есть углы D и E не могут быть равными. Противоречие получили потому, что предположили, что точка D лежит вне окружности.
Так как точка D не может лежать внутри либо вне описанной около треугольника ABC окружности, то D лежит на этой окружности. Это значит, что около четырёхугольника ABCD можно описать окружность.
Что и требовалось доказать.
На основании свойства и признака вписанного четырёхугольника сформулируем необходимое и достаточное условие вписанного четырёхугольника.
Теорема (Необходимое и достаточное условие вписанного четырёхугольника)
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма уго противолежащих углов равна 180°.
Видео:Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть I)Скачать
Тест: Вписанная и описанная окружности
Вписанная и описанная окружности
В равнобедренном треугольнике точка касания вписанной окружности делит боковую сторону на отрезки длиной 12 см и 3 см, считая от отнования. Найдите площадь треугольника. (в ответе укажите только число без единицы измерения)
Дополните определение:
Если все стороны многоугольника касаются окружности, то окружность называется .
Если около четырехугольника можно описать окружность, то .
Выберите один из 4 вариантов ответа:
1) сумма противоположных углов равна 180 0 .
2) суммы противоположных сторон равны.
3) суммы смежных сторон равны.
4) сумма соседних углов равна 180 0 .
Какие из данных многоугольников описаны около окружности?
Выберите несколько из 3 вариантов ответа:
1) 
2) 
3) 
Найдите стороны остроугольного равнобедренного треугольника, если высота, проведенная к его основанию, равна 8 см, а радиус окружности, в которую он вписан 5 см.
Выберите несколько из 5 вариантов ответа:
1) 
2) 
Дополните определение:
Если все вершины многоугольника лежат на окружности, то окружность называется .
Окружность можно вписать в любой треугольник?
Выберите один из 5 вариантов ответа:
1) только в равносторонний.
2) в треугольник нельзя вписать окружность.
4) только в равнобедренный.
5) только в прямоугольный.
Если в четырехугольник можно вписать окружность, то .
Выберите один из 4 вариантов ответа:
1) суммы его смежных сторон равны.
2) сумма соседних углов равна 180 0 .
3) сумма противоположных углов равна 180 0 .
4) суммы его противоположных сторон равны.
Выберите верные утверждения:
Выберите несколько из 5 вариантов ответа:
1) Треугольник нельзя описать около окружности.
2) Около квадрата нельзя описать окружность.
3) Прямоугольник нельзя описать около окружности.
4) Около прямоугольника можно описать окружность.
5) Ромб можно описать около окружности.
Какие из данных многоугольников вписаны в окружность?
Выберите несколько из 3 вариантов ответа:
1) 
2) 
3) 
📸 Видео
Вписанная и описанная окружность - от bezbotvyСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать
Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать
Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать
3 правила для вписанного четырехугольника #shortsСкачать
Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать
Четырехугольники, вписанные в окружность. 9 класс.Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Геометрия Если в четырехугольнике сумма противолежащих углов равна 180, то около него можно описатьСкачать
Задание 24 ОГЭ по математике #7Скачать
Вписанная и описанная окружность в четырехугольник.Скачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать
Вписанный в окружность четырёхугольник.Скачать
