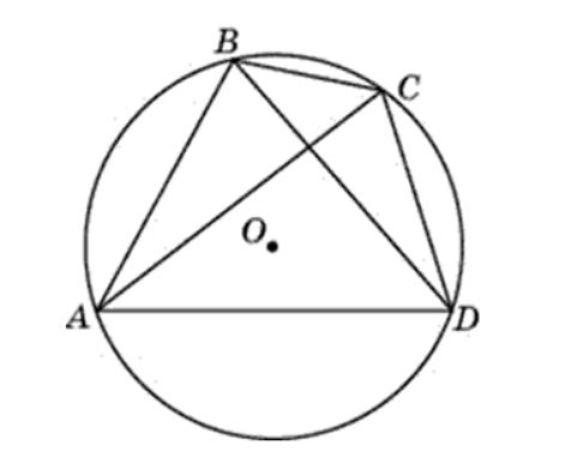
Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.
На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.
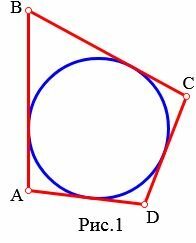 |
Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.
Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).
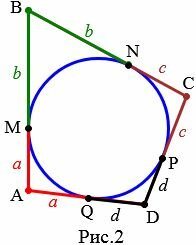 |
Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то
| ( small AM=AQ=a, ) ( small BM=BN=b, ) ( small CN=CP=c, ) ( small DQ=DP=d ) |
| ( small AB+CD ) ( small=AM+BM+CP+DP ) ( small =a+b+c+d, ) | (1) |
| ( small AD+BC) ( small=AQ+DQ+BN+CN) ( small=a+d+b+c. ) | (2) |
Из равенств (1) и (2), следует:
( small AB+CD=AD+BC. )  |
Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.
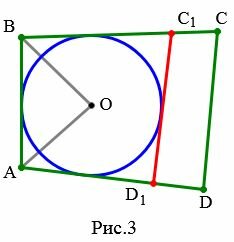 |
Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.
Пусть эта окружность не касается стороны CD. Тогда возможны два случая.
Случай 1. Сторона CD не имеет общих точек с построенной окружностью.
Проведем касательную C1D1 к окружности, параллельно стороне CD четырехугольника.
Тогда окружность с центром O вписан в четырехугольник ABC1D1. Следовательно, по теореме 1, имеем:
| ( small AB+C_1D_1=AD_1+BC_1. ) | (3) |
Но по условию данной теоремы:
| ( small AB+CD=AD+BC. ) | (4) |
Вычтем из равенства (4) равенство (3):
| ( small CD-C_1D_1) (small=AD-AD_1+BC-BC_1 ) |
| ( small CD-C_1D_1=DD_1+CC_1 ) |
| ( small CD=DD_1+CC_1+C_1D_1) |
Получили, что в четырехугольнике CC1D1D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).
Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.
Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).
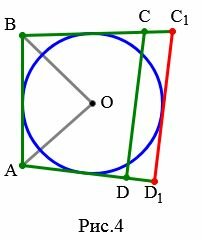 |
Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.
Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.
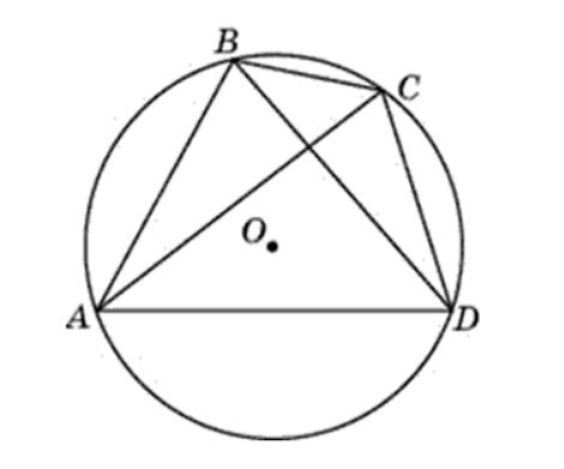
- Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность
- Общие понятия
- Частные случаи
- Свойства вписанного четырехугольника в окружность
- Теорема 1
- Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность
- Общие понятия
- Частные случаи
- Свойства вписанного четырехугольника в окружность
- Теорема 1
- 🌟 Видео
Видео:ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Угол А четырёхугольника ABCD, вписанного в окружность, равен 25.Найдите уголСкачать

Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность
С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Общие понятия
Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки.
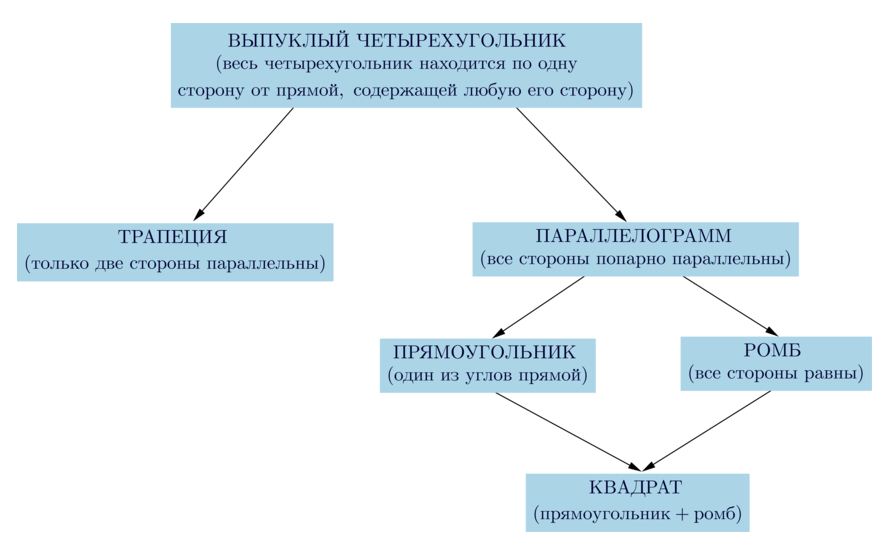
Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры.
Четырехугольник может быть следующих видов:
- Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами.
- Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет.
- Прямоугольник. Фигура, у которой все 4 угла = 90º.
- Ромб. Фигура, у которой все стороны равны.
- Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые.
Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º.
Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника.
Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Частные случаи
Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи:
- Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник.
- Если все вершины ромба находятся на описывающей линии, то он является квадратом.
- Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре.
Видео:В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать

Свойства вписанного четырехугольника в окружность
Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример.
Видео:Геометрия Сторона AD четырехугольника ABCD является диаметром окружности, описанной около негоСкачать

Теорема 1
Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º.
Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что 18 ноября, 2018
Видео:3 правила для вписанного четырехугольника #shortsСкачать

Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность
С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы.
Видео:угол a четырёхугольника abcd вписанного в окружность равен 46Скачать

Общие понятия
Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки.
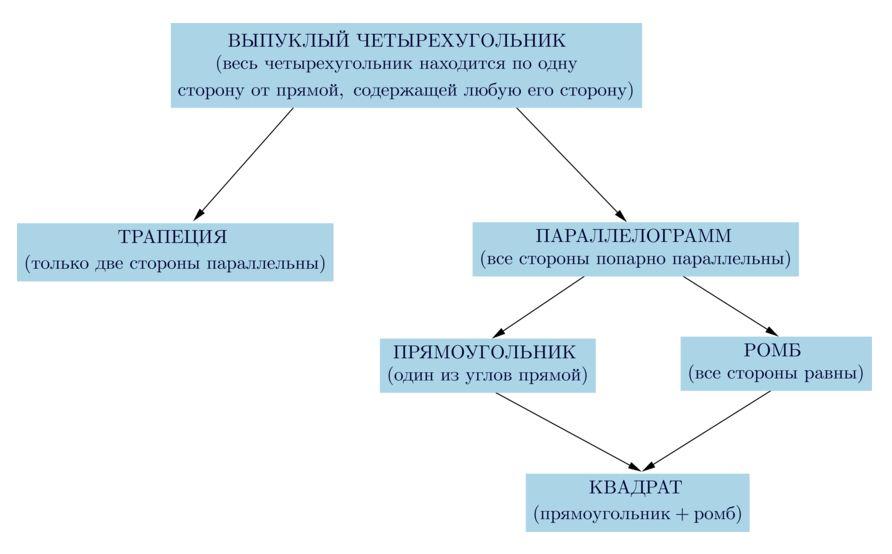
Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры.
Четырехугольник может быть следующих видов:
- Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами.
- Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет.
- Прямоугольник. Фигура, у которой все 4 угла = 90º.
- Ромб. Фигура, у которой все стороны равны.
- Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые.
Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º.
Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника.
Видео:9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

Частные случаи
Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи:
- Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник.
- Если все вершины ромба находятся на описывающей линии, то он является квадратом.
- Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре.
Видео:ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

Свойства вписанного четырехугольника в окружность
Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример.
Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Теорема 1
Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º.
Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что
🌟 Видео
Задача 6 №27876 ЕГЭ по математике. Урок 117Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

2157 углы a b c четырёхугольника ABCD относятся как 1 к 13 к 17Скачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Геометрия. ОГЭ по математике. Задание 15Скачать

В угол вписана окружность, найдите вписанный угол этой окружностиСкачать
Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

Задача на вписанную окружность ✨ #огэ #математика #егэ #геометрия #окружностьСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать