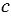Если две прямые не параллельны то они перпендикулярны верно или нет (4 видео)

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

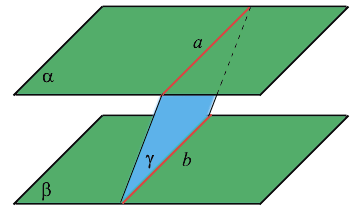
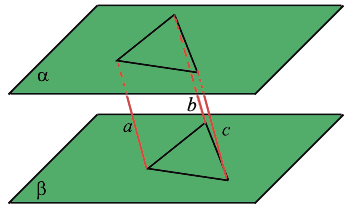
Две плоскости называются параллельными, если они не пересекаются.

Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как

Отрезки параллельных прямых между параллельными плоскостями равны.

= =

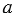
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.

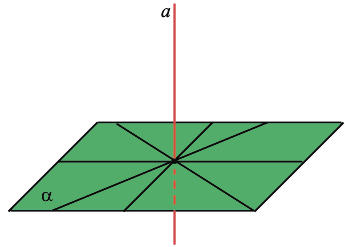
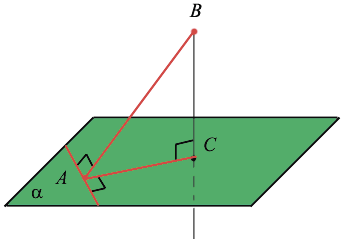
Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.

Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

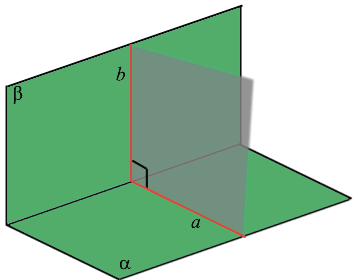
Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.

Так как , то .

Поделись с друзьями в социальных сетях:

Содержание

Если две прямые не параллельны то они перпендикулярны верно или нет
Прямая. Параллельные и перпендикулярные прямые.
теория по математике 📈 планиметрия
Обозначения прямой
Признаки параллельности прямых
Аксиома параллельных прямых
Следствия из аксиом параллельных прямых
Перпендикулярные прямые
💥 Видео

Видео:Теорема 13.2 Если две прямые параллельны третьей, то они параллельны ||Геометрия 7 класс||Скачать

Если две прямые не параллельны то они перпендикулярны верно или нет

Укажите номера верных утверждений.

1) Если угол равен 47°, то смежный с ним равен 153°.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Через любую точку проходит ровно одна прямая.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если угол равен 47°, то смежный с ним равен 153°» — неверно, сумма смежных углов равна 180°.

2) «Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны» — верно, по признаку параллельности прямых.

3) «Через любую точку проходит ровно одна прямая» — неверно через одну точку проходит бесконечное множество прямых.

Не следует думать, что вопрос «какие утверждения верные?» подразумевает, что в ответе должно быть несколько утверждений. Так же, как задача «решите уравнение» не подразумевает, что решение вообще есть.

Видео:Теорема 13.1. Две прямые, перпендикулярные третьей прямой, параллельны || Геометрия 7 класс ||Скачать

Прямая. Параллельные и перпендикулярные прямые.

теория по математике 📈 планиметрия

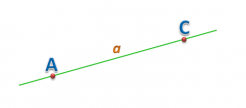
Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.

Обозначения прямой

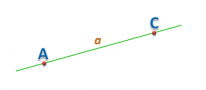
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.

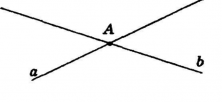
Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.

Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а ∩ b=А, где ∩ — это знак «пересечение».

Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.

Признаки параллельности прямых

Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.

Необходимо запомнить названия следующих углов:

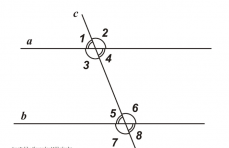
накрест лежащие углы: 4 и 5; 3 и 6;
односторонние углы: 4 и 6; 3 и 5;
соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.

С данными углами связаны следующие признаки параллельности прямых:

если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 0 , то прямые параллельны.

Видео:№123. Докажите, что если две плоскости α и β перпендикулярны к прямой а, то они параллельны.Скачать

Аксиома параллельных прямых

Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.

Через любые две точки на плоскости проходит прямая и притом только одна.

Аксиома №2 Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной.

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Следствия из аксиом параллельных прямых

Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.

Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Перпендикулярные прямые

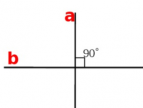
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а ⊥ b, где « ⊥ » — знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. На данном рисунке а ⟂ с, b ⟂ c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.