Перпендикуляр в произвольном треугольнике

Серединный перпендикуляр к отрезку

Окружность описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Серединный перпендикуляр к отрезку

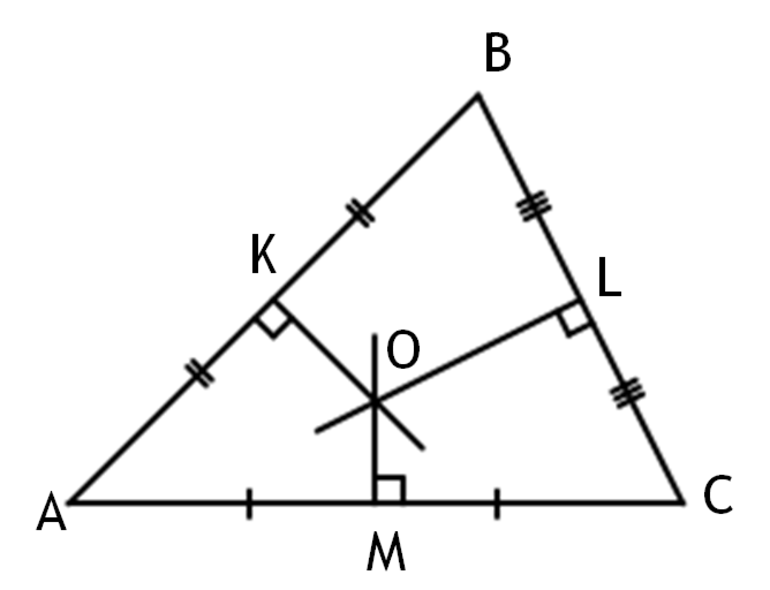
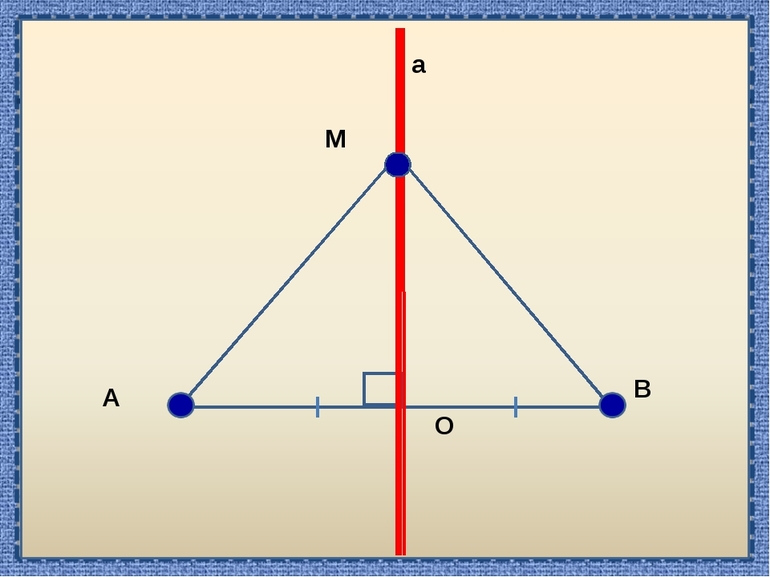
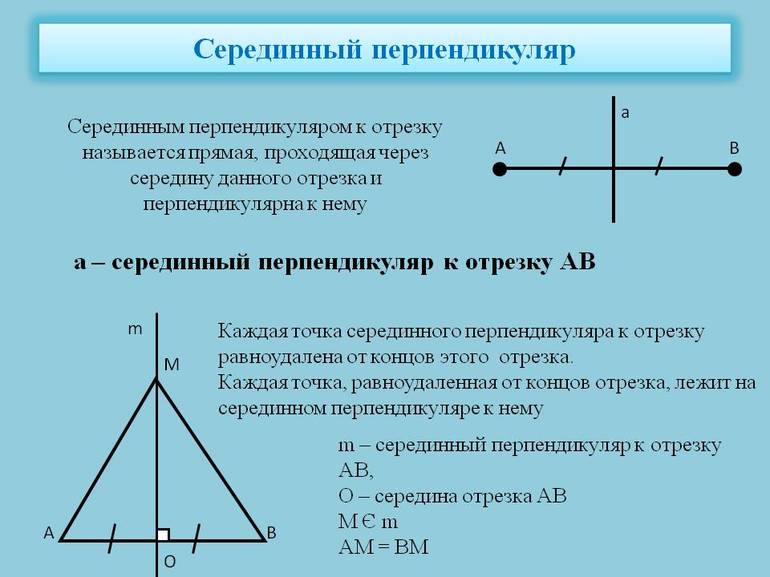
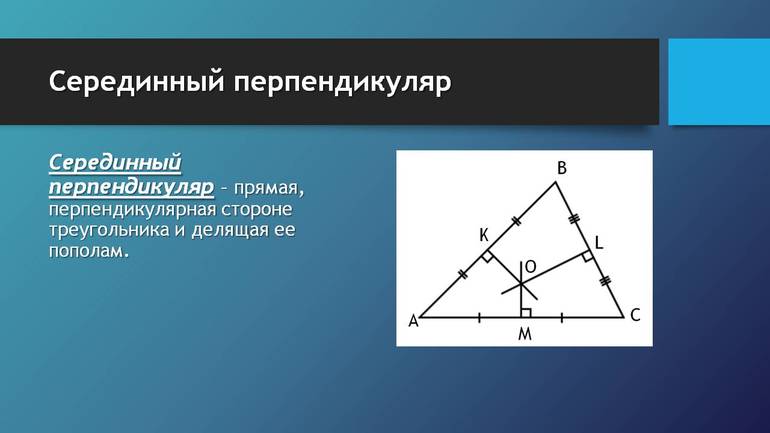
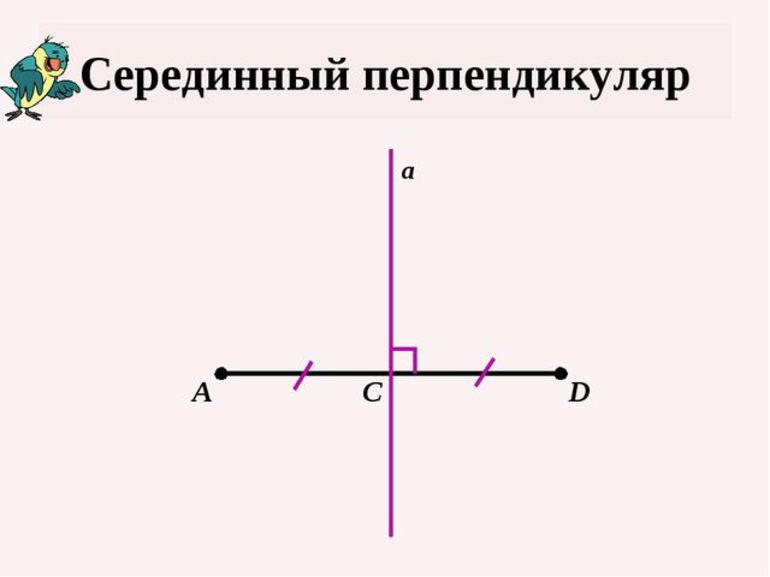
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

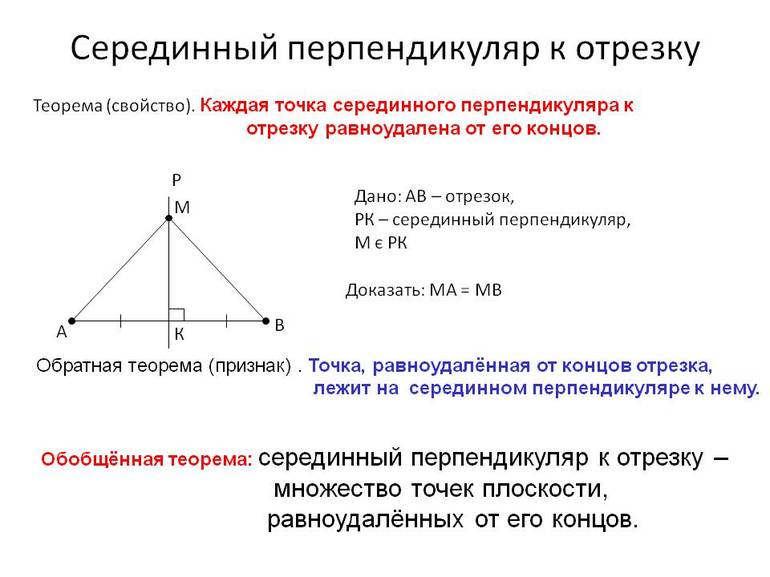
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

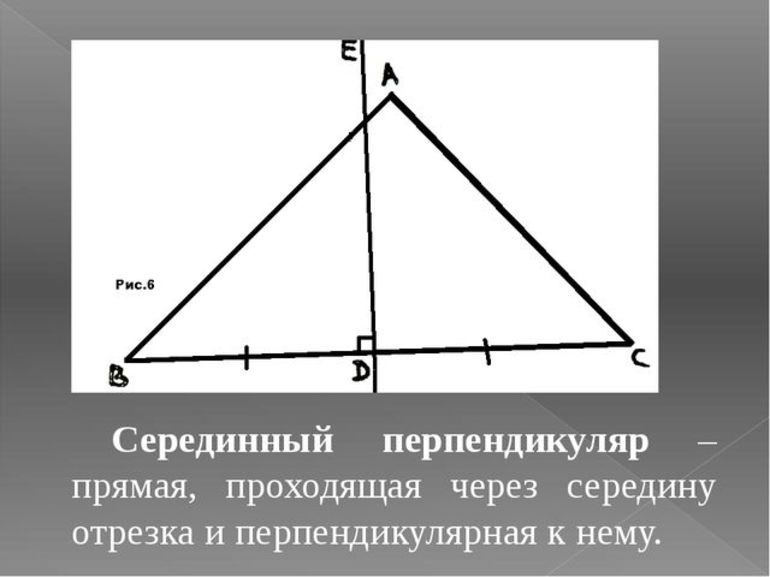
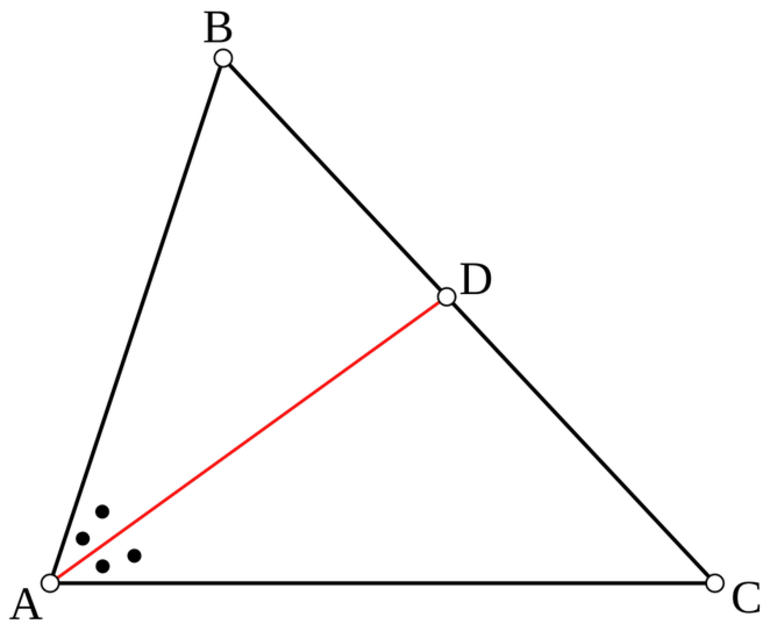
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Площадь треугольника
Радиус описанной окружности

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

l = 2Rsin φ .

(1)

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Все перпендикуляры в треугольнике

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

l = 2Rsin φ .

(1)

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Серединный перпендикуляр — определение, свойства и формулы

Общие сведения

Серединным перпендикуляром отрезка называют прямую, которая проходит под прямым углом через среднюю точку, т. е. середину отрезка. Для полного понимания материала следует остановиться на базовых элементах геометрии.

Точка — единица, при помощи которой строятся прямые, отрезки, лучи и фигуры. Прямая — простая фигура в форме бесконечной линии, состоящей из множества точек, лежащих в одной плоскости. Луч — базовая геометрическая фигура в виде бесконечной линии с одной стороны и точки-ограничителя — с другой. Иными словами, луч имеет начало, но не имеет конца. Отрезок — некоторая часть прямой (луча или другого отрезка), ограниченная двумя точками.

Кроме того, в геометрии серединный перпендикуляр встречается в треугольниках. Из определения можно сделать вывод, что им может быть прямая, отрезок и даже луч.

Аксиомы геометрии Евклида

Евклидовой геометрией называется наука о фигурах на плоскости, основанная на аксиомах и теоремах. Аксиома — базовое утверждение, не требующее доказательства. Оно используется для доказательства каких-либо теорем. Математики выделяют пять аксиом:

1. Принадлежности.
2. Порядка.
3. Конгруэнтности.
4. Параллельности прямых.
5. Непрерывности.

Формулировка первой имеет такой вид: если существует в геометрическом пространстве плоскость, состоящая из множества точек, то через любые из них можно провести только одну прямую. Иными словами, можно взять произвольные две точки и провести через них одну прямую. Чтобы начертить еще одну прямую, следует взять две другие точки.

Следующее утверждение называется аксиомой порядка. Она гласит, что существует точка, которая лежит между двумя другими на прямой. Значение слова «конгруэнтность» не совсем понятно для новичка, однако нужно постепенно привыкать к терминологии. Оно обозначает «равенство». Третий геометрический факт формулируется таким образом: когда два отрезка или угла конгруэнтны третьему, тогда они равны между собой. Аксиома касается только отрезков и углов.

Чтобы убедиться в ее правильности, нужно разобрать следующий пример: длина первого отрезка составляет 10 см, второго — тоже, а третий равен первому. Необходимо доказать, что они равны между собой. Это делается очень просто:

• Вводятся обозначения: первый — MN, второй — OP и третий — RS.
• Устанавливаются значения по условию: MN = 10 см, ОР = 10 см, а RS = MN.
• Доказательство строится таким образом: MN = RS = 10 (см). Следовательно, отрезки равны, поскольку MN = ОР = RS = 10 (см).

Следует отметить, что данные действия оказались лишними — было потрачено время на понимание простой «истины». Параллельность прямых является также аксиомой и формулируется таким образом: если существует некоторая прямая на плоскости и точка, не лежащая на ней, то через последнюю можно провести только одну параллельную ей прямую.

И последняя аксиома называется Архимедовой. Ее формулировка имеет такой вид: для произвольных отрезков, лежащих на одной прямой, существует некоторая последовательность базовых элементов (точек), лежащих на одном и другом отрезках, таких, что заданные их части равны между собой. Иными словами, на одной прямой могут быть расположены равные между собой отрезки.

Информация о треугольниках

Треугольником является любая фигура, состоящая из трех вершин (точек) соединенных отрезками (сторонами), причем точки не лежат на одной прямой в одной плоскости. Они классифицируются по такому типу:

В первом случае фигуры делятся на остроугольные, тупоугольные и прямоугольные. Остроугольным называется треугольник, у которого все углы острые (меньше 90 градусов). У тупоугольного — один угол тупой (> 90), а в прямоугольном — один из углов равен 90 градусам. Следует отметить, что сумма градусных мер углов любого треугольника эквивалентна 180.

Когда стороны у треугольника неравны между собой, тогда его называют разносторонним. При равенстве двух боковых сторон он считается равнобедренным, у которого третья сторона — основание. Если все стороны равны, то значит, фигура является равносторонней или правильной.

У треугольника есть еще и другие параметры. Их называют медианой, биссектрисой и высотой. Первый параметр является отрезком, который проводится из любой вершины на среднюю точку стороны. Высота — часть прямой, которая проводится из произвольной вершины и перпендикулярна противоположной стороне. Биссектрисой называется прямая, делящая угол на две равные части.

Медиана, высота и биссектриса, проведенные из вершины к основанию, совпадают и эквивалентны серединному перпендикуляру в треугольниках равнобедренного и равностороннего типов. Это очень важно при решении задач. Еще одним признаком, по которому выполняется классификация — подобность треугольников. У них могут быть равными только углы и некоторые стороны. Они отличаются между собой по определенному параметру, который называется коэффициентом подобия. Последний влияет только на размерность сторон. Говорят, что фигуры подобны по определенному признаку (их всего три).

Основные теоремы

Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.

Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:

• Прямая.
• Обратная.
• Пересечение в треугольнике.

Первая теорема называется прямой о СП. Она показывает, каким свойством обладают точки серединного перпендикуляра. Ее формулировка следующая: произвольная точка, которая взятая на перпендикуляре, удалена на равные расстояния от конечных точек отрезка, ограничивающих его на плоскости.

Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.

Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.

Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.

Важные свойства

Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:

1. Центр описанной окружности вокруг треугольника соответствует точке их пересечения.
2. Точка, взятая на СП, равноудалена от конечных точек отрезка и образует равнобедренный или равносторонний треугольник.
3. В треугольниках равнобедренного и равностороннего типов им является высота, медиана и биссектриса.

В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.

Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:

1. а: Pa = (2 * а * S) / (a^2 + b^2 — c^2).
2. b: Pb = (2 * b * S) / (a^2 + b^2 — c^2).
3. c: Pc = (2 * c * S) / (a^2 — b^2 + c^2).

Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:

1. Основание и высоту, проведенную к нему: S = (1/2) * a * Ha = (1/2) * b * Hb = (1/2) * c * Hc.
2. Через радиус вписанной окружности: S = (1/2) * r * (a + b + c).
3. Формулу Герона через полупериметр (р) и без него: S = [p * (p — a) * (p — b) * (p — c)]^(1/2) и S = 1/4 * [(a + b + c) * (b + c — a) * (а + c — b) * (a + b — c)]^(1/2).

В основном по таким соотношениям и нужно определить площадь. Полупериметр вычисляется таким образом: р = (а + b + с) / 2.

Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.

Пример решения задачи

В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:

1. Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
2. Серединный перпендикуляр, проведенный к диагонали прямоугольника.
3. Точка Е делит сторону на отрезки а и 2а.

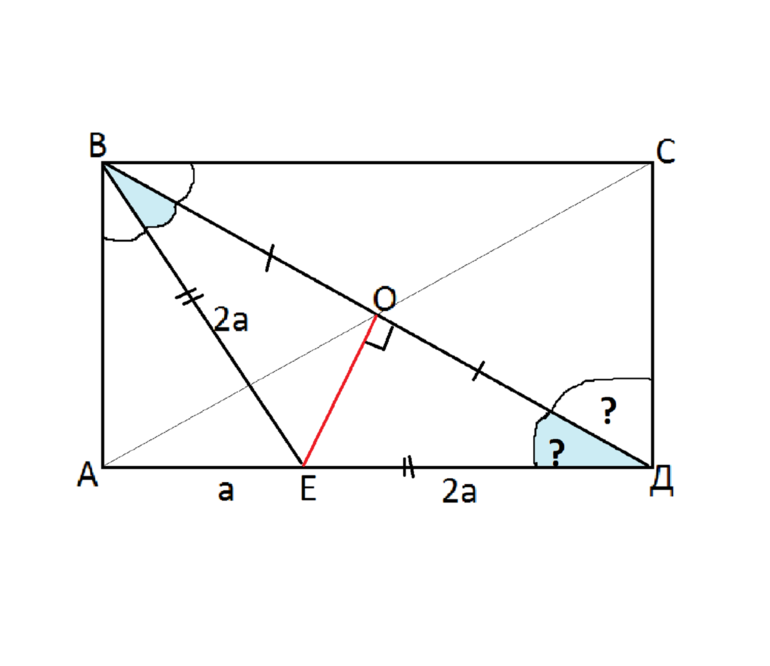
Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении

Рисунок 1. Чертеж для решения задачи.

Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:

1. Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
2. Необходимо найти угол ЕВО. Сделать это проблемно. Рекомендуется обратить внимание на треугольник АВЕ.
3. При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
4. Угол СВЕ вычисляется следующим образом: 90 — 30 = 60 (градусов).
5. Следовательно, искомый угол равен 30, поскольку 90 — 30 — 30 = 30.
6. В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).

Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой «х». Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = [4a^2 + a^2]^(1/2) = a * [5]^(1/2). Следовательно, АВ = a * [5]^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 — d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 — (d^2) / 4]^(1/2).

Таким образом, нахождение серединного перпендикуляра позволяет значительно уменьшить объемы вычислений. Однако для этого нужно знать не только основные теоремы, но и его свойства.

math4school.ru

Треугольники

Основные свойства

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.

Внешним углом треугольника называется угол, смежный внутреннему углы треугольника.

Сумма углов треугольника равна 180°:

Внешний угол равен сумме двух внутренних углов, не смежных с ним, и больше любого внутреннего, с ним не смежного:

Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол:

Средней линией треугольника называется отрезок, который соединяет середины двух его сторон.

Средняя линия треугольника параллельна одной из его сторон и равна её половине:

Равенство треугольников

Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны:

У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.)

В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны.

Первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны:

Второй признак равенства треугольников.

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны:

Третий признак равенства треугольников.

Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны:

Подобие треугольников

Подобными называются треугольники, у которых соответствующие стороны пропорциональны.

Коэффициент пропорциональности называется коэффициентом подобия:

Два треугольника подобны, если:

• Два угла одного треугольника равны двум углам другого треугольника.
• Две стороны одного треугольника пропорциональны двум сторонам другого, и углы, образованные этими сторонами, равны.
• Стороны одного треугольника пропорциональны сторонам другого.

У подобных треугольников соответствующие углы равны, а соответствующие отрезки пропорциональны:

Отношение периметров подобных треугольников равно коэффициенту подобия.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Прямая, пересекающая две стороны треугольника, и параллельная третьей, отсекает треугольник, подобный данному:

Три средние линии треугольника делят его на четыре равных треугольника, подобные данному, с коэффициентом подобия ½:

Медианы треугольника

Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Три медианы треугольника пересекаются в одной точке, делящей медианы в отношении 2:1, считая от вершины:

• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника.
• Три медианы треугольника делят его на шесть равновеликих треугольников:

Длины медиан, проведённых к соответствующим сторонам треугольника, равны:

Биссектрисы треугольника

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.

Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник.

Биссектриса внутреннего угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:

Длина биссектрисы угла А :

Биссектрисы внутреннего и смежного с ним внешнего угла перпендикулярны.

Биссектриса внешнего угла треугольника делит (внешне) противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

BL – биссектриса угла В ;

ВЕ – биссектриса внешнего угла СВК :

Высоты треугольника

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.

Высоты треугольника обратно пропорциональны его сторонам:

Длина высоты, проведённой к стороне а :

Серединные перпендикуляры

Серединный перпендикуляр – это прямая, которая проходит через середину стороны треугольника перпендикулярно к ней.

Три серединных перпендикуляра треугольника пересекаются в одной точке, которая является центром окружности, описанной около данного треугольника.

Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром противолежащей стороны лежит на окружности, описанной около данного треугольника.

Окружность, вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех его сторон.

Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков:

Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника:

Окружность, описанная около треугольника

Окружность называется описанной около треугольника, если она проходит через все его вершины.

Радиус описанной окружности:

Расположение центра описанной окружности

Центр описанной окружности остроугольного треугольника расположен внутри треугольника.Центр описанной окружности прямоугольного треугольника совпадает с серединой его гипотенузы.Центр описанной окружности тупоугольного треугольника расположен вне треугольника.

Равнобедренный треугольник

Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.

В равнобедренном треугольнике углы при основании равны: ∠ A = ∠ C.

В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой: BL – медиана, биссектриса, высота.

Основные формулы для равнобедренного треугольника:

Равносторонний треугольник

Треугольник у которого все стороны равны называется равносторонним или правильным треугольником.

Центры вписанной и описанной окружностей правильного треугольника совпадают.

Все углы равностороннего треугольника равны:

Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой, которые проведены из той же вершины:

Основные соотношения для элементов равностороннего треугольника

Прямоугольный треугольник

Треугольник называется прямоугольным, если у него есть прямой угол.

Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Прямоугольные треугольники равны если у них равны:

• два катета;
• катет и гипотенуза;
• катет и прилежащий острый угол;
• катет и противолежащий острый угол;
• гипотенуза и острый угол.

• одному острому углу;
• из пропорциональности двух катетов;
• из пропорциональности катета и гипотенузы.

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, может быть определена через катеты и их проекции на гипотенузу:

Медиана, проведённая из вершины прямого угла, равна половине гипотенузы:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит данный треугольник на два треугольника, подобные данному:

Площадь прямоугольного треугольника можно определить

через катеты:

через катет и острый угол:

через гипотенузу и острый угол:

Центр описанной окружности совпадает с серединой гипотенузы.

Радиус описанной окружности:

Радиус вписанной окружности:

Вневписанные окружности

Три окружности, каждая из которых касается одной стороны (снаружи) и продолжений двух других сторон треугольника, называются вневписанными.

Центр вневписанной окружности лежит не пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах.

Так точка О₁ , центр одной из вневписанных окружностей Δ ABC , лежит на пересечении биссектрисы ∠ A треугольника ABC и биссектрис BО₁ и C О₁ внешних углов Δ ABC при вершинах B и C .

Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырёх точках – центрах вписанной и трёх вневписанных окружностей.

Δ ABC является ортоцентричным в Δ О₁О₂О₃ (точки A , B и C – основания высот в Δ О₁О₂О₃ ).

В Δ ABC углы равны 180°–2 О₁ , 180°–2 О₂ , 180°–2 О₃ .

Радиус окружности, описанной около Δ О₁О₂О₃ , равен 2 R , где R – радиус окружности, описанной около Δ ABC .

Δ ABC имеет наименьший периметр среди всех треугольников, вписанных в Δ О₁О₂О₃ .

Если r_a , r_b , r_с – радиусы вневписанных окружностей в Δ ABC , то в Δ ABC верно:

для r –

для R –

для S –

для самих r_a , r_b , r_с –

Теоремы синусов, косинусов, тангенсов; формулы Мольвейде

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

• если c 2 > a 2 +b 2 , то угол γ – тупой ( cos γ
• если c 2 2 +b 2 , то угол γ – острый ( cos γ > 0 );
• если c 2 = a 2 +b 2 , то угол γ – прямой ( cos γ = 0 ).

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:

Теорема тангенсов (формула Региомонтана):

Как построить высоту треугольника — основные способы

С применением циркуля

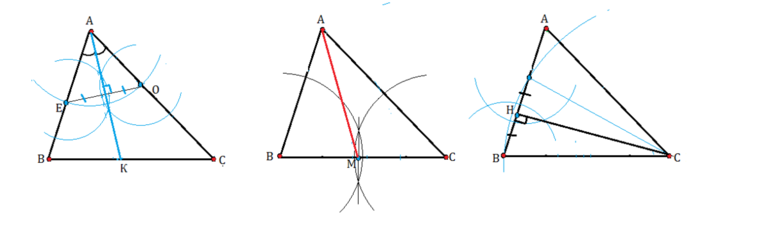
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.

Способ начертить искомый отрезок:

• На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
• Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
• Иглу циркуля ставят в вершине любого угла у основания.
• Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
• Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
• Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
• Делают пометку в месте пересечения начерченных окружностей.
• Ластиком стирают лишние линии, оставляя лишь поставленную точку.
• С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
• Стирают линии, находящиеся под основанием.

Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.

С помощью линейки

Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.

В остроугольном треугольнике

Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.

Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.

Правильная последовательность действий:

• Находят вершину, из которой хотят провести перпендикуляр.
• Совмещают угольник с противоположной стороной фигуры.
• Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
• Простым карандашом проводят линию, которая и будет искомым отрезком.

В тупоугольной фигуре

Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.

Порядок действий:

• Располагают чертёж так, чтобы тупой угол оказался у основания.
• Угольник прикладывают к наибольшей стороне фигуры.
• Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
• Соединяют 2 точки простым карандашом, получая искомую линию.

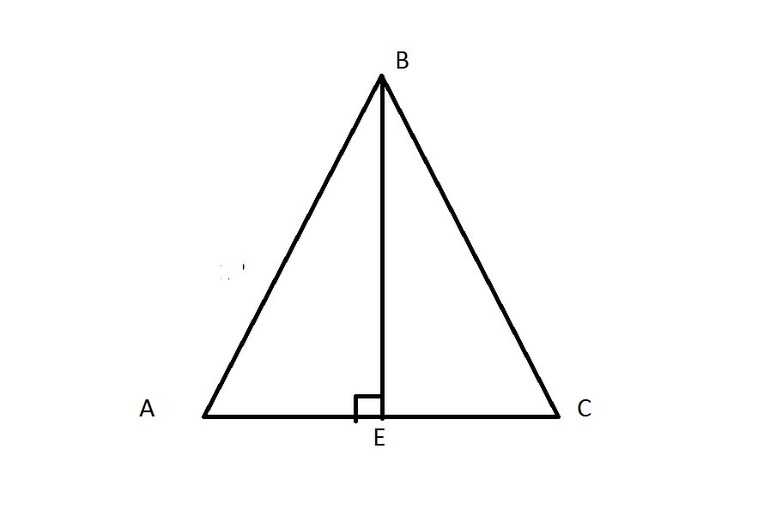
В прямоугольном и равнобедренном

В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.

Пошаговая инструкция:

• Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
• Вторую сторону линейки совмещают с вершиной прямого угла.
• Проводят линию, которая будет высотой.

Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.

Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:

• Линейкой замеряют длину основания.
• Эту величину делят на 2.
• Полученное значение откладывают от вершины одного из углов при основании.
• Отмечают середину стороны и соединяют её с верхней точкой фигуры.

Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.

Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.