Если дуга окружности составляет 80 то центральный угол 40

Геометрия | 5 — 9 классы

Если дуга окружности Составляет 80°, то центральный угол, опирающийся на эту же дугу, равен 40°.

Нет, всегда угол будет равен душе на которую он опирается, то есть 80.

Величина центрального кута равнодуге на которую он опирается.

На этой странице находится вопрос Если дуга окружности Составляет 80°, то центральный угол, опирающийся на эту же дугу, равен 40°?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

РЕШЕНИЕ СМОТРИ НА ФОТОГРАФИИ.

Биссектриса KE, проведенная из вершины острого угла прямоугольного треугольника KPT( угол P = 90) к катету PT, Делит катет в отношении 5 : 13. Найдите косинус угла KTP.

2. ∠ABN = 180° — ∠CBK — ∠KBN = 180 — 30 — 50 = 100° ∠ABM = 1 / 2 * ∠ABN = 100 : 2 = 50° — ОТВЕТ С. 6. ∠AOC = ∠BOD — как накрестлежащие в пересекающихся прямых. ТреугольникиΔAOC иΔDOBравны по двум углам и стороне. CA = BD = 10 см — ОТВЕТ.

180 — 80 = 100 180 — 50 = 130 Ответ 130 100.

Решение задания смотри на фотографии.

ΔDNR — прямоугольный, т. К. ND — высота, ∠DRN = 30°⇒по теореме DN = 1 / 2 * NR⇒NR = 2 * DN = 3 * 2 = 6 см NR = MK = 6cм по свойству противолежащих сторон параллелограмма, MN = KR = 5см по свойству противолежащих сторон параллелограмма. P = 2 * MN +..

Угол АВС = углу BDE = 127° уголBEA = углуBDC = 90° четырехугольник MEBD(Сумма углов в четырехугольнике равна 360° угол EMB = 360° — 90° — 90° — 127° = 53° Ответ : 53°.

∠ABC = ∠EBD = 127° — как вертикальные. ∠DME = 360° — ∠MEC — ∠MDA — ∠EBD = 360° — 90° — 90° — 127° = 53°. Ответ : 53°.

Вариант решения. Ответ : 20°Объяснение : Диагонали прямоугольника равны и точкой пересечения делятся пополам. Пусть диагонали пересекаются в точке О. OB = OA, ∆ ВОА — равнобедренный. Из суммы углов треугольника ∠ОВА = ∠ОАВ = (180° — 40°) : 2 = 70..

Дано : ABCD — прямоугольник ; AC∩BD = O ; F∈AO ; BF⊥AO ; ∠AOB = 40°. Найти : ∠ABF. Решение : ∠FOB = ∠AOB = 40° — как углы с одинаковыми сторонами. ΔBFO — прямоугольный т. К. BF ⊥ AO. Значит ∠FBO = 90° — ∠FOB (т. К. сумма острых углов в прямоуго..

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Если дуга окружности составляет 80 то центральный угол 40

Найдите значение выражения

Решение . Вынесем общий множитель за скобки:

Одна из точек, отмеченных на координатной прямой, соответствует числу Какая это точка?

Решение . Возведём в квадрат числа 6, 7, 8:

Число 39 лежит между числами 36 и 49 и находится ближе к числу 36, поэтому соответствует точке M.

Правильный ответ указан под номером 1.

Площадь территории Испании составляет 506 тыс. км 2 . Как эта величина записывается в стандартном виде?

В ответе укажите номер правильного варианта.

Решение . Преобразуем число к стандартному виду:

Правильный ответ указан под номером: 4.

Решите уравнение

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение . Последовательно получаем:

На одном из рисунков изображен график функции Укажите номер этого рисунка.

Решение . График функции проходит через точку (−1; 2). Этому условию удовлетворяет только график, изображённый на рисунке 4.

Правильный ответ указан под номером 4.

Геометрическая прогрессия задана условием Найдите сумму первых её 4 членов.

Решение . Найдём знаменатель геометрической прогрессии:

Первый член данной прогрессии равен Сумма первых k членов геометрической прогрессии может быть найдена по формуле:

Необходимо найти имеем:

Упростите выражение , найдите его значение при . В ответ запишите полученное число.

Решение . Упростим выражение:

Найдём значение выражения при :

Решите неравенство

В ответе укажите номер правильного варианта.

Решение . Последовательно получаем:

Правильный ответ указан под номером: 2.

В трапеции ABCD AB = CD, ∠BDA = 49° и ∠BDC = 13°. Найдите угол ABD. Ответ дайте в градусах.

Решение . Угол ADC равен ∠ADC = ∠BDA + ∠BDC = 49° + 13° = 62°. Трапеция ABCD — равнобедренная, следовательно, углы при основаниях равны, то есть ∠BAD = ∠ADC = 62°. Сумма углов треугольника равна 180°, откуда из треугольника ABD получаем, что ∠ABD = 180° − (∠BAD + ∠ADB) = 180° − (62° + 49°) = 69°.

Центральный угол AOB, равный 60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.

Решение . Рассмотрим треугольник AOB: он равнобедренный, т. к. его боковые стороны равны радиусу. Углы при основании равнобедренного треугольника равны. Пусть BAO равен x, тогда x + x + 60° = 180°, где x = 60°. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, AO = 3.

Сторона квадрата равна 10. Найдите его площадь.

Решение . Площадь квадрата равна квадрату его стороны, поэтому она равна 100.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.

Решение . Заметим, что высота, опущенная из точки B на сторону AC равна 4.

Какие из следующих утверждений верны?

1) Через любые три точки проходит не более одной окружности.

2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение . Проверим каждое из утверждений.

1) «Через любые три точки проходит не более одной окружности.» — верно, Через любые три точки, не лежащие на одной прямой, проходит единственная окружность. Если точки лежат на одной прямой, то окружность провести невозможно. Тем самым, через любые три точки можно провести не более одной окружности.

2) «Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.» — верно, если расстояние от центра до прямой меньше радиуса, то окружности имеют две общие точки, если окружности касаются то окружности имеют одну общую точку, если расстояние больше радиуса, то окружности не имеют общих точек.

3) «Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются» — неверно, окружность, радиус которой равен 3, лежит внутри окружности с радиусом 5.

4) «Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.» — верно, вписанный угол измеряется половиной дуги,на которую он опирается.

Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Если дуга окружности составляет 80 то центральный угол 40

Вопрос по геометрии:

Если дуга окружности Составляет 80°, то центральный угол, опирающийся на эту же дугу, равен 40°

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 2

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

🌟 Видео

Окружнось, дуга, длина дуги, центральный угол.Скачать

Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать

Как найти длину дуги окружности центрального угла. Геометрия 8-9 классСкачать

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

❓ Угол между секущими (вне окружности)Скачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ|Найдите вписанный угол, опирающийся на дугу, которая составляет 1/5 окружностСкачать

11 класс, 40 урок, Угол между касательной и хордойСкачать

Центральный уголСкачать

Угол между хордой и касательнойСкачать

Окружность и углы. 8-9 класс, геометрия. Хорда, касательная, вписанный и центральный углы. Дуга.Скачать

Центральный угол на 48° больше острого вписанного углаСкачать

ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Угол между хордой и касательнойСкачать

8 класс, 34 урок, Теорема о вписанном углеСкачать

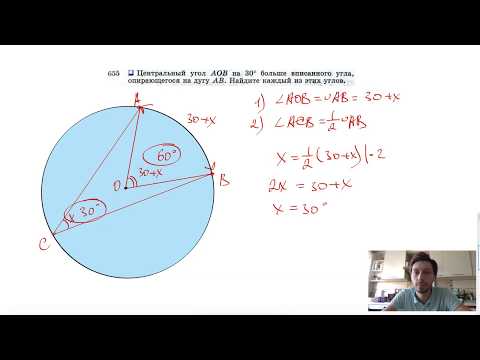
№655. Центральный угол АОВ на 30° больше вписанного угла, опирающегося на дугу АВ. НайдитеСкачать

Как понять центральные и вписанные углыСкачать

Промоурок по математике на тему: "Углы в окружности! Бывает и такое!"Скачать