Видео:Физика Электрон, разогнанный разностью потенциалов U = 2 кВ, влетает в однородное магнитное полеСкачать
Ваш ответ
Видео:Физика Электрон влетает в однородное магнитное поле под прямым углом к линиям магнитной индукцииСкачать

решение вопроса
Видео:Физика Электрон влетает в однородное магнитное поле со скоростью 10000 км/с и движется по окружностиСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,989
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:МАГНИТНОЕ ПОЛЕ за 24 минуты. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать

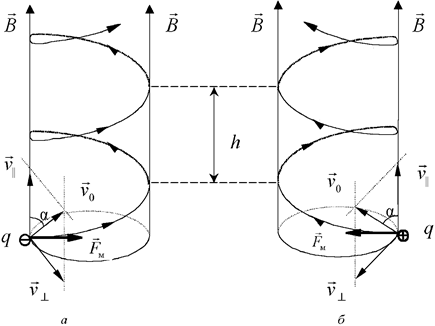
Электрон влетает в однородное магнитное поле под углом к вектору
Электрон, ускоренный разностью потенциалов U = 6 кВ, влетает в однородное магнитное поле под углом α = 30° к направлению поля и движется по винтовой траектории. Индукция магнитного поля B = 13 мТл. Найти радиус R и шаг h винтовой траектории.
Дано:
U = 6 кВ = 6·10 3 В
В = 13 мТл = 13 ·10 -3 Тл
Решение:
Разложим вектор скорости ν частицы на две составляющие (рис.): v 1 , направленную вдоль линий магнитной индукции, и v2, перпендикулярную этим линиям. Модули этих составляющих — соответственно υ 1 = ν cos α и v 2 = υ sin α
На частицу действует сила Лоренца, обусловленная со ставляющей v 2 . Вследствие этого частица движется по окружности со скоростью v 2 в плос кости, перпендикулярной магнитному полю. Радиус этой окружности определим, составив уравнение на основании второго закона Ньютона.
По второму закону Ньютона F Л = m е a, где a = υ 2 / R — центростремительное ускорение.
Скорость найдем из закона сохранения энергии
Одновременно частица будет двигаться и вдоль поля. Это равномерное движение со скоростью v 1 , так как состав ляющая v 1 не вызывает появления силы Лоренца. В ре зультате одновременного движения по окружности и по прямой частица будет двигаться по винтовой линии, «навиваясь» на линии магнитной индукции. Шаг винтовой линии
где Т — период обращения частицы по окружности:
получаем шаг винтовой линии
Ответ: 
Видео:Физика Заряженная частица, разогнанная разностью потенциалов U влетает в однородное магнитное полеСкачать
Шаг винтовой линии электрона
Электрон, ускоренный разностью потенциалов U = 6 кВ, влетает в однородное магнитное поле под углом α = 30° к направлению поля и движется по винтовой траектории. Индукция магнитного поля B = 13 мТл. Найти радиус R и шаг h винтовой траектории.
Дано:
U = 6 кВ = 6·10 3 В
В = 13 мТл = 13 ·10 -3 Тл
Решение:
Разложим вектор скорости ν частицы на две составляющие (рис.): v 1 , направленную вдоль линий магнитной индукции, и v2, перпендикулярную этим линиям. Модули этих составляющих – соответственно υ 1 = ν cos α и v 2 = υ sin α
На частицу действует сила Лоренца, обусловленная со ставляющей v 2 . Вследствие этого частица движется по окружности со скоростью v 2 в плос кости, перпендикулярной магнитному полю. Радиус этой окружности определим, составив уравнение на основании второго закона Ньютона.
По второму закону Ньютона F Л = m е a, где a = υ 2 / R – центростремительное ускорение.
Скорость найдем из закона сохранения энергии
Одновременно частица будет двигаться и вдоль поля. Это равномерное движение со скоростью v 1 , так как состав ляющая v 1 не вызывает появления силы Лоренца. В ре зультате одновременного движения по окружности и по прямой частица будет двигаться по винтовой линии, «навиваясь» на линии магнитной индукции. Шаг винтовой линии
где Т — период обращения частицы по окружности:
получаем шаг винтовой линии
Ответ:
Заряд q влетает со скоростью 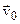
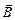
Рис. 12.7. Траектория движения заряда в магнитном поле:
а – отрицательный заряд; б – положительный заряд
Уравнение движения электрона определяется II законом Ньютона (12.1) с учетом магнитной силы (11.9)
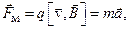
где q – заряд электрона.
Разложим скорость на составляющие, направленные параллельно и перпендикулярно вектору 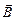
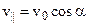
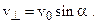
При движении электрона со скоростью 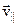
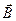
При движении электрона со скоростью 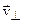
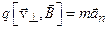
или, в скалярном виде,
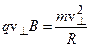
электрон будет двигаться по окружности радиусом
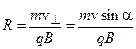
В результате сложения этих двух движений электрон будет двигаться по винтовой линии радиусом R и шагом винта h:
где T – период движения по окружности:
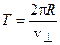
Таким образом получаем, что шаг винта будет равен:
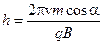
1. Как будет двигаться заряженная частица, влетевшая в однородное магнитное поле под углом в вектору 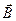
2. Если заряженная частица, пролетая некоторую область про-
странства, не отклоняется от первоначального направления движения, можно ли утверждать, что магнитное поле в этой области пространства отсутствует?
3. Протон и электрон, имеющие одинаковую скорость, попадают в однородное магнитное поле, индукция которого В перпендикулярна скорости зарядов. Как будут отличаться траектории заряженных частиц?
4. Чему равна работа силы, действующей на электрон, движущийся в однородном магнитном поле с индукцией В?
5. Покажите, что какой бы скоростью ни обладал электрон, влетающий в однородное магнитное поле с индукцией В, и каков бы ни был угол α между векторами 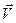
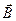
6. Какова форма траектории электрона, движущегося в совпадающих по направлению электрическом и магнитном полях, в случаях, когда: 1) начальная скорость электрона направлена вдоль полей, 2) скорость электрона перпендикулярна к Е и В?
7. Можно ли определить, каким полем вызвано отклонение пучка протонов, попавшего в некоторую область пространства, – электрическим или магнитным?
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: «Что-то тут концом пахнет». 8526 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

§14. Движение заряженных частиц в электрическом и магнитном полях
14.3 Движение по винтовой линии в однородном магнитном поле.
Рассмотрим теперь произвольный случай движения заряженной частицы в однородном магнитном поле.
Введем систему декартовых координат, так, чтобы вектор индукции однородного магнитного поля (
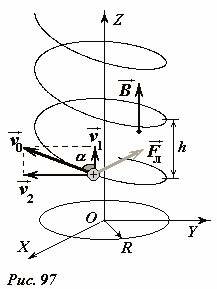
vec B) был направлен вдоль оси Oz (рис. 97). Пусть вектор скорости (
vec upsilon_0) частицы массы m, имеющей электрический заряд q, направлен под произвольным углом α к вектору индукции поля. Разложим этот вектор на две составляющих[
vec upsilon_1] – параллельную вектору индукции и (
vec upsilon_2) – перпендикулярную ему. Действующая на частицу сила Лоренца (
vec F_L) перпендикулярна векторам скорости и индукции, то есть лежит в плоскости xOy. Модуль этой силы равен
F_L = q upsilon_0 B sin alpha = q upsilon_2 B) . (1)
Если спроецировать уравнение второго закона Ньютона для частицы
m vec a = q vec upsilon imes vec B) , (2)
на плоскость xOy, то получим уравнение, в которое только компонента скорости, перпендикулярная полю. Это уравнение описывает движение частицы, движущейся перпендикулярно вектору индукции, которое было подробно рассмотрено ранее. Оно представляет собой равномерное движение по окружности радиуса
и угловой скоростью
не зависящими, ни от модуля скорости частицы, ни от ее направления.
Проекция магнитной силы на ось Oz равна нулю, поэтому проекция скорости на эту остается постоянной. Следовательно, эта координата изменяется по линейному закону
z = z_0 + upsilon_1 t = z_0 + upsilon_0 t cos alpha) . (6)
Таким образом, движение частицы можно представить в виде суперпозиции равномерного движения вдоль оси Oz и равномерного движения по окружности в перпендикулярной плоскости. Траекторией этого движения является винтовая линия, радиус которой определяется формулой (3), а шаг рассчитывается по формуле
h = upsilon_1 t = 2 pi frac cos alpha) . (7)
Таким образом, заряженные частицы движутся по спиралям (точнее винтовым линиям), навивающимся на силовые линии магнитного поля. Такой же характер движения сохраняется и в неоднородном магнитном поле – частицы движутся по спиралям, навивающимся на силовые линии поля, при этом радиус и шаг спирали плавно изменяются с изменением индукции поля. Направление смещения (дрейфа) частиц в магнитном поле определяется направлением начальной скорости частиц и не зависит ни от знака заряда частицы, ни от направления вектора индукции поля, последние определяют только направление вращения вокруг силовой линии. Такое движение заряженных частиц позволяет конструировать различные «магнитные ловушки» для накопления заряженных частиц, управлять движением сильно ионизованного газа (плазмы). Аналогичный характер имеет движение заряженных частиц и в магнитном поле Земли.
🎦 Видео
Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Физика - Магнитное полеСкачать

Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать

Электронный штангенциркуль 0.01 мм. Точный металлический штангенциркуль с Алиэкспресс.Скачать

Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Устройство необходимое всем мастерам бытовых электроприборов. Индикатор межвиткового замыкания.Скачать

Магнитное поле. Магнитная индукция | Физика 11 класс #1 | ИнфоурокСкачать

Сила ЭЛЕКТРОНА - в его отсутствии. ЭЛЕКТРОНА НЕ СУЩЕСТВУЕТ! // Часть 1Скачать

Электромагнитная индукция. ЕГЭ Физика. Николай НьютонСкачать

МАГНИТНАЯ ИНДУКЦИЯ 11 класс физика сила Ампера сила ЛоренцаСкачать

Урок 278. Задачи на силу Лоренца - 1Скачать

Урок 270. Магнитное поле и его характеристикиСкачать

Ион в однородном магнитном полеСкачать