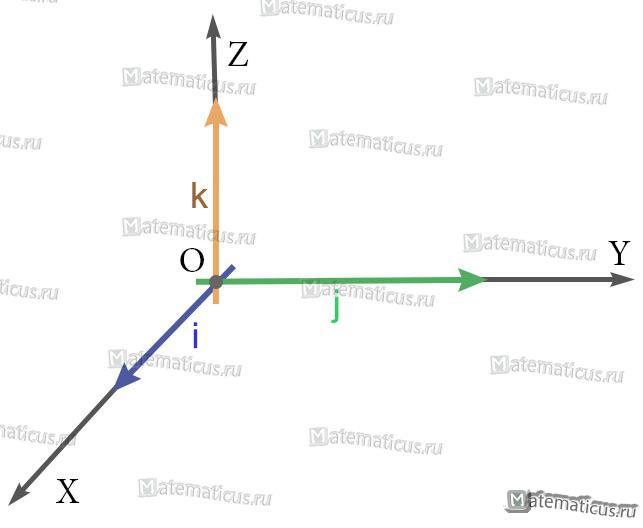
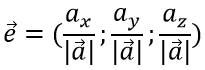Единичный вектор оси ox

Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.

i — единичный вектор оси абсцисс;

j — единичный вектор оси ординат;

k — единичный вектор оси аппликат.

i⊥j⊥k, i=j=k=1

В прямоугольной системе координат в пространстве координаты векторов равны:

i(1;0;0), j(0;1;0), k(0;0;1)

Единичные векторы являются некомпланарными.

Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.

a=xi+уj+zk

где x, y, z — координаты вектора проекции на соответствующие координатные оси.

Эта формула называется разложением вектора по ортам координатных осей.

Единичный вектор определяется по формуле:

Дан вектор а = (1; 2; -2)

Требуется найти длину (модуль) и единичный вектор e направления вектора а

Находим длину вектора a

затем вычисляем единичный вектор e

Видео:Единичный векторСкачать

Векторное произведения единичных векторов

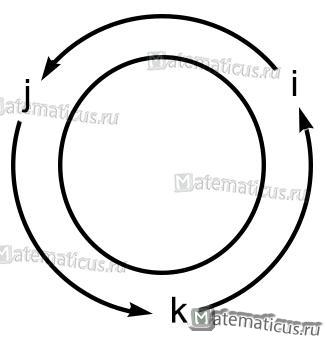
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.

На основании схемы получаем таблицу векторного произведения единичных векторов

Пример 1
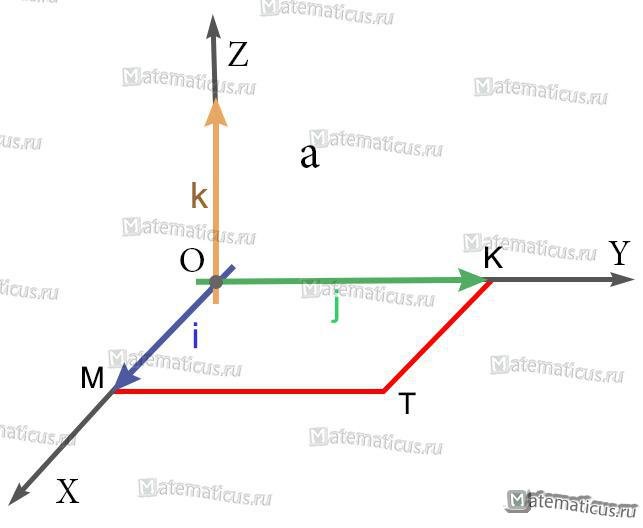
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.

Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).

iхj=k

Пример 2
Найти векторное произведение jхi.

Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.5 / 5. Количество оценок: 4

Видео:Единичные векторы Декартовой системы координатСкачать

Единичный вектор оси ox

Получите бесплатный курс по основам математики. Эти знания необходимы для решения задач по физике.

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Векторная алгебра с нуля!

Получите бесплатный курс по Векторной алгебре. Он необходим для решения задач по физике.

Видео:Построение проекции вектора на осьСкачать

Книги по изучению физики и для подготовки к ЕГЭ

Видео:Разложение вектора по базису. 9 класс.Скачать

Единичные векторы. Орты. Декартова система координат

Единичный вектор — это вектор, абсолютная величина (модуль) которого равен единице. Для обозначения единичного вектора мы будем использовать нижний индекс е. Так, если задан вектор а, то его единичным вектором будет вектор а_е. Этот единичный вектор направлен туда же, куда направлен и сам вектор а, и его модуль равен единице, то есть а_е = 1.

Очевидно, а = а·а_е (а — модуль вектора а). Это следует из правила, по которому выполняется операция умножения скаляра на вектор.

Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат.

Напомню, что декартовой системой координат в пространстве традиционно называется тройка взаимно перпендикулярных осей, пересекающихся в точке, которая называется началом координат. Координатные оси обычно обозначают буквами X , Y , Z и называют соответственно осью абсцисс, осью ординат и осью аппликат. Сам Декарт пользовался только одной осью, на которой откладывались абсциссы. Заслуга использования системы осей принадлежит его ученикам. Поэтому фраза декартова система координат исторически ошибочна. Лучше говорить прямоугольная система координат или ортогональная система координат. Тем не менее, изменять традиции мы не станем и в дальнейшем будем считать, что декартова и прямоугольная (ортогональная) системы координат — это одно и то же.

Единичный вектор, направленный вдоль оси Х, обозначается i, единичный вектор, направленный вдоль оси Y , обозначается j, а единичный вектор, направленный вдоль оси Z, обозначается k. Векторы i, j, k называются ортами (рис. 12, слева), они имеют единичные модули, то есть
i = 1, j = 1, k = 1.

Оси и орты прямоугольной системы координат в некоторых случаях имеют другие названия и обозначения. Так, ось абсцисс X может называться касательной осью, а ее орт обозначается τ (греческая строчная буква тау), ось ординат – осью нормали, ее орт обозначается n , ось аппликат – осью бинормали, ее орт обозначается b. Зачем менять названия, если суть остается той же?

Дело в том, что, например, в механике при изучении движения тел прямоугольная система координат используется очень часто. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i, j, k.

Но нередко, когда объект движется по какой-то криволинейной траектории (например, по окружности) бывает удобнее рассматривать механические процессы в системе координат, движущейся с этим объектом. Именно для такой движущейся системы координат и используются другие названия осей и их ортов. Просто так принято. В этом случае ось X направляют по касательной к траектории в той ее точке, в которой в данный момент этот объект находится. И тогда эту ось называют уже не осью X, а касательной осью, а ее орт обозначают уже не i, а τ. Ось Y направляют по радиусу кривизны траектории (в случае движения по окружности – к центру окружности). А поскольку радиус перпендикулярен касательной, то ось называют осью нормали (перпендикуляр и нормаль – это одно и то же). Орт этой оси обозначают уже не j, а n. Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это – бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.

Книги по изучению физики и для подготовки к ЕГЭ
Эти книги должен иметь каждый старшеклассник, абитуриент и студент!

Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Координаты вектора в математике

Координаты вектора ― это коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

Содержание:

Видео:Урок 9. Проекции вектора на координатные осиСкачать

Координаты вектора

Для введения понятия координат вектора следует рассмотреть возможность разложения вектора по осям координат. Мы хотим каждый вектор задать парой чисел — проекциями этого вектора на оси координат. При таком подходе действия над векторами можно свести к действиям с парами чисел.

Определим проекции вектора на координатную ось. Пусть задана координатная ось Ох. Единичный отрезок ОЕ теперь будем считать единичным вектором , т. е. вектором, длина которого равна 1 (рис. 2.506).

Возьмем любой вектор и отложим его от некоторой точки А:

Спроектируем точки А и В на ось Ох. Получим точки и составляющую вектора по оси Ох (рис. 2.507). Ее длина со знаком «плюс» или «минус» и называют проекцией вектора на ось Ох.

Определение. Проекцией вектора на ось Ох называют длину его составляющей по этой оси, взятую со знаком «плюс» или «минус». При этом берется знак «плюс», если направление вектора совпадает с направлением оси Ох, и знак «минус», если эти направления противоположны. Если = 0, т. е.

Проекция точки — точка, проекция отрезка — отрезок (или точка), а проекция вектора — число.

Вектор получается из коллинеарного ему единичного вектора умножением на . При этом если сонаправлен с , то Если же противоположно направлен , то

Следовательно, имеет место равенство

Можно доказать следующие свойства проекций векторов на ось.

1. Равные векторы имеют равные проекции на заданную ось.

2. При сложении векторов их проекции на ось складываются.

3. При умножении вектора на число его проекция умножается на это число.

Прежде чем ввести понятие координат вектора, докажем теорему.

Теорема 6. Пусть на плоскости введена прямоугольная система координат с единичными векторами координатных осей Ох и Оу. Пусть — некоторый вектор, а — его проекции на оси координат. Тогда вектор единственным образом представляется в виде (рис. 2.508).

Выше получена формула для разложения вектора а по векторам (с учетом обозначения): .

Пару чисел называют координатами вектора в данной системе координат.

Координаты вектора в пространстве определяются так же, как на плоскости. Справедлива следующая теорема.

Теорема 7. Пусть в пространстве введена прямоугольная система координат с единичными векторами координатных осей Ох, Оу, Oz. Тогда вектор единственным образом представляется в виде (рис. 2.509).

Числа называются координатами вектора относительно векторов, которые называются базисными векторами или, короче, базисом.

Введенные координаты вектора позволяют получить формулу длины вектора.

Рассмотрим рисунок 2.508.

1. Если точка А не лежит на координатных осях, то треугольник прямоугольный.

2. (1, теорема Пифагора).

3. Так как то получаем, что (2).

4. Но поэтому

(3, 4).

Формула справедлива и в тех случаях, когда точка А лежит на какой-то оси координат.

Свойства координат вектора

В курсе геометрии нам практически не приходится работать с векторами в координатах (это приходится делать в курсе физики). Можно доказать различные свойства координат вектора:

1. Координаты равных векторов соответственно равны. Обратно: векторы, имеющие соответственно равные координаты, равны.

2. При сложении векторов их соответствующие координаты складываются. А именно, если

3. При умножении вектора на число его координаты умножаются на это число. А именно, если

Координаты вектора связаны с координатами точки по следующему правилу: чтобы найти координаты вектора, нужно от координат конца вектора отнять координаты начала вектора.

В частности, если вектор отложен от начала координат, то координаты вектора равны координатам его конца.

Возьмем в пространстве некую прямоугольную систему координат с началом в точке О и координатными осями х, у, z (рис. 2.510). Пусть А, В, С — точки с единичными координатами на этих осях, т. е. А(1, 0, 0), В(0, 1, 0), С(0, 0, 1).

Тогда векторы — это направляющие единичные векторы координатных осей х, у, z.

Возьмем любую точку М(х, у, г), и пусть — ее радиус-вектор.

Теорема 8. Координаты точки М соответственно равны координатам ее радиус-вектора относительно базиса .

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

🌟 Видео

Единичные векторы и инженерная запись (видео 34) | Криволинейное движение | ФизикаСкачать

Векторные величины Проекция вектора на осьСкачать

#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Координаты вектора. 9 класс.Скачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Основы кинематики. Тема 3. Проекция вектора на осьСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Единичные базисные векторы.Часть 2 (видео 36) | Криволинейное движение | ФизикаСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Векторы #3: многомерные системы координат, базисные векторыСкачать

§1 ВекторыСкачать

Математика. Разложение вектора по ортам координатных осейСкачать