Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 3 и 2.
а) Пусть АВ — диаметр большей из трёх окружностей, О — её центр, O1 — центр окружности радиуса r у касающейся окружности с диаметром АВ в точке А, O2 — центр окружности радиуса R, касающейся окружности с диаметром АВ в точке С, окружности с центром O1 — в точке D, отрезка АВ — в точке Е. Точки О, O2 и С лежат на одной прямой, поэтому OO2 = ОС − O2С = ОС − R. Аналогично ОО1 = OA − О1А = ОА − r и O1O2 = O1D + O2D = r + R. Следовательно, периметр треугольника OO1O2 равен
а так как О1E = OO1 + ОЕ, то Из этого уравнения находим, что R = 0,96 .
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 507237: 507211 515670 Все
- Технологическая карта урока геометрии в 8 классе «Касающиеся окружности»
- Задача №1 Решение:
- Ответ: 9
- Задача №3 Решение:
- Краткое описание документа:
- Две касающиеся окружности одинакового радиуса 0, 75 находятся внутри третьей окружности и касаются ее так, что диаметры всех этих трех окружностей лежат на одной прямой?
- В окружности радиуса К проведён диаметр и на нём взята точка А на расстоянии а от центра?
- РЕБЯТА, ОЧЕЕНЬ СРОЧНО?
- Две окружности касаются внешним образом?
- Докажите, что если две окружности касаются, то точка касания и центры этих окружностей лежат на одной прямой?
- Две окружности касаются внешним образом?
- Две окружности касаются внутренним образом?
- Каждая из трех окружностей касается двух других?
- В окружность радиуса 16 см на расстоянии 2 см от центра проведена хорда?
- Две окружности касаются внешним образом?
- Найдите геометрическое место центров окружностей одного радиуса, касающихся данной окружности внешним образом?
- 💥 Видео
Видео:Олимпиадная задача за 8 класс/Подготовительную Группу Яслей СССРСкачать

Технологическая карта урока геометрии в 8 классе «Касающиеся окружности»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Технологическая карта урока геометрии в 8 классе по теме
Ценова Елена Николаевна , учитель математики
Тип урока : урок обобщения, повторения и формирования новых знаний.
Вид урока : комбинированный.
Цель: Создать условия для систематизации знаний о случаях внешнего и внутреннего касания окружностей и формирование умения решать задачи с опорой на эти знания.
Повторить ранее изученный материал.
Обобщить и систематизировать знания учащихся о возможных случаях касания окружностей.
Применить полученные знания при решении задач разного уровня сложности, в том числе задач ОГЭ и и ЕГЭ.
Формировать познавательную мотивацию.
Развивать пространственное представление, геометрическое мышление.
Личностные: у меть проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные: работа над понятием информация-знание; развивать познавательную деятельность учащихся.
Предметные: иметь представление о возможных случаях касания окружностей; применять знания при решении задач .
Познавательные УУД: умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение.
Коммуникативные УУД: умение находить общее решение и решать конфликты на основе согласования позиций и учета интересов.
Регулятивные УУД: умение адекватно оценивать правильность или ошибочность выполнения учебной задачи.
Личностные УУД: способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Формы урока: индивидуальная; фронтальная; групповая.
Оборудование: ПК, проектор и экран.
Преподавание ведется по учебнику Геометрия 7-9 классов общеобразовательных учреждений / под редакцией Л.С. Атанасяна и др. М.: Просвещение, 2013 год.
Цель этапа : создать
настрой на работу
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
Включаются в деловой ритм урока.
Умение совместно договариваться о правилах поведения и общения.
2. Актуализация знаний и умений
Цель этапа: напомнить предыдущий изученный материал, на базе какого будут усваиваться новые знания.
Ребята, в качестве повторения теоретического материала, я предлагаю Вам разгадать кроссворд.
— Один мудрец сказал: « Окружность – душа геометрии. Познайте окружность и вы не только познаете душу геометрии, но и возвысите душу свою». Как вы понимаете его слова?
— Попробуйте решить софизм.
Вспоминают пройденный материал, дают объяснения на поставленные вопросы самостоятельно, сравнивают свои ответы с изображением на экране.
Осмысливают слова мудреца, высказывают свои мнения.
Вспоминают, что такое софизм (Софизмом называют умышленно-ложное умозаключение, которое имеет видимость правильного.
Приходят к выводу, что нарушено применение признака равенства треугольников.
Умение ориентироваться в своей системе знаний.
Умение слушать и слышать; формулировать устные высказывания.
Умение соотнесения того, что уже известно и усвоено, и того, что ещё неизвестно; умение определения последовательности промежуточных целей с учётом конечного результата; составление плана и последовательности
Умение устанавливать причинно-следственные связи, мыслить аналитически.
Умение выражать свои мысли, аргументировать свое решение.
Умение адекватно реагировать на трудности и не боятся сделать ошибку.
3. Целеполагание и мотивация
Цель этапа: обеспечить у учащихся ощущение продвижения вперед, переживания успеха в учебной деятельности.
— Определиться с темой сегодняшнего урока нам поможет кроссенс. Что можно расположить в центре таблицы? Ваша задача – объяснить кроссенс, составить рассказ — ассоциативную цепочку, посредством взаимосвязи изображений; вывести тему урока.
Учащиеся дают определение кроссенса. Кроссенс — это головоломка, которая состоит из 9 квадратиков, в которых помещены изображения. Девять изображений расставлены таким образом, что каждая картинка имеет связь с предыдущей и
центральная объединяет по смыслу сразу несколько. Объясняют кроссенс и самостоятельно выводят тему урока «Касающиеся окружности».
Предполагаемые ответы учеников:
1. Окружность. Касание окружностей бывает
внешним и внутренним.
касаются внешним образом (касаются извне), если их центры лежат по разные стороны от их общей касательной. Если две окружности касаются, то точка касания лежит на прямой, соединяющей центры. Кроме того, эта прямая перпендикулярна касательной, проведённой в точку касания окружностей.
касаются внутренним образом (касаются изнутри), если их центры лежат по одну сторону от их общей касательной. Линия
центров двух касающихся окружностей проходит через точку касания.
4. Можно рассмотреть касание не только 2-х окружностей, но и 3-х, 4-х. Здесь три окружности разных радиусов попарно касаются друг друга внешним образом. К ним проведена общая касательная.
касание 3-х окружностей. Две окружности касаются третьей – одна изнутри другая извне.
6. Две окружности
касаются друг друга внешним образом, причём, каждая из них изнутри касается третьей окружности.
7. В угол вписаны две окружности, касающиеся друг друга внешним образом.
8. Три окружности
касаются друг друга внешним образом, причём, каждая из них изнутри касается четвёртой окружности.
Умение структурировать информацию в нужной форме.
Умение ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что ещё неизвестно.
Организация совместного обсуждения, установления сотрудничества с учителем, речевая коммуникация. Проявление интереса к новому содержанию.
4. Первичное усвоение новых знаний.
Цель этапа: помочь усвоить учащимися новый материал с помощью активной деятельности на уроке, осмыслить определенные понятия , организовать решение и объяснение задания.
Организует в группах самостоятельную работу. Решение задач полуустно.
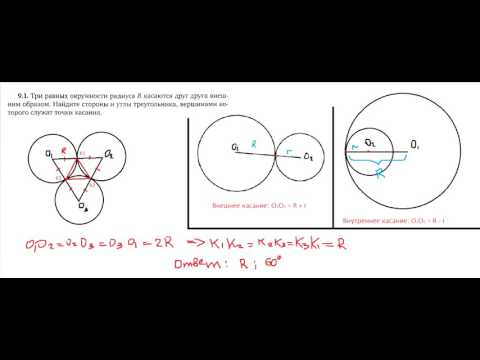
Задача №1 Три равных окружности радиуса R касаются друг друга внешним образом. Найдите углы треугольника, вершинами которого служат точки касания.
Задача №2 Две равных окружности касаются изнутри третьей и касаются между собой. Соединив три центра, получим треугольник с периметром, равным 18. Найдите радиус большей окружности.
Задача №3 Три окружности радиусов 6, 7 и 8 попарно касаются друг друга внешним образом. Найдите площадь треугольника с вершинами в центрах этих окружностей.
Задача №4 Три окружности разных радиусов попарно касаются друг друга внешним образом. Отрезки, соединяющие их центры, образуют прямоугольный треугольник. Найдите радиус меньшей окружности, если радиусы большей и средней равны 6 и 4.
Учитель осуществляет взаимооценивание интересным приёмом «Кулак-ладонь».
Сущность метода направлена на формирование навыков самооценивания и самоуправления:
раскрытая ладонь, если они ученики уверены, что достигли целей и ожидаемых результатов;
три пальца вверх, если они считают, что частично преуспели в достижении целей, но следует еще поработать;
кулак, если они считают, что сделали незначительные успехи или совсем ничего для достижения цели.
Решают задачи по карточкам в группах самостоятельно.
Задача №1 Решение:
Рассмотрим равносторонний треугольник с вершинами в центрах окружностей. Его стороны равны 2R. Стороны искомого треугольника являются его средними линиями, поэтому равны R.
Ответ: 60 0 ; 60 0 ; 60 0 .
Пусть радиусы данных окружностей равны r , r и R ( r R ). Тогда стороны указанного треугольника равны R — r , R — r и 2 r . Поэтому
Следовательно, R = 9.
Ответ: 9
Задача №3 Решение:
Линия центров двух касающихся окружностей проходит через их точку касания, поэтому стороны треугольника с вершинами в центрах окружностей равны 13, 14 и 15. Пусть S — площадь треугольника, p-п олупериметр. Тогда p=
S=


Задача №4 Решение:
Пусть x – радиус меньшей окружности. Стороны получившегося треугольника равны 10, 6 + x и 4 + x.
Поскольку 10 – наибольшая сторона, это гипотенуза. Значит, (x + 6)² + (x + 4)² = 100, откуда x = 2.
Умение строить рассуждения в форме связи простых суждений об объекте, ориентироваться в своей системе знаний, умение производить выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
Умение контролировать и оценивать свои действия, саморегуляция как способность к мобилизации сил и энергии, к волевому усилию (к выбору в ситуации мотивационного конфликта) и преодолению препятствий.
Умение осуществлять инициативное сотрудничество в поиске, сборе и структурировании информации. Формирование внутренней позиции, адекватной мотивации учебной деятельности, умение замечать и признавать расхождение своих поступков со своими заявленными позициями.
5. Контроль усвоения, обсуждение ошибок и их коррекция
Цель этапа : закрепление знаний и способов действий.
Решение задачи с полным оформлением.
Задача №5 Две окружности радиуса r касаются друг друга. Кроме того, каждая из них касается извне третьей окружности радиуса R в точках A и B
соответственно. Найдите радиус r, если AB = 12, R = 8.
Умение преобразовывать информацию из одной формы в другую, самостоятельно создавать алгоритмы деятельности при решении проблем творческого и поискового характера.
Выделения и осознания обучающимися того, что уже усвоено и что ещѐ нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы; умение вносить необходимые коррективы в действие.
Умение оформлять свои мысли в устной и письменной форме, умение осуществлять самооценку на основе критерия успешности учебной деятельности.
6. Домашнее задание.
Цель этапа: выделить основные моменты по выполнению домашнего задания .
Даёт пояснения к выполнению домашнего задания. Обеспечивает понимание детьми цели, содержания и способов выполнения домашнего задания.
1) Дана окружность радиуса R . Четыре окружности равных радиусов касаются данной внешним образом, и каждая из этих четырёх окружностей касается двух других. Найдите радиусы этих четырёх окружностей.
2) В угол, равный 60 о , вписаны две окружности, касающиеся друг друга внешним образом. Радиус меньшей окружности равен r . Найдите радиус большей окружности.
Слушают речь учителя, читают текст задач домашнего задания.
Способность использовать полученные знания при выполнении домашнего задания.
Умение работать по плану.
7. Рефлексия учебной деятельности на уроке
Подведение итогов урока.
Организует рефлексию, соотносит цель и результаты учебной деятельности, намечает дальнейшие цели деятельности
— Давайте подведём итоги. Представьте, что сегодняшний урок вы провели в ресторане. Ответьте на вопросы:
С оотносят цели урока и результаты собственной деятельности.
Анализируют свою деятельность на уроке, отвечая на вопросы учителя.
Умение выражать свои мысли, строить высказывание в соответствие с задачами коммуникации. Умение размышлять, заниматься самонаблюдением; самоанализ, осмысление, условий и результатов собственной деятельности.
Умение проговаривать последовательность действий на уроке, оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки.
Умение осуществлять самооценку на основе критерия успешности учебной деятельности, формирование внутренней позиции, ориентируемой на моральные нормы
Краткое описание документа:
Технологическая карта разработана с учётом требований ФГОС. Данный урок позволяет обобщить и систематизировать знания учащихся о случаях внешнего и внутреннего касания окружностей и применить полученные знания при решении задач разного уровня сложности, в том числе задач ОГЭ и и ЕГЭ.
Видео:Занятие 1 к главе 9Скачать
Две касающиеся окружности одинакового радиуса 0, 75 находятся внутри третьей окружности и касаются ее так, что диаметры всех этих трех окружностей лежат на одной прямой?
Геометрия | 5 — 9 классы
Две касающиеся окружности одинакового радиуса 0, 75 находятся внутри третьей окружности и касаются ее так, что диаметры всех этих трех окружностей лежат на одной прямой.
Найтиде радиус окружности, касающейся всех трех данных окружностей.
Странно что так долго никто не решил .
Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

В окружности радиуса К проведён диаметр и на нём взята точка А на расстоянии а от центра?
В окружности радиуса К проведён диаметр и на нём взята точка А на расстоянии а от центра.
Найти радиус второй окружности, которая касается диаметра в точке А и изнутри касается данной окружности.
Видео:Геометрия Две окружности радиуса R с центрами O1 и O2 касаются друг друга. Их пересекает прямаяСкачать

РЕБЯТА, ОЧЕЕНЬ СРОЧНО?
РЕБЯТА, ОЧЕЕНЬ СРОЧНО.
Касающиеся друг друга внешним образом две окружности радиусов 3 и 12 касаются прямой, по одну сторону от ко¬торой они располагаются.
Найдите радиусы каждой из окружностей, касающихся данных двух окружностей и прямой.
Видео:Касание окружностей | Задачи 16-21 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Две окружности касаются внешним образом?
Две окружности касаются внешним образом.
Радиус одной окружности на 3 см меньше радиуса другой окружности.
Найдите диаметры окружностей, если расстояние между их центрами равно 11 см.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Докажите, что если две окружности касаются, то точка касания и центры этих окружностей лежат на одной прямой?
Докажите, что если две окружности касаются, то точка касания и центры этих окружностей лежат на одной прямой.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Две окружности касаются внешним образом?
Две окружности касаются внешним образом.
Радиус одной окружности на 3 см меньше радиуса другой окружности.
Найдите диаметры окружностей, если расстояние между их центрами равно 11 см.
Видео:ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

Две окружности касаются внутренним образом?
Две окружности касаются внутренним образом.
Третья окружность касается первых двух и их линии центров.
А) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.
Б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2.
Видео:Касание окружностей | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Каждая из трех окружностей касается двух других?
Каждая из трех окружностей касается двух других.
Зная, что окружности радиуса 3см касаются окружности радиуса 7см внутренним образом, найдите периметр треугольника с вершинами в центрах этих окружностей.
И пожалуйста с тертежом)))Очень срочно на понедельник, ппплллииииииииииииззззз(((.
Видео:Профильный ЕГЭ 2024. Задача 16. Касающиеся окружностиСкачать

В окружность радиуса 16 см на расстоянии 2 см от центра проведена хорда?
В окружность радиуса 16 см на расстоянии 2 см от центра проведена хорда.
В меньший из образовавшихся сегментов помещены две окружности одинакового радиуса так, что они касаются одна другой и каждая из них касается данной окружности и проведенной хорды.
Определить радиус этих двух окружностей.
Видео:Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать

Две окружности касаются внешним образом?
Две окружности касаются внешним образом.
Радиус большей окружности равен 4 см.
Радиус меньшей окружности в 2 раза меньше радиуса большей окружности.
Найдите расстоянии между центрами этих окружностей.
Видео:Решение планиметрических задач повышенного уровня сложностиСкачать
Найдите геометрическое место центров окружностей одного радиуса, касающихся данной окружности внешним образом?
Найдите геометрическое место центров окружностей одного радиуса, касающихся данной окружности внешним образом.
На этой странице находится вопрос Две касающиеся окружности одинакового радиуса 0, 75 находятся внутри третьей окружности и касаются ее так, что диаметры всех этих трех окружностей лежат на одной прямой?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.
Cos A = AC / AB = 8 / 10 = 0, 8.
Для удобства обозначим угол VOY — x, YOU — y ; VOU = x + y = 80° ; ZOX = 2x + 2y = (x + y) + (x + y) = 80 + 80 = 160°.
При пересечении двух прямых получаются две пары одинаковых углов а и в таких, что а + в = 180. Раз сумма равна 50 — значит имеются ввиду противолежащие углы которые равны между собойа + а = 50, стало быть 2а = 50, а = 25 градусов. Угол в = 180 — 25..
Рядом с углом 135° на прямой а находится смежный угол. Сумма их = 180°. Смежный угол = 180 — 135 = 45°. — такой же как между прямыми b и c, значит, прямые а и b — параллельные. Если прямые а и b параллельны, значит угол (2) = 70°. Угол (2) и уго..
Сфотой ещё раз пожалуйста только поближе.
Если плоскости α и β параллельные, то они не могут пересекаться, следовательно и прямые а и b , которые лежат на этих плоскостях, также будут параллельными и не будут пересекаться.
Основные научные достижения арабских ученых относятся ко времени Раннего Средневековья. Значителен был вклад арабов в математическую науку. В VIII в. – и особенно в IX — Х вв. – арабские ученые сделали важные открытия в области геометрии, тригоно..
BD = BC + CD BD = y + x BO = (y + x) / 2 BP = BC + CP = y + 0. 5x PA = PD + DA = 0. 5x — y Естественно вы пишите вверху вектора).
Х — 4о — х = 180 2х — 40 = 180 2х = 140 х = 70 70 — 40 = 30.
💥 Видео
Задача №16. Пересекающиеся и касающиеся окружности.Скачать

11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать

#7str. Как использовать инверсию?Скачать

Одна из самых красивейших задач 19 векаСкачать

Касание окружностей | Задачи 11-15 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

[7] Окружности с нуля для ЕГЭ по математике. Внешнее касание окружностей. Конструкция из демоверсии.Скачать
![[7] Окружности с нуля для ЕГЭ по математике. Внешнее касание окружностей. Конструкция из демоверсии.](https://i.ytimg.com/vi/Ddj3m-1b_G4/0.jpg)
Интенсив СИРОП по математике. Профильный ЕГЭ. Планиметрия. Задача 1Скачать

Построение касательных | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

























