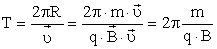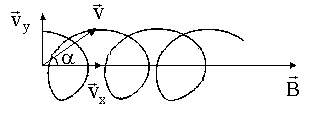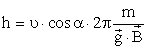Радиус окружности и период обращения частицы по окружности (8 видео)

Движение заряженной частицы в магнитном поле.

Для вывода общих закономерностей движения заряженной частицы в магнитном поле будем считать магнитное поле однородным, электрические поля на частицу не действуют. При этом учтем очевидное:

а) Если заряженная частица движется в магнитном поле вдоль силовой линии, сила Лоренца, действующая на неё, равна нулю

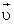
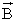
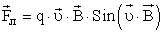
б) Если заряженная частица движется в магнитном поле со скоростью , перпендикулярно к вектору , то сила Лоренца, равная постоянна по модулю и перпендикулярна к траектории частицы.

Согласно второму закону Ньютона, эта сила создаёт центростремительное ускорение. Поэтому частица будет двигаться по окружности, радиус которой определяется из условия:

, , ,

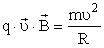
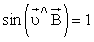
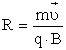
период вращения частицы, т. е. время, затрачиваемое ею на один полный оборот,

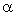
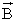
в) Если скорость заряженной частицы направлена под углом к вектору то её движение можно представить в виде двух движений: 1) равномерного прямолинейного движения вдоль поля, 2) равномерного движения по окружности в плоскости перпендикулярной полю (Рис. 23).

В результате этих двух движений возникает движение по винтовой линии, ось которой параллельна вектору 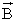. Шаг винтовой линии:

Направление, в котором закручивается частица, зависит от знака её заряда.

Действие магнитного поля на движущиеся заряженные частицы. Действие магнитного поля на проводник с током означает, что магнитное поле действует на движущиеся электрические заряды. Найдем силу, действующую на электрический заряд q при его движении в однородном магнитном поле с индукцией .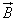
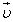
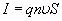
Сила тока I в проводнике связана с концентрацией n свободных заряженных частиц, скоростью их упорядоченного движения и площадью S поперечного сечения проводника следующим выражением:

,(1)

где q — заряд отдельной частицы.

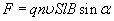
Так как произведение nSl равно числу свободных заряженных частиц в проводнике длиной l

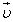
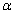
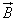
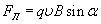
то сила, действующая со стороны магнитного поля на одну заряженную частицу, движущуюся со скоростью под углом к вектору индукции, равна

.(2)

Эту силу называют силой Лоренца.
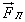
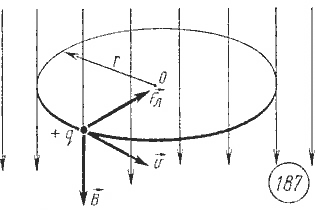
Направление вектора силы Лоренца определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.

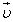
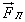
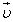
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила , постоянная по модулю и направленная перпендикулярно вектору скорости (рис. 187).

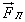
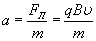
В вакууме под действием силы Лоренца частица приобретает центростремительное ускорение

(3)

и движется по окружности. Радиус r окружности, по которой движется частица, определяется из условия

, .(4)

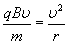
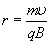
Период обращения частицы в однородном магнитном поле равен

.(5)

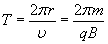
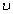
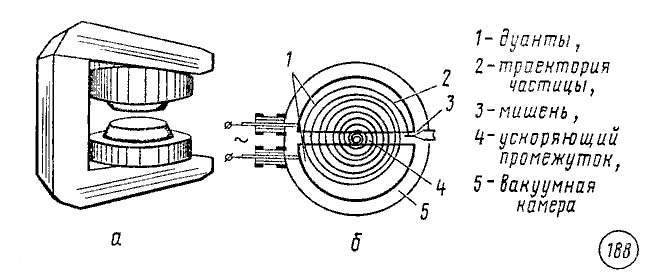
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле при постоянной массе не зависит от скорости и радиуса r траектории ее движения. Этот факт используется, например, в ускорителе заряженных частиц — циклотроне.

Циклотрон. В этом ускорителе заряженные частицы — протоны, ядра атомов гелия — разгоняются переменным электрическим полем постоянной частоты в вакууме в зазоре между двумя металлическими электродами — дуантами. Дуанты находятся между полюсами постоянного электромагнита (рис. 188, а).

Под действием магнитного поля внутри дуантов заряженные частицы движутся по окружности. К моменту времени, когда они совершают половину оборота и подходят к зазору между дуантами, направление вектора напряженности электрического поля между дуантами изменяется на противоположное и частицы вновь испытывают ускорение. Каждую следующую половину оборота частицы пролетают по окружности все большего радиуса (рис. 188, б), но период их обращения остается неизменным. Поэтому для ускорения частиц на дуанты подается переменное напряжение с постоянным периодом.
Ускорение частиц в циклотроне с постоянным периодом возможно лишь до значений скоростей, значительно меньших скорости света. С приближением скорости частицы к скорости света в вакууме, равной c = 300000 км/с, масса частицы возрастает, вследствие чего увеличивается период ее обращения в магнитном поле. Равенство периода обращения частицы и периода изменения электрического поля нарушается, ускорение прекращается.

топлива по сравнению с обычной тепловой электростанцией.

В заключение, по традиции, предлагаем Вашему вниманию шпаргалку по этой теме:

Содержание

I. Механика
Тестирование онлайн
Угловая скорость
Период и частота
Линейная скорость
Центростремительное ускорение
Вращение Земли
Связь со вторым законом Ньютона
Как вывести формулу центростремительного ускорения
Движение по циклоиде*
Радиус окружности и период обращения частицы по окружности
📽️ Видео

Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

I. Механика

Видео:Физика - движение по окружностиСкачать

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:Центростремительное ускорение. 9 класс.Скачать

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Видео:Физика | Равномерное движение по окружностиСкачать

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Видео:Урок 34 (осн). Сила упругости. Закон ГукаСкачать

Радиус окружности и период обращения частицы по окружности

α-частица, кинетическая энергия которой W=500 эВ, влетает в однородное магнитное поле, перпендикулярное к направлению ее движения. Индукция магнитного поля B=0,1 Тл. Найти силу F, действующую на α-частицу, радиус R окружности, по которой движется α-частица, и период обращения Т α-частицы.

Дано:

W=500 эВ = 800·10 -19 Дж

Решение:

На α-частицу, движущуюся в магнитном поле, действует сила Лоренца

Силовая линия вектора В перпендикулярна скорости, т.е.

Скорость найдем, зная кинетическую энергию α-частицы

ила Лоренца является центростремительной

Радиус R окружности, по которой движется α-частица, будет равен