Видео:10.16.1. Планиметрия. Гордин Р.К.Скачать

Ваш ответ
Видео:Геометрия Две окружности пересекаются в точках A и B. Через точку A проведены диаметры AC и AD этихСкачать

решение вопроса
Видео:Геометрия Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второйСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,044
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:ЕГЭ задание 16Скачать

Две окружности пересекаются в точках прямая проходящая через точку
Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точке A, а вторую — в точке D. Прямая, проходящая через точку Q параллельно AD, второй раз пересекает первую окружность в точке B, а вторую — в точке C.
а) Докажите, что четырёхугольник ABCD — параллелограмм.
б) Найдите отношение CP : PB, если радиус первой окружности втрое больше радиуса второй.
а) Обозначим ∠BAD = ∠PAB = α. Поскольку ABQP и CDPQ — вписанные четырёхугольники:
Значит, ∠BAD + ∠ADC = 180°, и поэтому AB || CD. Противоположные стороны четырёхугольника ABCD попарно параллельны, следовательно, это параллелограмм.
б) Пусть R — радиус второй (меньшей) окружности. Тогда радиус большей окружности равен 3R. По теореме синусов:
Ответ : CP : PB = 1 : 3.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Две окружности пересекаются в точках A и B Через точку A проведены диаметры AC и AD этих окружностеСкачать 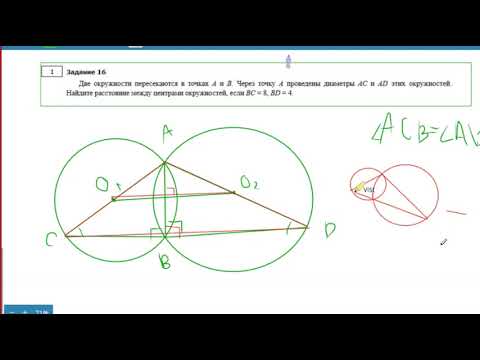 Решение задач по геометрии ЕГЭ №16Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов Сертификат и скидка на обучение каждому участнику ЕГЭ 2017 Вариант №4 (№16) Две окружности пересекаются в точках P и Q . Прямая, проходящая через точку P , второй раз пересекает первую окружность в точке A , а вторую – в точке D . Прямая, проходящая через точку Q параллельно AD , второй раз пересекает первую окружность в точке B , а вторую – в точке C . А) Докажите, что четырёхугольник ABCD – параллелограмм. Б) Найдите отношение BP : PC , если радиус первой окружности вдвое больше радиуса второй. 1.Четырёхугольники ABQP и PDCQ – трапеции (т.к прямые AD ∥ BC по условию). Учитывая, что четырёхугольники вписаны в окружности, следует что они являются равнобедренными т.е. AB = QP и PQ = DC AB = DC . 2.У равнобедреннытрапеций углы при основаниях равны: ∠ BAC + ∠ APQ , ∠ PQC = ∠ QCD , а ∠ APQ = ∠ PQC как накрест лежащие при параллельных прямых AD и BC и секущей PQ , то ∠ BAP = ∠ QCD (по закону транзитивности) зничит ∠ BAP + ∠ ABQ = ∠ QCD + ∠ ABQ = 180 0 . Если сумма односторонних углов при прямых AB и DC и секущей BC равна 180 0 то ( по признаку параллельности прямых) AB ∥ DC . По определению, четырёхугольник у которого противолещащие стороны лежат на параллельных прямых называется параллелограммом. Значит ABCD – параллелограмм, что требовалось доказать. б) Окружности описанные около четырёхугольников ABQP и PDCQ , можно рассмотреть, как окружности описанные около треугольников ∆ BQP и ∆ PCQ . Пусть ∠ BQP =, тогда ∠ PQC = 180 0 — . По формулам приведения sin (180 0 — sin Так как для любого треугольника отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности (следствие из теоремы синусов), то : = (2 R 1 ) : (2 R 2 ) , т.е. = = т.к. по условию радиус первой окружности в два раза больше радиуса второй. ЕГЭ 2017 Вариант №5 (№16) На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE BFKC . Точка M – середина стороны . а)Докажите, что CM = DK б)Найдите расстояние от точки M до центров квадратов, если AC = 6, BC = 10 и ∠ ACB = 30 0 . 1.Проведу луч CM , и на его продолженииотложу отрезок MC 1 = CM . Четырёхугольник AC 1 BC параллелограммм (т.к. диагонали точкой пересечения делятся пополам: медиана по условию) 2. BC = b , AC = a , ∠ ABC = ∠ C 1 BP = ( ∠ ABC = ∠ C 1 BP соответственные углы при параллельных прямых BC 1 и AC и секущей BC ) ∠ С 1 BC = 360 0 — 180 0 — = 180 0 — ∠ KCD = 360 0 — 90 0 — — 90 0 = 180 0 — , т.е. ∠ С 1 BC = ∠ RCD , BC 1 = AC = a = CD , BC = CK = b треугольники ∆ С 1 BC и ∆ KCD равны по второму признаку равенства треугольников KD = C 1 C , MC = CC 1 = KD что и требовалось доказать. б) 1.Рассмотрю треугольник ∆ ABC . По теореме косинусов AB 2 = AC 2 + BC 2 — 2 AC * BC cos 30 0 , AB 2 = 36+100 – 2*6*10 * = 136 — 60, AB =. 2. Рассмотрю ∆ MBO 1 : BO 1 = BK = , MB= cos ∠ O 2 AM = cos( ∠ MAC +45 0 ) =cos45 0 cos ∠ MB -sin 45 0 sin ∠ MBC= (cos ∠ MBC — из ∆ MBC cos ∠ MBC= = = = sin ∠ MBC =, т . к . . MC= 3. Рассмотрю ∆ MAO 2 : AO 2 = AD = , MA cos ∠ O 2 AM= cos( ∠ MAC +45 0 ) =cos45 0 cos ∠ MAC -sin 45 0 sin ∠ MAC= (cos ∠ MAC — из ∆ MAC cos ∠ MAC= = = = ЕГЭ Ларин. Вариант №101 №16 В остроугольном треугольнике АВС высоты АА 1 и СС 1 пересекаются в точке О. А) Докажите, что треугольники АОС и С 1 ОА 1 подобны. Б) Найдите площадь четырехугольника АСА 1 С 1 , если известно, что угол АВС равен 30 о , а площадь треугольника АВС равна 80. 1. Рассмотрю ∆ COA 1 и ∆ AOC 1 . Эти треугольники подобны по первому признаку подобия треугольников (по углам), так как ∠ COA 1 = ∠ AOC 1 — как вертикальные, ∠ OA 1 C = ∠ OC 1 A = 90 0 . Из подобия треугольников ( по определению подобия треугольников) пропорциональность соответствующих сторон: = =. По свойству пропорции из равенства = ⟹ = ( если поменять в верной пропорции крайние) 2. Т.к. = и ∠ AOC = ∠ A 1 OC 1 то треугольники АОС и С 1 ОА 1 подобны по второму признаку подобия треугольников (по пропорциональности двух сторон и равенству углов между этими сторонами). Ч.т.д. б) По условию задачи S ∆ ABC = 80. S ∆ ABC = AB * CC 1 = BC * AA 1 = AB * BC * sin 30 0 . Из ∆ AA 1 B AA 1 = AB , из ∆ CC 1 B CC 1 BC — катеты прямоугольных треугольников лежащих напротив угла в 30 0 , из ∆ AA 1 B BA 1 = BA*cos 30 0 = BA из ∆ CC 1 B BC 1 = BC*cos 30 0 = ⟹ S ∆A1BC1 = A 1 B*BC 1 *sin 30 0 = 🎥 ВидеоПоступайте правильно Математика ЕГЭСкачать 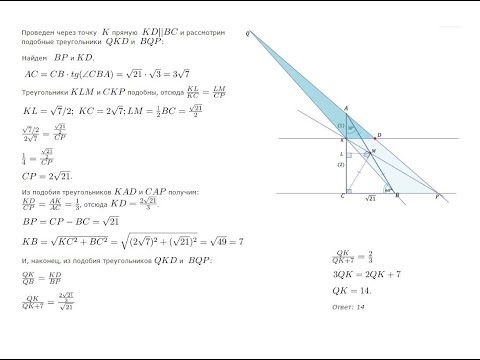 Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Две окружности/ Повторяем углыСкачать  Разбор Задачи №16 из Варианта Ларина №279 (РешуЕГЭ 527391)Скачать  №7. Две прямые пересекаются в точке М. Докажите, что все прямые, не проходящие через точкуСкачать  Через точку A, лежащую вне окружности, проведены две прямые.Скачать  Две окружности пересекаются, если радиус одной ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать  Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Планиметрия. №6. (16 задача ЕГЭ).Скачать  ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать  Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать  Задание 26 Две окружности, внешнее касаниеСкачать  Задание 16 ЕГЭ по математикеСкачать  |


