Две окружности пересекаются в точках а и в так

Условие

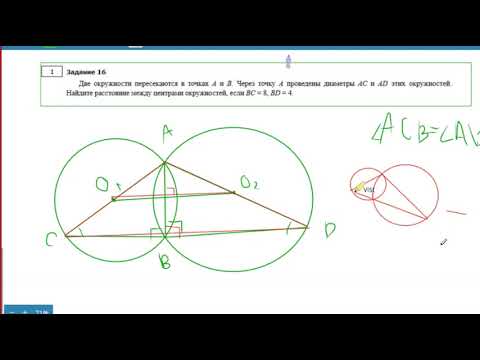
Две окружности пересекаются в точках А и В. Из точки С, лежащей на продолжении отрезка АВ за точку В, проведены касательная СК к первой окружности, не пересекающая
вторую окружность, и касательная СТ ко второй окружности, не пересекающая первую окружность (К и Т — точки касания). Прямая, проходящая через центры окружностей, пересекает дугу АКB первой окружности в точке Р, а дугу АТВ второй окружности — в точке Н.

а) Докажите, что СТ = СК.

б) Найдите длину отрезка КТ, если СТ = 1, а сумма дуг КР и ТН равна 60°. [16п1]

Решение

[red]a)[/red]
Из точки А к каждой окружности проведены[i] касательная[/i] и [i]секущая[/i].
По свойству касательной и секущей, проведенных к окружности из одной точки:
CK^2=CB*CA и СT^2=CB*CA
Правые части равны, значит CK^2=CT^2 ⇒ [b]CK=CT[/b]

[red]б)[/red]
СТ=1; ∪ KP+ ∪ TH = 60 °
Найти KT
∠ PO_(1)K и ∠ TO_(2)H — [i]центральные[/i], они измеряются величиной дуги, на которую опираются

∠ PO_(1)K+ ∠ TO_(2)H = 60 °

В четырехугольнике СКО_(1)В
∠ СКО_(1)=90 ° и СМО_(1)=90 °
Значит,
∠ КО_(1)B + ∠ KCB=180 °
∠ КО_(1)B — смежный с ∠ PO_(1)K
∠ KCB=∠ PO_(1)K

Аналогично, из четырехугольника СМО_(2)Т
∠ ВСТ= ∠ TO_(2)H

∠ KCB+ ∠ ВСТ= ∠ PO_(1)K+∠ TO_(2)H=60 ° ⇒
[b] ∠ КСТ=60 ° [/b]

Δ СКТ равнобедренный, угол при вершине 60 ° ; значит это равносторонний треугольник и КТ=1

Видео:Геометрия Две окружности пересекаются в точках A и B. Через точку A проведены диаметры AC и AD этихСкачать

Две окружности пересекаются в точках А и В. На продолжении их общей хорды АВ выбрана точка М. Из этой точки проведены касательные ME

Видео:Геометрия Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второйСкачать

Ваш ответ

Видео:Две окружности пересекаются в точках A и B Через точку A проведены диаметры AC и AD этих окружностеСкачать

решение вопроса

Видео:Планиметрия 11 |mathus.ru|  расстояние между центрами пересекающихся окружностейСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,036
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°, ∪BC= 70°.Скачать

. Две окружности пересекаются в точках A и B?

Геометрия | 5 — 9 классы

. Две окружности пересекаются в точках A и B.

Точка X лежит на прямой AB, но не на отрезке AB.

Докажите, что длины всех касательных, проведенных из точки Xк окружностям, равны.

Для удобства описания решения позволю себе обозначить O как O2, F как F1 и E как F2.

Обозначим точку пересечения AB и O1 O2 как D.

Решение будет симметрично относительно прямой AB, поэтому индексы я опускаю.

Рассматриваем треугольник OBD : угол D прямой.

Значит, OD ^ 2 = OB ^ 2 — BD ^ 2.

Рассматриваем треугольник OMD : угол D прямой, значит, OM ^ 2 = OD ^ 2 + MD ^ 2 = OB ^ 2 — BD ^ 2 + MD ^ 2.

Рассматриваем треугольник OMF : угол F прямой, значит, MF ^ 2 = OM ^ 2 — OF ^ 2 = OB ^ 2 — BD ^ 2 + MD ^ 2 — OF ^ 2.

Вспоминаем, что OB = OF = R — радиус окружности, поэтому, MF ^ 2 = MD ^ 2 — BD ^ 2.

Равенство справедливо как для первой окружности, так и для второй.

Осталось подставить соответствующие индексы.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Докажите, что касательная к окружности перпендикулярна к радиусу этой окружности, проведенному в точку касания?

Докажите, что касательная к окружности перпендикулярна к радиусу этой окружности, проведенному в точку касания.

Видео:Две окружности пересекаются, если радиус одной ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Две окружности касаются друг друга внешним образом в точке А?

Две окружности касаются друг друга внешним образом в точке А.

Прямая, проходящая через точку А, пересекает первую окружность в точке В, а вторую в точке С.

Касательная к первой окружности, проходящая через точку В, пересекает вторую окружность в точках Д и Е.

(Д лежит между В и Е).

Известно, что АВ = 5 и АС = 4.

Видео:ОГЭ Задание 25 Две окружностиСкачать

Отрезки AB и AC являются отрезками касательных к окружности с центром O, проведенными из точки A?

Отрезки AB и AC являются отрезками касательных к окружности с центром O, проведенными из точки A.

Найдите угол BAC, если середина отрезка AO лежит на окружности.

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Две окружности, расстояние между центрами которых равно 21, а радиусы равны 10 и 17, пересекаются в точках P и Q?

Две окружности, расстояние между центрами которых равно 21, а радиусы равны 10 и 17, пересекаются в точках P и Q.

В точкеP проведена касательная к большей из этих окружностей, а в точке Q проведена касательная к меньшей из окружностей.

Проведенные касательные пересекаются в точке K.

Найдите площадь треугольника KPQ.

Видео:№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

Отрезок AB является диаметром окружности с центром в точке О?

Отрезок AB является диаметром окружности с центром в точке О.

В точках А и В проведены касательные к окружности.

Через центр окружности проведена прямая, которая пересекает касательные в точках C и D.

Докажите, что длины отрезков OC и OD равны.

Заранее огромное спасибо♥.

Видео:Две окружности/ Повторяем углыСкачать

Дана окружность с центром в точке O?

Дана окружность с центром в точке O.

Через точку A, расположенную вне окружности, и точку O проведена прямая, пересекающая окружность в точках P и Q.

Найдите длину касательной AB, проведенной к данной окружность, если AP = 4, AQ = 9.

Видео:Планиметрия. №6. (16 задача ЕГЭ).Скачать

Докажите , что отрезки касательных к окружности , проведённые из одной точки, равны и составляют равные углы с прямой , проходящей через эту точку и центр окружности?

Докажите , что отрезки касательных к окружности , проведённые из одной точки, равны и составляют равные углы с прямой , проходящей через эту точку и центр окружности.

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Тяжелая планиметрия, помогите, пожалуйста?

Тяжелая планиметрия, помогите, пожалуйста.

Две окружности внешне касаются друг друга в точке A.

Общая внешняя касательная касается первой окружности в точке B, второй – в точке C.

Прямая BA пересекает вторую окружность в точке D, при этом AB = 5 и AD = 4 .

Найти длину отрезка AC и радиусы окружностей.

Видео:№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать

Две прямые, касающиеся данной окружности в точках А и В, пересекаются в точке С?

Две прямые, касающиеся данной окружности в точках А и В, пересекаются в точке С.

Докажите, что центр окружности, вписанной в треугольник АВС, лежит на данной окружности.

Видео:Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Точки А и С лежат на окружности?

Точки А и С лежат на окружности.

Касательные к окружности, проведенные через эти точки, пересекаются в точке В, АС = АВ.

Докажите, что биссектриса угла АСВ пройдет через середину отрезка АВ.

Перед вами страница с вопросом . Две окружности пересекаются в точках A и B?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

3 угол равен 9 * Т. К сумма острых углов прямоугольного треугольника равна 90 * То угол 3 = 90 — 81 = 9 *.

В треугольнике может быть только один тупой угол и против него лежит большая сторона, равная 3. По теореме о неравенстве треугольника большая сторона должна быть МЕНЬШЕ суммы двух других сторон. Значит третья сторона треугольника должна быть 2.

Рассмотрим треугольники АОD и ВОС 1. ∠ADO = ∠CBOкак внутр накрест лежащие 2. ∠DAO = ∠BCO как внутр накрест лежащие 3. AD = BC противолеж стороны паралл (след треугольники равны, по двум углам и стороне между ними) соответств стороны равны AO = CO.

Пусть ABCD – данный четырехугольник. По условию AO = OC, BO = OD. Так как углы (AOB) и (COD) равны как вертикальные, то по теореме 4. 1 треугольник AOB равен треугольнику COD, и, следовательно, углы (OAB) и (OCD) равны. Эти углы являются внутренн..

Параллелограмм состоит из двух одинаковых треугольников со сторонами 15, 17, 18 Площадь одного такого треугольника найдём по формуле Герона Полупериметр p = (15 + 17 + 18) / 2 = 50 / 2 = 25 S = √(25 * 10 * 8 * 7) = 5 * 4√35 = 20√35 Площадь всего пар..

Как — то так, а четвертое, незнаю.

Во — первых, геометрия знакомит нас с окружающей действительностью, в которой многие предметы напоминают различные геометрические фигуры, фактически мы живем в мире геометрии. Во — вторых в равной степени геометрия нужна и математику, и инженеру, и ..

1. Фронтально — проецирующая плоскость 2. Горизонтально — проецирующая плоскость 3. Профильно — проецирующая плоскость 4. Фронтальная плоскость уровня 5. Горизонтальная плоскость уровня 6. Профильная плоскость уровня.

📺 Видео

ЕГЭ Задание 16 Две касающиеся окружностиСкачать

На рис. изображены графики f(x)=2x^2-5x+4 и g(x)=ax^2+bx+c, кот. пересекаются в точках А и В.Скачать

Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

№666. Хорды АВ и CD пересекаются в точке Е. Найдите ED, если: а) АЕ = 5, ВЕСкачать