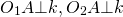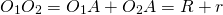ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.
§ 74. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ОКРУЖНОСТЕЙ.
Прямая, проходящая через центры двух окружностей, называется линией центров.
Рассмотрим взаимное расположение двух окружностей.
1.Окружности не имеют общей точки.
а) Окружности лежат одна вне другой.
В этом случае расстояние между центрами больше суммы радиусов: OO’ > R + r (черт. 322).
б) Одна окружность лежит внутри другой.
В этом случае расстояние между центрами меньше разности радиусов: OO’ R — r (§ 16).
Справедливы и обратные предложения:
1) если OO’ > R + r или OO’ R — r , то окружности пересекаются.
Все предложения, изложенные в § 74, даны без доказательства. Они могут быть строго доказаны, как и другие предложения.
Окружности, имеющие общий центр, называются концентрическими. При равных радиусах они совмещаются, при различных радиусах — не имеют ни одной общей точки (черт. 327).
Видео:№13. Могут ли две плоскости иметь: а) только одну общую точку; б) только две общие точкиСкачать

Окружность. Относительное взаимоположение окружностей.
Если две окружности имеют только одну общую точку, то говорят, что они касаются.
Если же две окружности имеют две общие точки, то говорят, что они пересекаются.
Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.
Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).
Теорема.
Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.
Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.
Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.
Следствие.
Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.
Теоремы.
1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.
2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.
Признаки различных случаев относительного положения окружностей.
Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.
Эти окружности могут находиться в следующих 5-ти относительных положениях:
1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .
2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.
3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.
4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.
5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,
d R + R1, то окружности расположены одна вне другой, не касаясь.
2. Если d = R + R1, то окружности касаются извне.
3. Если d R — R1, то окружности пересекаются.
4. Если d = R — R1, то окружности касаются изнутри.
5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.
Видео:Взаимное расположение окружностей. 7 класс.Скачать

Касание двух окружностей
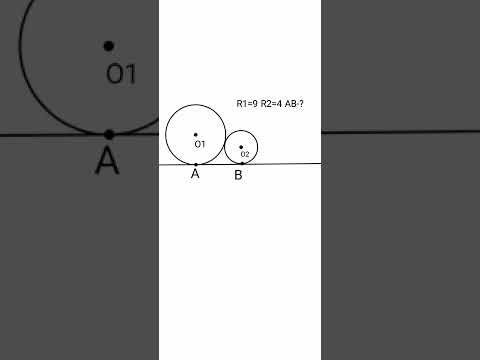
Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.
Общая точка двух окружностей называется точкой касания окружностей.
Касание окружностей может быть внешним и внутренним.
Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной.
Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной.
Касающиеся окружности имеют только одну общую точку — точку касания.
Центры касающихся окружностей и их общая точка касания лежат на одной прямой.
При любом виде касания по свойству касательной касательная перпендикулярна радиусам, проведённым в точку касания:
По теореме о существовании и единственности прямой, перпендикулярной данной,через точку A можно провести только одну прямую, перпендикулярную данной прямой k.
Следовательно, все три точки: центры окружностей O1, O2 и A лежат на одной прямой.
Что и требовалось доказать .
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
При внутреннем касании расстояние между центрами окружностей равно разности радиусов:
🔍 Видео
Геометрия Две окружности имеют единственную общую точку M. Через точку M проведены две прямыеСкачать

Две окружности на плоскости. Математика. 6 класс.Скачать

Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

ОГЭ Задание 25 Две окружностиСкачать

Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать

Две окружности #shortsСкачать
28 ноября две окружностиСкачать

Касание окружностейСкачать

При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку?Скачать

Две окружности/ Повторяем углыСкачать

✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать

Геометрия. 7 класс. Взаимное расположение двух окружностей /15.04.2021/Скачать

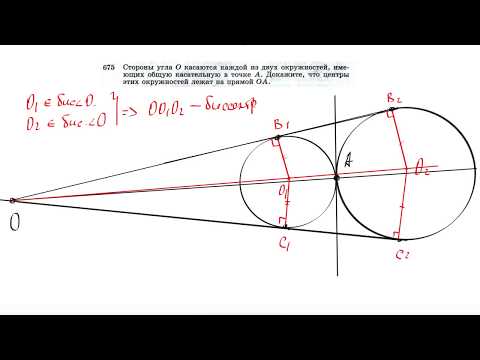
№675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке АСкачать
8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

7 класс. Геометрия. Взаимное расположение двух окружностей.Скачать

7 класс. Геометрия. Взаимное расположение двух окружностей. 28.04.2020.Скачать

Геометрия. Задача. Окружности.Скачать