Два перпендикуляра к одной прямой параллельны верно или нет (7 видео)

Геометрия. 10 класс

Содержание

Лекция по геометрии на тему: «Перпендикулярность в пространстве». 10-й класс
Перпендикулярность прямых и плоскостей
Перпендикулярные прямые
Перпендикулярность прямой и плоскости
Признак перпендикулярности прямой и плоскости
Свойства перпендикулярных прямой и плоскости
Перпендикулярность плоскостей
Признак перпендикулярности плоскостей
Свойство перпендикулярных плоскостей
🎦 Видео

Конспект урока

Геометрия, 10 класс

Урок № 8 Перпендикулярность прямой и плоскости

Перечень вопросов, рассматриваемых по теме

Ввести понятие перпендикулярных прямых в пространстве;
Доказать лемму о перпендикулярности двух параллельных прямых;
Решать задачи по теме.

Глоссарий по теме

Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости

Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 9 класса. Базовый и профильный уровень

Зив Б.Г. Геометрия. Дидактические материалы. 10-11 класс М.: Просвещение, 2015.

Открытые электронные ресурсы:

Перпендикулярность прямой и плоскости. http://school-collection.edu.ru // Единая коллекция цифровых образовательных ресурсов.

Перпендикулярность прямой и плоскости. https://www.yaklass.ru // Я-класс. Образовательный портал Сколково.

Теоретический материал для самостоятельного изучения

Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как а ⊥ с, то ∠АМС=90 о .

Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между ними равен 90 о , т.е. b ‖ МА, с ‖ МС, угол между МА и МС равен 90 о

Это означает, что угол между прямыми b и с также равен 90 о , то есть b ⊥ с.

Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.

По лемме о перпендикулярности двух параллельных прямых к третьей а₁ ⊥ x.

Таким образом, прямая а₁ перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а₁ ⊥ α

Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.

Через какую-нибудь точку М прямой b проведем прямую b₁, параллельную прямой а.

Докажем, что прямая b₁ совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b₁ и b не совпадают. Тогда в плоскости β, содержащей прямые b и b₁, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b₁ ∊ β, α β = c (невозможно)→ а ‖ b

Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.

Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.

В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.

Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.

Предположим, что существует прямая с₁, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с₁ перпендикулярны плоскости α. Значит, прямые с и с₁ параллельны. Но по построению прямые с и с₁пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.

Теоретический материал для углубленного изучения

Доказательство (см. рис. 1)

Пусть нам дана прямая а и точка М. Докажем, что существует плоскость γ, которая проходит через точку М и которая перпендикулярна прямой а.

Через прямую а проведем плоскости α и β так, что точка М принадлежит плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, . В плоскости β из точки N восстановим перпендикуляр q к прямой а. Прямые р и q пересекаются, пусть через них проходит плоскость γ. Получаем, что прямая а перпендикулярна двум пересекающимся прямым р и q из плоскости γ. Значит, по признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости γ.

Примеры и разборы решения заданий тренировочного модуля

Выбор элемента из выпадающего списка

Выпишите ребра, перпендикулярные плоскости (DC).

Правильный вариант/варианты (или правильные комбинации вариантов):

Неправильный вариант/варианты (или комбинации):

Подсказка: в кубе все углы по . Плоскость (DC), проходит через грань куба DC.

Разбор задания: Куб – это геометрическая фигура у которой все углы прямые, следовательно нужно увидеть ребра которые перпендикулярны к плоскости (DC), к грани куба (DDC).Эти ребра — AD, A₁D₁, BC, B₁C₁

Закончите предложение, чтобы получилось верное утверждение.

Две прямые называются перпендикулярными, если …..
Если плоскости перпендикулярна одной из двух параллельных прямых, то она ……

параллельны
один
она перпендикулярна к любой прямой, лежай в этой плоскости.
перпендикулярна плоскости.

Правильный вариант/варианты (или правильные комбинации вариантов):

Две прямые называются перпендикулярными, если …

угол между ними равен 90

Если плоскость перпендикулярна одной из двух параллельных прямых, то она …

перпендикулярна и другой

Неправильный вариант/варианты (или комбинации):

Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.

Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Лекция по геометрии на тему: «Перпендикулярность в пространстве». 10-й класс

Разделы: Математика

Класс: 10

Тема: Перпендикулярность прямой и плоскости.

Определение: Две прямые в пространстве могут пересекаться. (Привести примеры перпендикулярных прямых, используя окружающую обстановку).

Лемма: Если одна из двух прямых перпендикулярна к третьей прямой, то другая прямая перпендикулярна к этой прямой.

Дано: a || b, a c

Доказать: b c

Через т.М | М a, М b и М c проведем прямые MA || a и MC || c. Так как a c (по условию), то АМС =90 0 . По условию a || b и MA || a (по построению) значит, b || MA (по теореме о трех параллельных прямых). Тогда прямые b и c параллельны соответственно МА и МС, угол между которыми 90 0 b c, что и требовалось доказать.

Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

(Возможна запись: a или a).

Прямая, перпендикулярная к плоскости пересекает эту плоскость.

a a b, a c, a d.

Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая также перпендикулярна к этой плоскости.

Дано: a || b, a .

Доказать: b .

Проведем в плоскости произвольную прямую с. Так как a , то a с (по определению). Согласно лемме, если а перпендикулярна с, то и b, параллельная а также перпендикулярна с. Так как с – произвольная прямая, то b перпендикулярна . (по определению). Что и требовалось доказать.

Теорема (обратная): Если 2 прямые перпендикулярны к плоскости, то они параллельны.

(Доказать предлагается учащимся самостоятельно).

Теорема: Если прямая, не лежащая в плоскости перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то прямая и плоскость перпендикулярны.

Предлагается 2 способа доказательства.

Дано: a , b, c, b x c=0, a b, a c

Доказать: a .

Проведем в плоскости произвольную прямую р. (Если р не проходит через т.О, то можно провести р | || р через т.О) На прямых a, b, c, и p’ отложим векторы , , и соответственно. Так как , и , то =x+y (известно из курса планиметрии). Так как a b, то · =0; так как a c , то ·=0. Докажем, что . Найдем их скалярное произведение ·= ( x+y)=x·+y·=0 a p. Так как p произвольная прямая плоскости , то a (по определению). Что и требовалось доказать.

Дано: m, n, m x n=0, l m, l n

Доказать: l .

Проведем прямую p так, чтобы O p и p || l. l m, l n и p || l p n и p m. Пусть P и P₁ – точки прямой p такие, что OP=OP₁. Тогда m и n –оси симметрии и значит, — плоскость симметрии для этих точек, а следовательно, p . p и p || l l . Что и требовалось доказать.

Замечание: Еще одно доказательство теоремы в учебнике “Геометрия 10-11” Л.С. Атанасяна и др.

Свойства перпендикулярных прямой и плоскости:

Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.

Если две плоскости

Два перпендикуляра к одной прямой параллельны верно или нет

перпендикулярны к прямой а ,то они параллельны.

Если одна из двух параллельных плоскостей перпендикулярна к прямой, то и другая плоскость перпендикулярна к этой прямой.

Теорема: Через любую точку пространства не принадлежащую плоскости проходит прямая перпендикулярная к данной плоскости, и притом только одна.

Дано: , А .

Доказать: a | A a, a .

Доказательство:

Проведем в произвольную прямую а; построим плоскость а, проходящую через т.А =b В плоскости через А проведем прямую с | c (c b по построению c а, т.к. ). Значит, с и есть искомая прямая.
Докажем, что она единственная. Допустим, что это не так и существует прямая с₁, тогда с || c₁ ,что не возможно т.к. с х с₁=А. Таким образом, через А проходит только одна прямая к

. Что и требовалось доказать

Можно предложить учащимся подготовить к семинару ответы на следующие вопросы:

Верно ли что: если 2 прямые в пространстве перпендикулярны к третьей прямой, то это утверждение при условии, что все три прямые параллельны? Верно ли это утверждение при условии, что все три прямые лежат в одной плоскости?

Прямая а ||

, а b

. Существует ли прямая перпендикулярная к прямым а и b?

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Перпендикулярность прямых и плоскостей

Видео:Теорема о двух перпендикулярах к одной прямойСкачать

Перпендикулярные прямые

Две прямые в пространстве называются перпендикулярными , если угол между ними составляет .

При этом прямые могут пересекаться,

а могут быть скрещивающимися:

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Перпендикулярность прямой и плоскости

Прямая называется перпендикулярной к плоскости , если она перпендикулярна любой прямой, лежащей в этой плоскости.

Признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Свойства перпендикулярных прямой и плоскости

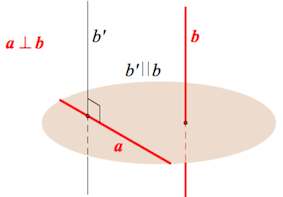
1). Две прямые, перпендикулярные одной и той же плоскости, параллельны.

2). Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.

3). Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой

Видео:7 класс, 16 урок, Перпендикуляр к прямойСкачать

Перпендикулярность плоскостей

Пересекающиеся плоскости называются перпендикулярными , если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Признак перпендикулярности плоскостей

Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Свойство перпендикулярных плоскостей

Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости.