Доклад по теме параллельные прямые (5 видео)

Доклад по теме параллельные прямые

Параллельные прямые — две прямые, которые лежат в одной плоскости и не пересекаются, а || b.

Слово «параллельный» от греческого «parallelos» — идущий рядом. Знак параллельности || впервые встречается в трудах У. Оутреда (1677 г).

Аксиома параллельности:
Через точку, не лежащую на данной прямой, на плоскости можно провести только одну прямую , параллельную данной прямой.

Выделенная синим цветом часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского. В геометрии Лобачевского через точку, лежащую за прямой, проходит множество прямых, которые не пересекают данную прямую.

Иногда Аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.

Примечание. В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Содержание

Свойства и признаки параллельных прямых
Параллельные прямые
Понятие параллельных прямых
Готовые работы на аналогичную тему
Историческая справка
Параллельные прямые в жизни
Параллельные прямые в архитектуре
Проект по теме «Параллельные прямые».
Скачать:
Предварительный просмотр:
Подписи к слайдам:
🎦 Видео

Свойства и признаки параллельных прямых

Свойства и признаки параллельных прямых:

Две прямые, параллельные третьей, параллельны.
Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Если две параллельные прямые пересечены секущей, то:
– сумма внутренних односторонних углов равна 180°,
– накрест лежащие углы равны,
– соответственные углы равны,

Теорема Фалеса:
Если на одной из двух прямых отложено несколько равных отрезков и через их концы проведены параллельные прямые, не пересекающие другую прямую, то и на ней отложатся равные отрезки.

Это конспект по теме «Параллельные прямые». Выберите дальнейшие действия:

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямые

Вы будете перенаправлены на Автор24

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Понятие параллельных прямых

Параллельные прямые – прямые, которые лежат в одной плоскости, не совпадают и не имеют общих точек.

Если у прямых есть общая точка, тогда они пересекаются.

Если все точки прямых совпадают, то имеем по сути одну прямую.

Если прямые лежат в разных плоскостях, то условий их параллельности несколько больше.

При рассмотрении прямых на одной плоскости можно дать следующее определение:

Две прямые на плоскости называют параллельными, если они не пересекаются.

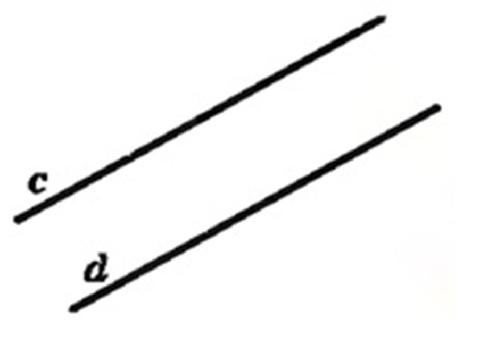
В математике параллельные прямые принято обозначать с помощью знака параллельности « $parallel$ ». Например, тот факт, что прямая $c$ параллельна прямой $d$ обозначается следующим образом:

Зачастую рассматривается понятие параллельных отрезков.

Два отрезка называют параллельными, если они лежат на параллельных прямых.

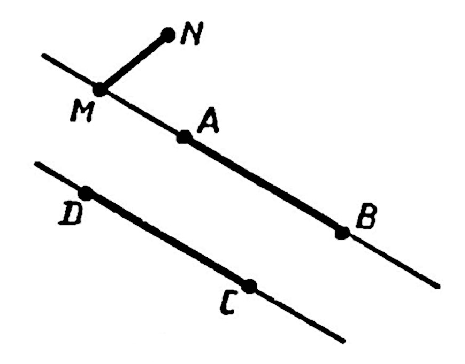
Например, на рисунке параллельными являются отрезки $AB$ и $CD$, т.к. они принадлежат параллельным прямым:

Вместе с тем, отрезки $MN$ и $AB$ или $МN$ и $CD$ параллельными не являются. Этот факт можно записать с помощью символов следующим образом:

Готовые работы на аналогичную тему

$MN ∦ AB$ и $MN ∦ CD$.

Аналогичным образом определяется параллельность прямой и отрезка, прямой и луча, отрезка и луча или двух лучей.

Видео:Параллельные прямые. 6 класс.Скачать

Историческая справка

С греческого языка понятие «параллелос» переводится «рядом идущий» или «проведенный друг возле друга». Этот термин использовался в древней школе Пифагора еще до того, как параллельные прямые получили свое определение. Согласно историческим фактам Евклидом в $III$ в. до н.э. в его трудах все же был раскрыт смысл понятия параллельных прямых.

В древности знак для обозначения параллельных прямых имел отличный вид того, что мы используем в современной математике. Например, древнегреческим математиком Паппом в $III$ в. н.э. параллельность обозначалась с помощью знака равенства. Т.е. тот факт, что прямая $l$ параллельна прямой $m$ ранее обозначался «$l=m$». Позднее для обозначения параллельности прямых стали использовать привычный нам знак «$parallel$, а знак равенства стали использовать для обозначения равенства чисел и выражений.

Видео:Контрольная работа по теме: "Параллельные прямые" | Геометрия 7 классСкачать

Параллельные прямые в жизни

Зачастую мы не замечаем, что в обычной жизни нас окружает огромное число параллельных прямых. Например, в нотной тетради и сборнике песен с нотами нотный стан выполнен с помощью параллельных линий. Также параллельные линии встречаются и в музыкальных инструментах (например, струны арфы, гитары, клавиши фортепиано и т.п.).

Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно. Рельсы линий метро и железных дорог располагаются параллельно.

Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий.

Видео:Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

Параллельные прямые в архитектуре

На представленных изображениях архитектурные сооружения содержат параллельные прямые. Использование параллельности прямых в строительстве помогает увеличить срок службы таких сооружений и придает им необычайную красоту, привлекательность и величие. Линии электропередач также умышленно проводятся параллельно, чтобы избежать их пересечения или соприкосновения, что привело бы к замыканию, перебоям и отсутствию электричества. Чтобы поезд мог беспрепятственно перемещаться рельсы также выполнены параллельными линиями.

В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.

Видео:Параллельные прямые (задачи).Скачать

Проект по теме «Параллельные прямые».

Ученица 7 класса проводит исследовательскую работу о параллельных прямых. В ходе работы изучает историю возникновения параллельных прямых, применение их в жизне и рассматривает две точки зрения об аксиоме параллельных прямых Евклида и Лобачевского.

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Скачать:

Вложение	Размер
zashch._slovo.doc	37.5 КБ
paral._proekt.ppt	612 КБ

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Предварительный просмотр:

Тема моего проекта: «Параллельные прямые».

Цель : показать необходимость и значимость параллельных прямых.

Задачи: 1. Изучить историю возникновения параллельных прямых.

2. Рассмотреть применение параллельных прямых в жизни.

3. Сделать сравнительный анализ аксиомы параллельных прямых Евклида и Лобачевского.

Без параллельных прямых невозможна наша жизнь!

Для решения поставленных задач и проверки исходных положений применяются следующие методы исследования: анализ научной литературы; наблюдения, беседы, тесты.

На уроках геометрии мало времени дается на изучение параллельных прямых. Отсюда возникает проблема — недостаток информации по теме «параллельные прямые» в школьном курсе математики.

В жизни мы часто встречаемся с понятиями параллельные прямые.

Название параллельных прямых произошло от греческого слова «параллелой», которое означает «рядом идущие».

Рассмотрим разные определения параллельных прямых Евклида и Посидония. А теперь то современное определение, которое используем мы.

Для обозначения параллельности двух прямых древнегреческие математики использовали знак «=». Однако когда в 18в. этот знак стал использоваться как знак равенства, параллельность стали обозначать с помощью знака «//». И если прямые а и в параллельны, то мы будем записывать это так: а//в.

Мы привыкли слышать и видеть, что параллельные прямые никогда не пересекаются!

Действительно ли невозможно пересечение параллельных прямых?

Быть может существует точка пересечения параллельных прямых?

Попытаемся ответить на эти вопросы.

В жизни мы часто встречаемся с понятием параллельности.

При строительстве зданий строго учитывается понятие параллельности.

Самый наглядный пример параллельности прямых — железнодорожное полотно.

Еще одним примером применения понятия параллельных прямых, является эскалатор.

Все эти устройства помогают нам в повседневной жизни. Если бы не было параллельных прямых, то например, произошло крушение поезда или замыкание проводов и нет электричества. Но свойства параллельных прямых используется гораздо шире.

Но с другой стороны мы столкнулись со странным явлением: устремляя взгляд далеко в бесконечность, можно увидеть пересечение параллельных прямых!

В чем же дело? Чтобы ответить на этот вопрос обратимся к великим ученым.

Но сначала мы обратились к учащимся 7 класса. С ними провели эксперимент «Иллюзии зрения». Учащимся задали вопрос: везде ли на картинках параллельные прямые? Результаты опроса таковы: участвовали 20 человек из них: 11 – 55% считают параллельно, 9 -45% нет.

Вывод: в геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на наблюдения.

Положительный момент: благодаря зрительным искажениям существует живопись.

При изучении геометрии мы опираемся на ряд аксиом. Аксиомы – это положения, которые применяются в качестве исходных. В развитии геометрии важную роль сыграла аксиома, которая в «Началах» Евклида называлась пятым постулатом.

Многие математики, начиная с древних времен, предпринимали попытки доказать пятый постулат Евклида используя другие аксиомы. Однако эти попытки каждый раз оказывались неудачными.

И стояла геометрия Евклида,

Как египетская чудо-пирамида.

Строже выдумать строение невозможно,

Лишь одна была в ней глыба ненадёжна.

Аксиома называлась «параллели».

Разгадать её загадку не сумели.

В конце 18в. у некоторых ученых возникла мысль о невозможности доказать пятый постулат. Огромную роль в решении этого непростого вопроса сыграл великий русский математик Николай Иванович Лобачевский.

И подумал Лобачевский:

« Но ведь связана с природой аксиома!

Мы природу понимаем по-земному.

Во Вселенной расстоянья неземные,

Могут действовать законы там иные!

Параллельные пойдут непараллельно!

Там, где звёздный мир раскинулся без края, —

Аксиома параллели — там другая!».

И Евклид и Лобачевский говорят об одном и том же: о параллельных прямых. Но у одного из них параллельные прямые не пересекаются, а другой говорит о существовании точки пересечения параллельных прямых.

И оба они по своему правы!

Евклид рассматривает параллельность на плоскости .

Лобачевский видит плоскость в пространстве (именно поэтому его геометрию называют воображаемой).

Изучив вопросы по данной теме мы пришли к выводам:

каждый разносторонне развитый ученик должен знать историю параллельных прямых
параллельные прямые часто встречаются в окружающем нас мире, поэтому они очень нужны.
параллельные прямые не пересекаются на плоскости!
в пространстве параллельность прямых исчезает – существует точка пересечения параллельных прямых !

Несмотря на все кажущиеся странности, геометрия Лобачевского является настоящей геометрией нашего мира, и Евклидова является только её составной частью. Но в пределах ежедневных измерений Евклидова геометрия дает ничтожно малые ошибки, и мы пользуемся именно ею.

Хочу закончить свое выступление такими словами: «Было бы легче остановить Солнце, легче сдвинуть Землю, чем свести параллели к схождению…».

Таким образом, цель достигнута, задачи решены.

Спасибо за внимание.

Предварительный просмотр:

Видео:7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Подписи к слайдам:

параллельные прямые Над проектом работала: Прилепова Юлия Под руководством учителя математики Прилеповой О.А.

Цель: Показать необходимость и значимость параллельных прямых

задачи: Изучить историю возникновения параллельных прямых Рассмотреть применение параллельных прямых в жизни. Сделать сравнительный анализ аксиомы параллельных прямых Евклида и Лобачевского.

Гипотеза Без параллельных прямых невозможна наша жизнь!

Проблема Недостаток информации по теме «параллельные прямые» в школьном курсе математики

немного из истории. «параллелой»- “ рядом идущие ” «друг подле друга проведенные» (перевод с греческого языка)

разные определения параллельных прямых. « Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченно, ни с той, ни с другой стороны между собой не встречаются.» Евклид (в lll в. до н. э.)

разные определения параллельных прямых. «Две прямые, лежащие в одной плоскости и равностоящие друг от друга.» Посидоний ( I в. до н.э. )

Параллельные прямые -это прямые, лежащие в одной плоскости и не пересекающиеся. Современное Определение

a b a b a=b У. Оутред ( 1575-1660 ) Папп ( III в. н. э. )

При строительстве зданий строго учитывается понятие параллельности Самый наглядный пример параллельности прямых — железнодорожное полотно

Если бы не было параллельных прямых. замыкание, нет электричества крушение поезда

Но с другой стороны мы столкнулись со странным явлением: устремляя взгляд далеко в бесконечность, можно увидеть пересечение параллельных прямых! В чем же дело? Чтобы ответить на этот вопрос обратимся к великим ученым.

Эксперимент «Иллюзии зрения» ИТОГИ опроса: всего параллельно нет 20 55% 45% Ответ: параллельно. В геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на наблюдения. Положительный момент: благодаря зрительным искажениям существует живопись.

Аксиома параллельных прямых Через точку не лежащую на прямой, можно провести только одну прямую параллельной данной. Пятый постулат Евклида. «Начала»

Евклид ( III век до н . э . ) Древнегреческий математик, автор первого трактата по геометрии «Начала» (в 13 книгах). И стояла геометрия Евклида, Как египетская чудо-пирамида. Строже выдумать строение невозможно, Лишь одна была в ней глыба ненадёжна. Аксиома называлась «параллели». Разгадать её загадку не сумели.

Николай Иванович Лобачевский (1792 – 1856 гг.) И подумал Лобачевский: « Но ведь связана с природой аксиома! Мы природу понимаем по-земному. Во Вселенной расстоянья неземные, Могут действовать законы там иные! Параллельные пойдут непараллельно! Там, где звёздный мир раскинулся без края, — Аксиома параллели — там другая!».

«Чем отличается геометрия Лобачевского от геометрии Евклида?» через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Евклидова аксиома о параллельных: Аксиома Лобачевского о параллельных:

выводы Изучив вопросы по данной теме мы пришли к выводам: каждый разносторонне развитый ученик должен знать историю параллельных прямых параллельные прямые часто встречаются в окружающем нас мире, поэтому они очень нужны.

выводы параллельные прямые не пересекаются на плоскости! в пространстве параллельность прямых исчезает – существует точка пересечения параллельных прямых!

. Было бы легче остановить Солнце, легче сдвинуть Землю, чем свести параллели к схождению.