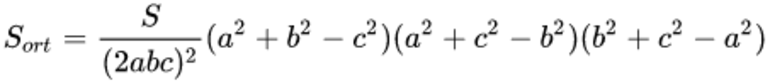Докажите что точка пересечения высот треугольника является центром вписанной окружности (6 видео)

В остроугольном треугольнике ABC проведены высоты АА1, ВВ1 и СС1. Докажите, что точка пересечения высот треугольника ABC является центром вписанной в треугольник А1В1С1 окружности.

Содержание

Ваш ответ
Похожие вопросы
Свойства высот треугольника. Ортоцентр
Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра
Что такое высота
Свойства ортоцентра
Полезные факты
Задача Фаньяно
История изучения
🎥 Видео

Видео:ОГЭ 2021 Задание 24Скачать

Ваш ответ

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

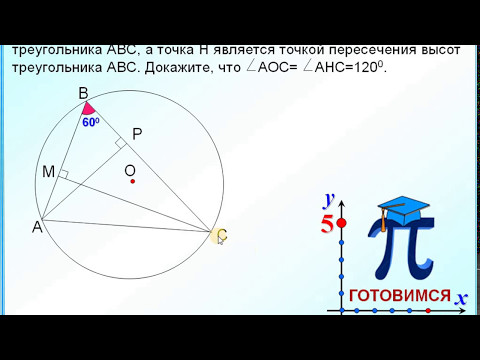
Свойства высот треугольника. Ортоцентр

Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если , и , если

Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
Четырехугольник ВКМН также можно вписать в окружность.
Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
,где R – радиус описанной окружности .

Докажем эти факты по порядку.

1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам

Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.

2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .

Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.

3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН — прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.

4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,

Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.

5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .

Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что

Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)

2. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и

а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .

— смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).

Видео:Решение задачи №30 Лазута С.Ю.Скачать

Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра

Видео:Задание 16 ЕГЭ по математикеСкачать

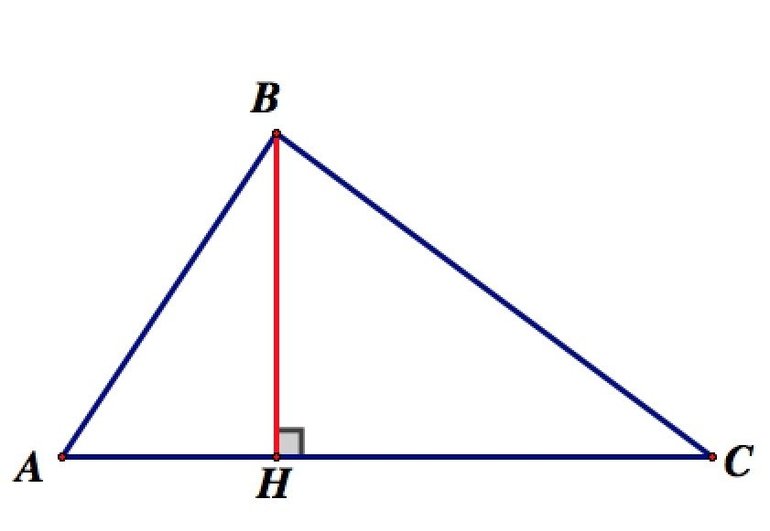
Что такое высота

Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

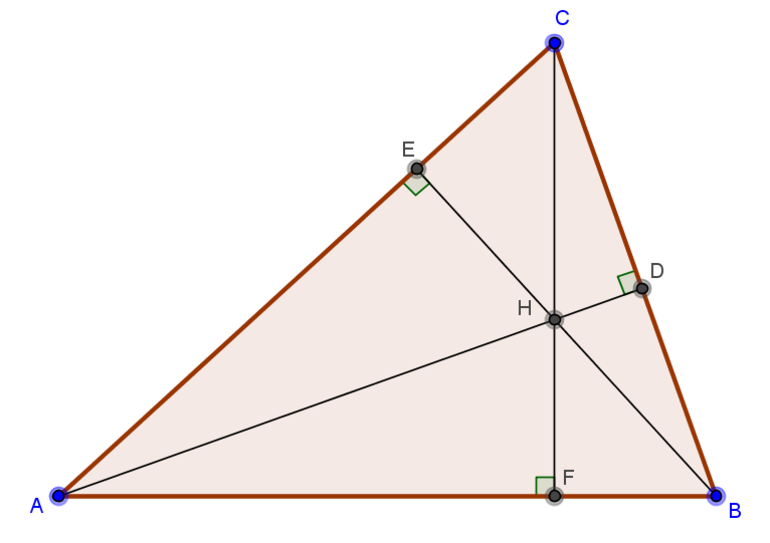
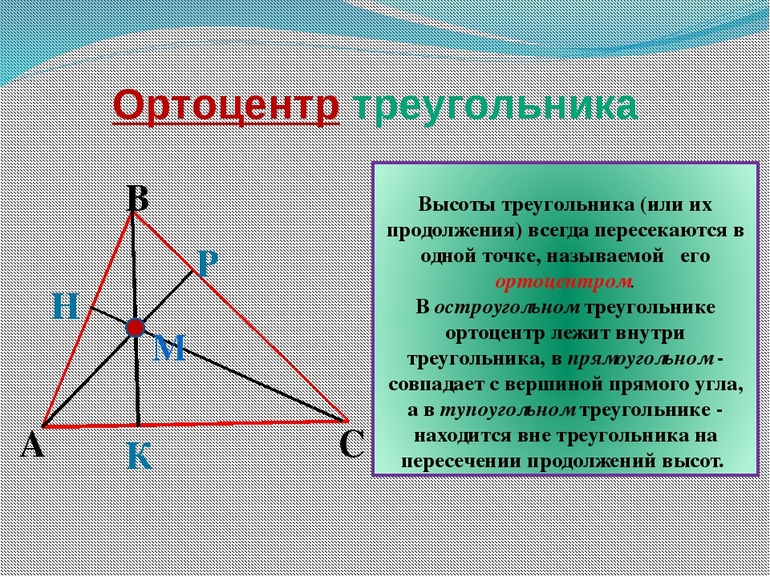
Свойства ортоцентра

Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

внутри;
снаружи;
в вершине (у прямоугольных треугольников)

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

H — ортоцентр в ABC;
О — центр описанной окружности.

Тогда:

окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
отрезок BH вдвое длиннее отрезка АС;
середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.

Площадь ортотреугольника рассчитывается по формуле:

Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

Видео:✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.