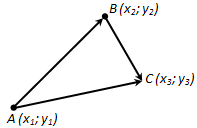- Ваш ответ
- Похожие вопросы
- Коллинеарность векторов, условия коллинеарности векторов.
- Условия коллинеарности векторов
- Примеры задач на коллинеарность векторов
- Примеры задач на коллинеарность векторов на плоскости
- Примеры задач на коллинеарность векторов в пространстве
- Докажите что для неколлинеарных векторов a и b выполняется неравенство a b
- 🌟 Видео
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Ваш ответ
Видео:№761. Докажите, что если А, В, С и D — произвольные точки, то AB + BC + CD + DA= 0.Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,989
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:№760. Докажите, что для любых двух неколлинеарных векторов х и у справедливоСкачать

Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Видео:Коллинеарные векторы.Скачать

Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | ay | . |
| bx | by |
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | . |
| bx | by |
| 3 | = | 2 | . |
| 9 | n |
Решим это уравнение:
| n = | 2 · 9 | = 6 |
| 3 |
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Видео:№776. Начертите два неколлинеарных вектора х и у и постройте векторы: a) x+2y; б) ½y + х; в) 3x+½yСкачать

Докажите что для неколлинеарных векторов a и b выполняется неравенство a b
Для доказательства достаточно сравнить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равными координатами равны.
Для доказательства достаточно сравнить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равными координатами равны.
Вопрос 13. Докажите векторное равенство (overline + overline = overline).
Ответ. Теорема 10.1. Каковы бы ни были точки A, B, C, имеет место векторное равенство
(overline + overline = overline).
Доказательство. Пусть A (x1; y1), B (x2; y2), C (x3; y3) – данные точки (рис. 215). Вектор (overline) имеет координаты x3 — x2, y3 — y2. Следовательно, вектор (overline + overline) имеет координаты x3 — x1, y3 — y1. А это есть координаты вектора (overline). Значит, векторы (overline + overline) и (overline) равны. Теорема доказана.
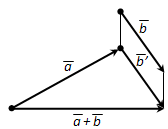
Вопрос 15. Сформулируйте «правило параллелограмма» сложения векторов.
Ответ. Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах («правило параллелограмма», рис. 217). Действительно, (overline + overline = overline), а (overline = overline). Значит, (overline + overline = overline).
Вопрос 17. Дайте определение умножения вектора на число.
Ответ. Произведением вектора (a1; a2) на число (lambda) называется вектор (overline<lambda)a1; (lambda)a2>), т.е. ((overline<a1; a2>) lambda = (overline<lambda a1; lambda a2>)).
По определению ((overline<a1; a2>) lambda = lambda (a1; a2)).
Из определения операции умножения вектора на число следует, что для любого вектора (overline) и чисел (lambda), (mu)
🌟 Видео
№752. Верно ли утверждение: а) если вектор a = вектору b, то a⇈bСкачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

№741. Начертите два неколлинеарных вектора а и b. Изобразите несколько векторов:Скачать

№801. Докажите, что для любых векторов х и у справедливы неравенства |х|-|у|≤|х + у|≤|х| + |у|.Скачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

№765. Пусть X, Y и Z— произвольные точки. Докажите, что векторы р =XY+ZXСкачать

Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

№778. Начертите попарно неколлинеарные векторы а, b и c. Постройте векторы:Скачать

89. Разложение вектора по двум неколлинеарным векторамСкачать

Равенство векторов. 9 класс.Скачать

Разложение вектора на неколлинеарные вектора.Скачать