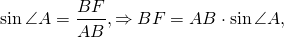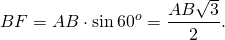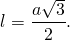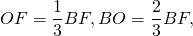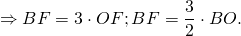В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.
Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.
Видео:№420. Докажите, что прямая, содержащая биссектрису равнобедренного треугольникаСкачать
Свойства биссектрисы равностороннего треугольника
Свойство 1
Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.
BD – биссектриса угла ABC, которая также является:
- высотой, опущенной на сторону AC;
- медианой, делящей сторону AC на два равных отрезка (AD = DC);
Свойство 2
Все три биссектрисы равностороннего треугольника равны между собой.
Свойство 3
Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.
Свойство 4
Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.
- r – радиус вписанной окружности;
- R – радиус описанной окружности;
- R = 2r.
Свойство 5
Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.
Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.
Свойство 6
Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.
- AD и AE – внешние биссектрисы, параллельные BC;
- BK и BL – внешние биссектрисы, параллельные AC;
- CM и CN – внешние биссектрисы, параллельные AB.
Свойство 7
Длину биссектрисы ( la ) равностороннего треугольника можно выразить через его сторону.
где a – сторона треугольника.
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать
Пример задачи
Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.
Решение
Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).
Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):
Видео:№233. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника,Скачать
Биссектриса равностороннего треугольника
Какими свойствами обладает биссектриса равностороннего треугольника? Как, зная сторону правильного треугольника, найти его биссектрису? Чему равна длина биссектрисы через радиус вписанной и описанной окружностей?
(свойство биссектрисы равностороннего треугольника)
В равностороннем треугольнике биссектриса, проведённая к любой стороне, является также его медианой и высотой.
Пусть в треугольнике ABC AB=BC=AC.
Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.
Проведем биссектрису BF.
По свойству равнобедренного треугольника, BF является также его медианой и высотой.
Аналогично, треугольник ABC — равнобедренный с основанием BC, треугольник ABC — равнобедренный с основанием AB, а его биссектрисы AK и CD — еще и медианы и высоты.
Что и требовалось доказать .
(свойство биссектрис равностороннего треугольника)
Все три биссектрисы равностороннего треугольника равны между собой.
Пусть в треугольнике ABC AB=BC=AC.
AK, BF CD — биссектрисы треугольника ABC.
В треугольниках ABF, BCD и CAK:
- AB=BC=CA (по условию)
- ∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника)
- ∠ABF=∠BCD=∠CAK (как как AK, BF CD — биссектрисы равных углов).
Значит, треугольники ABF, BCD и CAK равны (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AK=BF=CD.
Что и требовалось доказать .
Из теорем 1 и 2 следует, что в равностороннем треугольнике все биссектрисы, медианы и высоты равны между собой.
1) Найдём биссектрису равностороннего треугольника через его сторону.
В треугольнике ABC AB=BC=AC=a.
BF — биссектриса, BF=l.
По свойствам равностороннего треугольника, BF — высота ∆ ABC, ∠A=60º.
Из прямоугольного треугольника ABF по определению синуса
Таким образом, формула биссектрисы равностороннего треугольника по его стороне:
2) Найдём биссектрису равностороннего треугольника через радиусы вписанной и описанной окружностей.
В правильном треугольнике ABC центры вписанной и описанной окружностей совпадают.
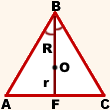
Центр вписанной окружности — точка пересечения биссектрис треугольника. Биссектрисы равностороннего треугольника также являются его медианами. Медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины.
Следовательно, точка O — центр вписанной и описанной окружностей, OF — радиус вписанной окружности, OF=r, BO — радиус описанной окружности, BO=R и BO:OF=2:1.
Таким образом, длина биссектрисы через радиус вписанной окружности равна
Видео:№225. Докажите, что каждый угол равностороннего треугольника равен 60°.Скачать
Теорема о биссектрисе треугольника. Доказательство
Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:
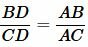 | (1) |
 |
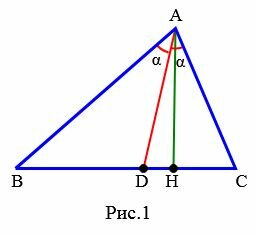Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:
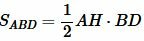 , | (3) |
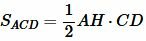 . | (4) |
Построим следующее соотношение
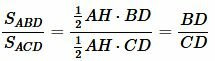 . | (5) |
С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:
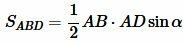 . | (6) |
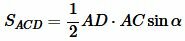 . | (7) |
Построим следующее соотношение используя формулы (6) и (7):
 . | (8) |
Из формул (5) и (8) получим соотношение (1).
Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).
 |
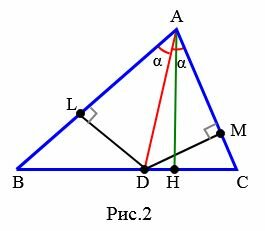Тогда площади треугольников ABD и ACD можно найти из формул:
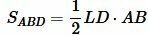 , | (9) |
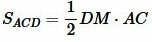 . | (10) |
Построим следующее соотношение
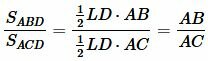 . | (11) |
Из формул (5) и (11) получим соотношение (1).
Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):
 |
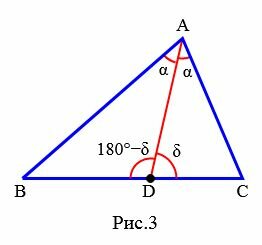Применяя теорему синусов для треугольников ABD и ACD можем записать:
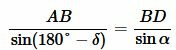 , | (12) |
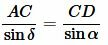 . | (13) |
Поделив (12) на (13) и учитывая, что ( small sin(180°-delta)=sin delta , ) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1).
Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.
 |
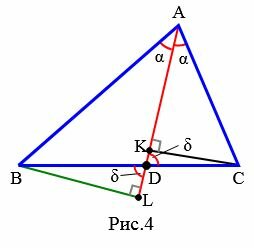Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (( small ∠ ALB= ∠ AKC ,;; ∠ BAL= ∠ CAK ) ). Тогда имеем:
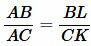 | (14) |
Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку ( small ∠ BLD= ∠ CKD ,) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:
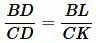 | (15) |
Из равенств (14) и (15) получаем:
 . |
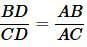Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.
Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:
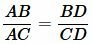 . | (16) |
Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:
 |
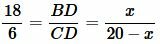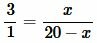 . | (17) |
Методом перекресного умножения упростим (17) и решим:
💥 Видео
№133. Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольникСкачать
Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать
Свойство биссектрисы треугольника с доказательствомСкачать
Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать
Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать
Формулы равностороннего треугольника #shortsСкачать
Равнобедренный треугольник. 7 класс.Скачать
Высота, биссектриса, медиана. 7 класс.Скачать
Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать
№135. Докажите, что если сторона одного равностороннего треугольника равна стороне другогоСкачать
Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать
Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать
Геометрия Равносторонний треугольникСкачать
Теорема о свойстве медианы равнобедренного треугольникаСкачать
3 свойства биссектрисы #shortsСкачать
ПОМОГИТЕ ДОКАЗАТЬ Если две биссектрисы равны, то треугольник равнобедренныйСкачать
