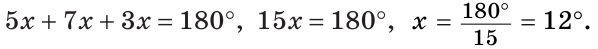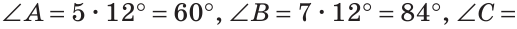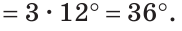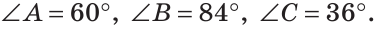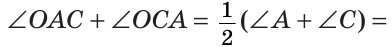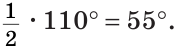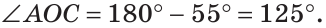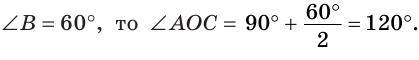Наглядная геометрия 7 класс. Опорный конспект № 4 Сумма углов треугольника.
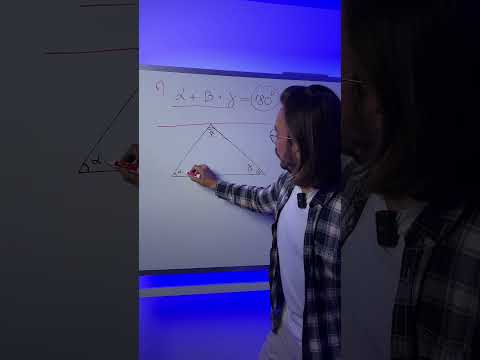
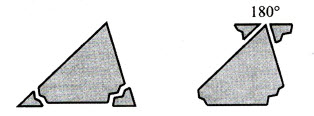
Великий французский ученый XVII века Блез Паскаль в детстве любил возиться с геометрическими фигурами. Он был знаком с транспортиром и умел измерять углы. Юный исследователь заметил, что у всех треугольников сумма трех углов получается одна и та же — 180°. «Как же это доказать? — подумал Паскаль. — Ведь нельзя же проверить сумму углов у всех треугольников — их бесконечное множество». Тогда он отрезал ножницами два уголка треугольника и приложил их к третьему углу. Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие. Дальнейшая судьба мальчика была уже предопределена.
В этой теме вы познакомитесь с пятью признаками равенства прямоугольных треугольников и, пожалуй, с самым популярным свойством прямоугольного треугольника с углом 30°. Оно звучит так: катет, лежащий против угла 30°, равен половине гипотенузы. Разделив равносторонний треугольник высотой, мы сразу получим доказательство этого свойства.
Сумма углов треугольника
ТЕОРЕМА. Сумма углов треугольника равна 180°. Для доказательства проведем через вершину прямую, параллельную основанию. Темные углы равны и серые углы равны как накрест лежащие при параллельных прямых. Темный угол, серый угол и угол при вершине образуют развернутый угол, их сумма 180°. Из теоремы следует, что углы равностороннего треугольника равны по 60° и что сумма острых углов прямоугольного треугольника равна 90°.
Внешним углом треугольника называется угол, смежный с углом треугольника. Поэтому иногда углы самого треугольника называют внутренними углами.
ТЕОРЕМА о внешнем угле треугольника. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним. Действительно, внешний угол и два внутренних, не смежных с ним, дополняют закрашенный угол до 180°. Из теоремы следует, что внешний угол больше любого внутреннего, не смежного с ним.
ТЕОРЕМА о соотношениях между сторонами и углами треугольника. В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона. Отсюда следует: 1) Катет меньше гипотенузы. 2) Перпендикуляр меньше наклонной.
Расстояние от точки до прямой. Так как перпендикуляр меньше любой наклонной, проведенной из той же точки, то его длина принимается за расстояние от точки до прямой.
Неравенство треугольника. Длина любой стороны треугольника меньше суммы двух других его сторон, т. е. а
ТЕОРЕМА о свойстве катета, лежащего против угла 30°. Катет, лежащий против угла 30°, равен половине гипотенузы. Доказывается достроением треугольника до равностороннего.
ТЕОРЕМА о свойстве точек биссектрисы угла. Любая точка биссектрисы угла равноудалена от его сторон. Если точка равноудалена от сторон угла, то она лежит на биссектрисе угла. Доказывается проведением двух перпендикуляров к сторонам угла и рассмотрением прямоугольных треугольников.
Вторая замечательная точка. Биссектрисы треугольника пересекаются в одной точке.
Расстояние между параллельными прямыми. ТЕОРЕМА. Все точки каждой из двух параллельных прямых находятся на равном расстоянии от другой прямой. Из теоремы следует определение расстояния между параллельными прямыми.
Определение. Расстоянием между двумя параллельными прямыми называется расстояние от любой точки одной из параллельных прямых до другой прямой.
Подробные доказательства теорем


Это опорный конспект № 4 по геометрии в 7 классе «Сумма углов треугольника». Выберите дальнейшие действия:
Видео:ПОЧЕМУ СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180? #shorts #геометрия #егэ #огэ #треугольникСкачать

Сумма углов треугольника
Сумма треугольника равна 180 градусов.
Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.
А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение
2. Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны .
3. На рисунке угол равен , угол равен , угол равен . Найдите угол . Ответ дайте в градусах.
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Сначала найдем угол .
Угол , смежный с углом равен .
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Ты нашел то, что искал? Поделись с друзьями!
4. Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.
Пусть углы треугольника равны , и . Запишем, чему равна сумма углов этого треугольника.
Как же все-таки доказать, что сумма углов треугольника равна 180 градусов? Очень просто. На нашем рисунке угол равен углу (они накрест лежащие). Угол равен углу (тоже накрест лежащие). Развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
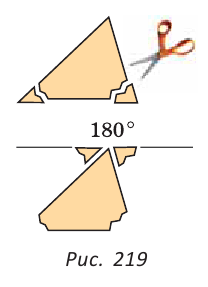
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 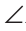
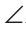
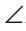
Доказательство:
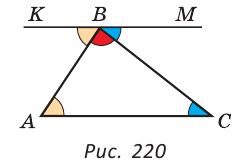
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 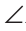
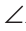
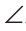
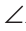
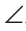





Следствия.
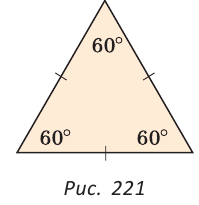
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
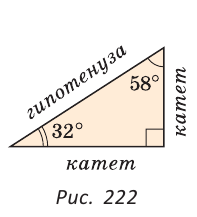
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
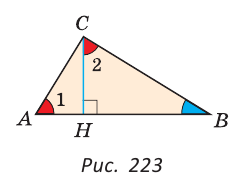
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
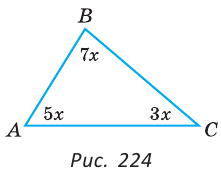
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 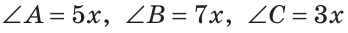
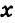
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
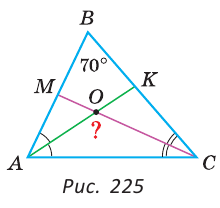
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 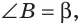
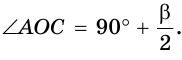
Пример:
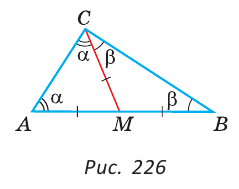
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 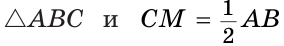
Докажем, что

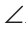






















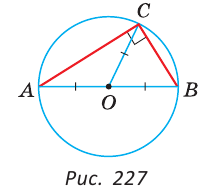
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
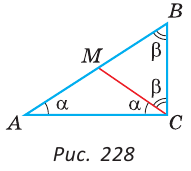
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Сумма углов треугольника. Доказательство теоремы о сумме углов треугольника. Геометрия 7 класс.Скачать

Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Почему сумма углов треугольника 180 градусов?Скачать

Сумма углов 180 градусовСкачать

СУММА УГЛОВ ТРЕУГОЛЬНИКА 180 градусовСкачать

А ты знал? Почему сумма углов треугольника 180 градусов. #математика #геометрия #углы #7классСкачать

Сумма углов треугольника равна 180Скачать

Почему сумма углов в треугольнике равна 180 градусовСкачать
Внешний угол треугольникаСкачать

Сумма углов треугольникаСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Теорема 14.2 Если сумма односторонних углов равна 180 градусов, то прямые параллельны || Геометрия 7Скачать

Сумма углов треугольникаСкачать

31. Теорема о сумме углов треугольникаСкачать

Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Почему сумма углов треугольника 180 градусов? 📚 #егэ #профильнаяматематика #профиль #егэпрофильСкачать